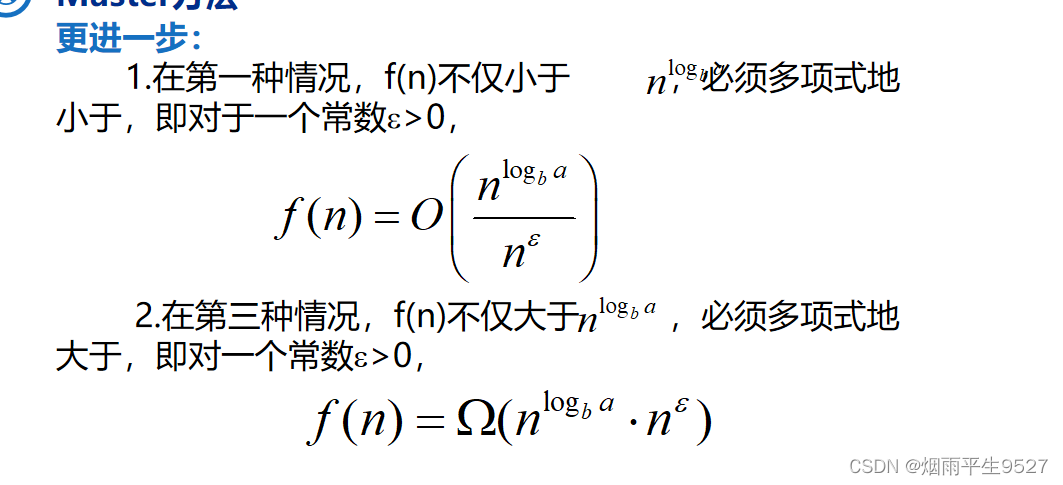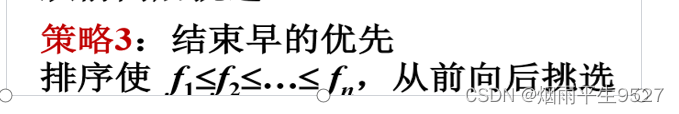算法的世界就像一场解谜游戏，而每种算法都是我们手中的解谜钥匙。比如，分治法就是“分而治之”，把一个大问题拆分成小问题，逐一解决，再合并答案，就像把一块大蛋糕切成小块分给朋友。动态规划则是“记忆高手”，它会记录每次解决的小问题，避免重复计算，省时又省力。贪心算法则是“短视的天才”，它每一步都选择当前最优解，虽然可能看不到全局，但往往能快速解决问题。比如在排队时，贪心算法会选择先让时间短的人先走，这样整体等待时间最少。你可能会问：“为什么分治法效率高？”这是因为分治法通过递归减少问题规模，把大问题变成小问题，就像切蛋糕一样，每一块都更容易处理。下次遇到复杂问题，不妨想想这些算法，或许会让你的生活更高效哦！

前言：基本是为了我自己看的一些我容易忘记的东西，为考试作准备把

第一章

算法中的基本概念

程序设计=数据结构+算法

算法特性

1.有穷性

2.确定性

3.可行性

4.输出

5.输入

算法复杂性分析

算法复杂性依赖于：问题规模N，输入I，算法本身A

时间复杂性T和空间复杂性S

时间复杂度

1.Master定理

求解T(n)=aT(n/b)+f(n)型方程，

第二章

递归算法：直接或者间接调用自身的算法称为递归算法

分治法的基本步骤如下：

1. 分解：将原问题分解为若干个规模较小的子问题，这些子问题相互独立且与原问题形式相同。
2. 解决：递归地解决各个子问题。如果子问题的规模足够小，则直接解决。
3. 合并：将各个子问题的解合并起来，构成原问题的解。

Strassen矩阵乘法：

1. 问题描述：给定两个n*n的矩阵A B，求C=A*B;

改进：

第三章

动态规划通常用于解决具有重叠子问题和最优子结构的问题。

动态规划的基本步骤如下：

1. 定义状态：定义一个状态数组，用于存储子问题的解。
2. 状态转移方程：定义状态转移方程，用于描述如何从一个状态转移到另一个状态。
3. 初始化：初始化状态数组中的某些值。
4. 计算结果：根据状态转移方程和初始值，计算状态数组中的所有值，最终得到原问题的解。

备忘录方法        自顶向下的递归方式

动态规划算法        以自底向上

贪心算法以自顶向下的方式进行

第四章

贪心法是一种解决问题的方法，它在每一步都选择当前看起来最优的解，希望最终得到全局最优解。贪心法通常用于解决具有贪心选择性质和最优子结构的问题。

贪心法的基本步骤如下：

1. 定义目标函数：定义一个目标函数，用于衡量解的优劣。
2. 贪心选择：在每一步中，选择当前看起来最优的解。
3. 证明正确性：证明贪心选择能够得到全局最优解。

贪心选择性        最优子结构

贪心法的适用范围

贪心策略适用的前提是：局部最优策略能导致产生全局最优解。

选择题填空题

程序设计=数据结构+算法

算法分析

 大整数乘法：

1. 问题描述：n位10进制整数X和Y,输出X和Y的乘积；

棋盘覆盖问题：

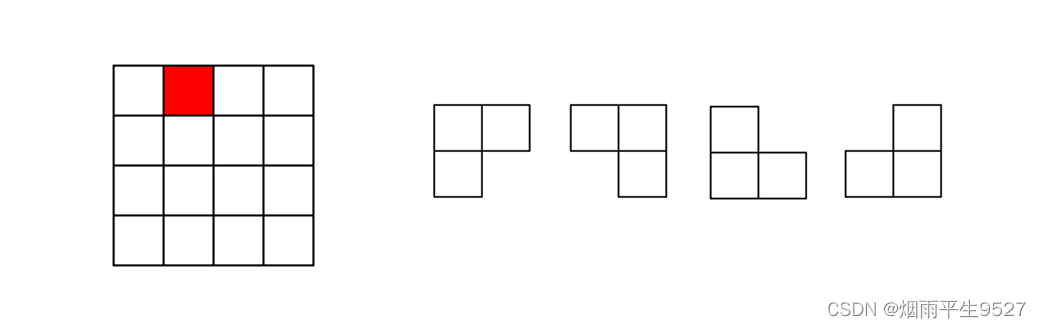
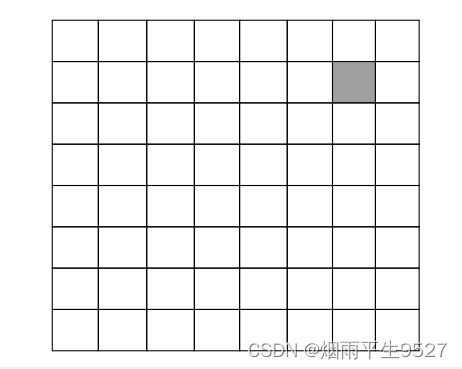
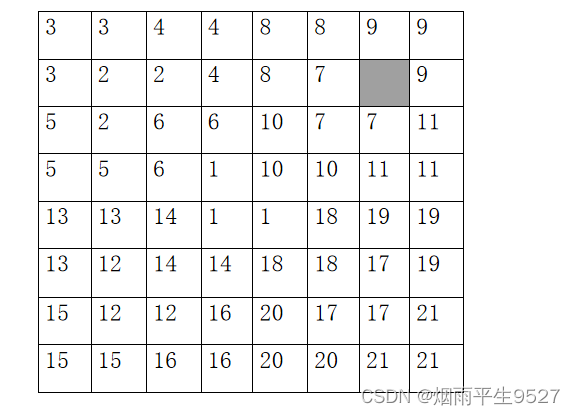
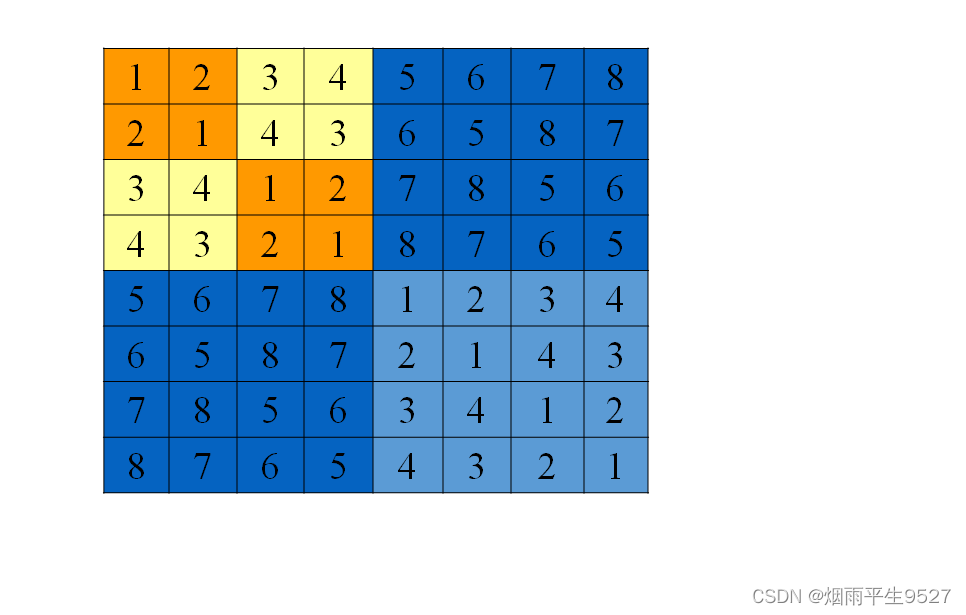
1. 问题描述：在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在 棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格， 且任何2个L型骨牌不得重叠覆盖。

具体思想就是将一个大棋盘分割成4个小棋盘，有3个小棋盘中没有特殊方格，用一个L型的骨牌覆盖3个小棋盘的汇合处。按照左上、右上、左下、右下的方法递归覆盖。

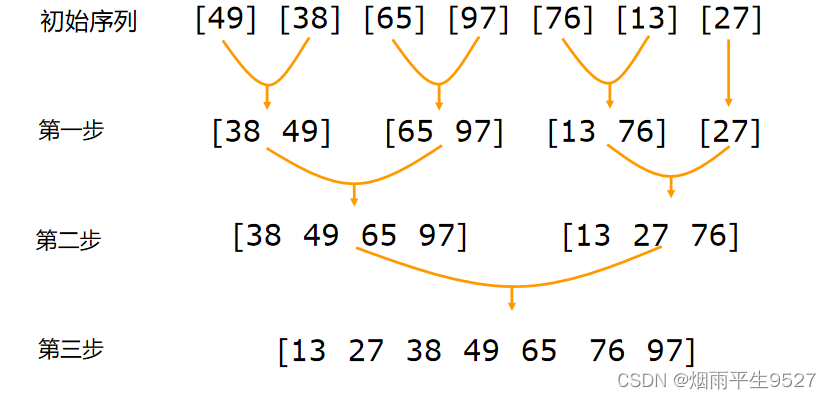
合并排序

改进 

 

循环赛日程表：

 

矩阵连乘

最长公共子序列问题

思路 

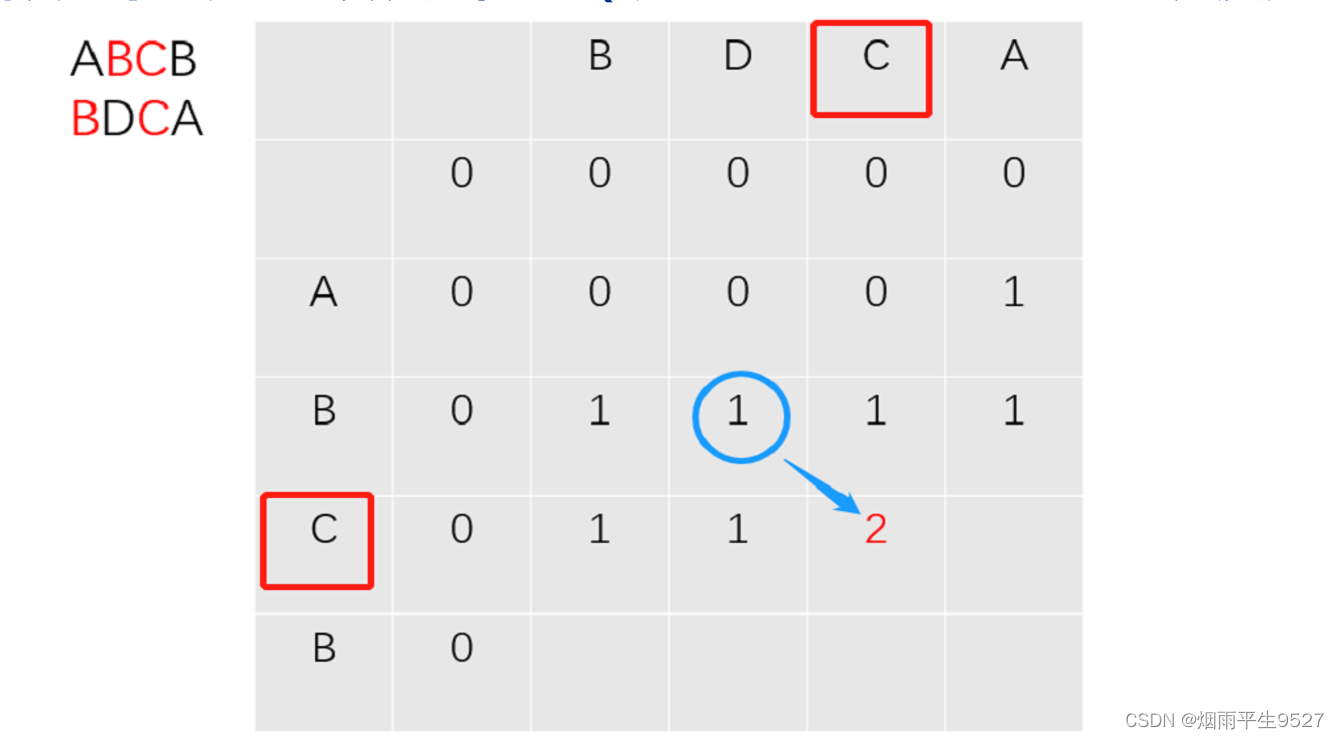
 追踪

 

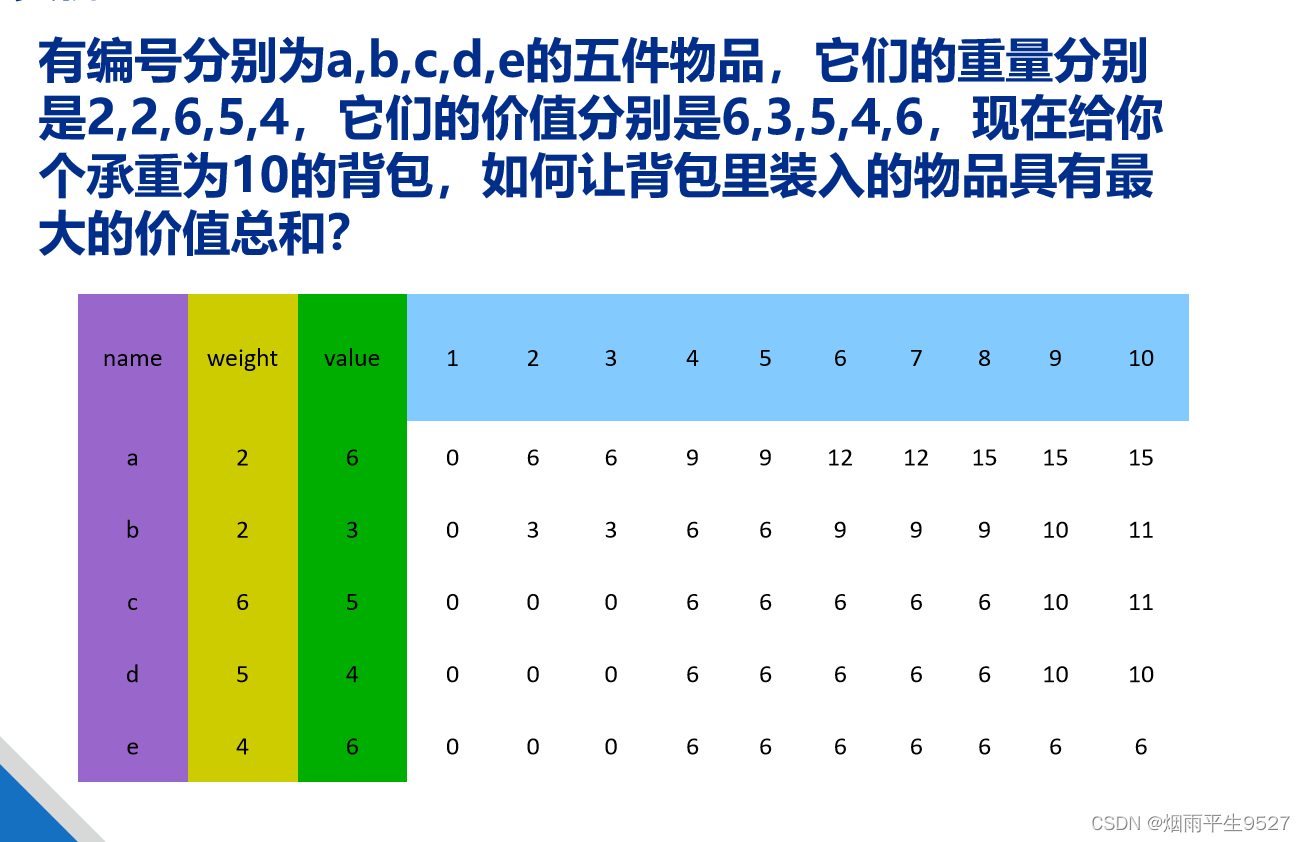
0-1背包

 

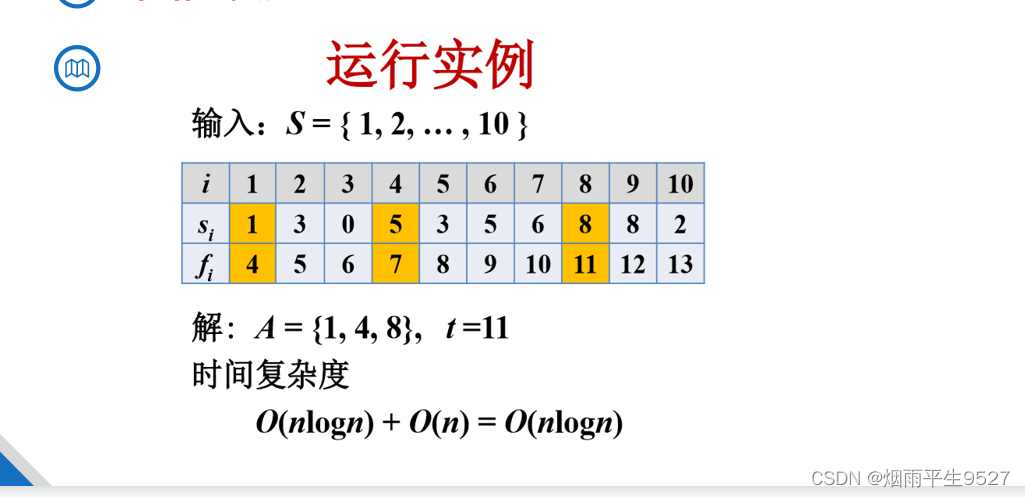
活动安排问题

 

 

程序设计

汉诺塔问题

问题描述：Hanoi问题起源于一个类似传说故事，在Hanoi这个地方有一个寺庙，这里有3根柱子和64个大小不同的金碟子。每个碟子有一个孔可以穿过。所有的碟子都放在第一个柱子上，而且按照从上到下碟子的大小依次增大的顺序摆设。如下图所示。现在，假定寺庙里的僧侣要移动这些碟子，将它们从柱子a移动到柱子b上。不过移动的规则如下：    1.每次只能从一个柱子的最上面移动一个碟子到另外一个柱子上。    2.不能将大碟子放到小碟子的上面。    按照前面这个规则，我们该怎么去移动这些碟子呢？

void hanoi(int n,char a,char b,char c)//将n个碟子从a移到b{ if(n==0) return; else { hanoi(n-1,a,c,b); move(a,b); hanoi(n-1,c,b,a);｝
｝

• 移动方法是从a->b->c->a，在移动圆盘的时候，若是奇数次移动，则将最小的圆盘移动到顺时针方向的下一个塔座上，若是偶数次移动，则在其他两个塔座之间，将较小的圆盘移动到另一个塔座上去；

全排序

void Perm(int list[], int k, int m)
{if(k==m){   for(int i=0;i<=m;i++)   cout<<list[i];cout<<endl;}elsefor(int i=k;i<=m;i++){  swap(list[k],list[i]);Perm(list, k+1,m);swap(list[k],list[i]);} }

快速排序

#include<algorithm>#include<cstdio>using namespace std;const int N=1e5+5;int q[N];void quick_sort(int *q,int l,int r){if(l>=r)