剑指 Offer —— 数组和字符串

剑指 Offer 04. 二维数组中的查找

在一个 n * m 的二维数组中：

• 每一行都按照从左到右 非递减 的顺序排序
• 每一列都按照从上到下 非递减 的顺序排序
  请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

• 现有矩阵 matrix 如下：

[[1,   4,  7, 11, 15],[2,   5,  8, 12, 19],[3,   6,  9, 16, 22],[10, 13, 14, 17, 24],[18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。
给定 target = 20，返回 false

限制：
0 <= n <= 1000
0 <= m <= 1000

代码实现

class Solution:def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:row=len(matrix)-1col=0while( row>=0 and col<len(matrix[0]) ):if(matrix[row][col]==target):return Trueelse:if(matrix[row][col]>target):row=row-1else:col=col+1return False

解题方案 + 思路

• 标签：数组遍历
• 从矩阵的左下角看，上方的数字都比其小，右方的数字都比其大，所以依据该规律去判断数字是否存在
  • 设当前数字为 cur，目标数字为 target
    • 当 target < cur 时，cur 更新为其上面的数字
    • 当 target > cur 时，cur 更新为其右侧的数字
  • 直到相等则返回 true，否则到了矩阵边界返回 false
• 时间复杂度：O(m+n)

算法步骤

其他实现思路——二分查找

• 看到有序，第一反应就是二分查找。最直接的做法，一行一行的进行二分查找即可。

此外，结合有序的性质，一些情况可以提前结束。

• 比如某一行的第一个元素大于了 target ，当前行和后边的所有行都不用考虑了，直接返回 false。
• 某一行的最后一个元素小于了 target ，当前行就不用考虑了，换下一行。

本题没有确保「每行的第一个整数大于前一行的最后一个整数」，因此我们无法采取「两次二分」的做法。

• 只能退而求之，遍历行/列，然后再对列/行进行二分。

时间复杂度的话，如果是 m 行 n 列，就是 O(mlog(n))。

import numpy as npclass Solution(object):def searchMatrix(self, matrix, target):""":type matrix: List[List[int]]:type target: int:rtype: bool"""matrix = np.array(matrix)row = matrix.shape[0]col = matrix.shape[1]flag =0for row in matrix:left = 0right = col-1while(left<=right):mid = (left+right+1)/2if row[mid]<target:left=mid+1elif row[mid]>target:right=mid-1else:return Truereturn False

其他实现思路_变形的二分法

二分法的思想就是，目标值和中点值进行比较，然后可以丢弃一半的元素。

• 这道题的话是矩阵
• 如果我们找到矩阵的中心，然后和目标值比较看能不能丢弃一些元素。

如下图，中心位置是 9
[1,   4,  7, 11, 15],
[2,   5,  8, 12, 19],
[3,   6, /9/,16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]通过中心位置, 我们可以把原矩形分成四个矩形, 左上, 右上, 左下, 右下
[1,   4,  7   [11, 15  2,   5,  8    12, 19  3,   6, /9/]  16, 22] [10, 13, 14   [17, 24
[18, 21, 23]   26, 30]如果 target = 10,
此时中心值小于目标值，左上角矩形中所有的数都小于目标值，我们可以丢弃左上角的矩形，继续从剩下三个矩形中寻找如果 target = 5,
此时中心值大于目标值，右下角矩形中所有的数都大于目标值，那么我们可以丢弃右下角的矩形，继续从剩下三个矩形中寻找

我们找到了丢弃元素的原则，可以写代码了。

这里的话，矩形我们用左上角和右下角坐标的形式表示，下图是分割后矩形的坐标情况。

我们可以用递归的形式去写，

• 递归出口的话，当矩阵中只有一个元素，直接判断当前元素是不是目标值即可。

还有就是分割的时候可能越界，

• 比如原矩阵只有一行，左下角和右下角的矩阵其实是不存在的，
• 按照上边的坐标公式计算出来后，我们要判断一下是否越界。

剑指 Offer 05. 替换空格

题目描述

请实现一个函数，把字符串 s 中的每个空格替换成 “%20”。

示例 1：

• 输入：s = “We are happy.”
• 输出：“We%20are%20happy.”

限制：
0 <= s 的长度 <= 10000

代码实现

Python简单法：

class Solution:def replaceSpace(self, s: str) -> str:return "%20".join(s.split(' '))

Python法：

class Solution {
public:string replaceSpace(string s) {for(int i = 0; i < s.length(); i++){if(s.find(" ") == i){s.erase(i, 1);s.insert(i, "%20");}}return s;}
};

class Solution(object):def replaceSpace(self, s):""":type s: str:rtype: str"""s1=""for c in s:if c == ' ': s1 += '%20'else:s1 +=creturn s1

C++:

class Solution {
public:string replaceSpace(string s) {for(int i = 0; i < s.length(); i++){if(s.find(" ") == i){ # 查找到空格所在的位置s.erase(i, 1); # 先清除空格所占的一个字符s.insert(i, "%20"); # 在该位置插入%20}}return s;}
};

解题方案 + 思路

• 标签：字符串
• 最简单的方案自然是直接使用库函数啦！当然题目肯定是不希望我们这样做的！
• 增加一个新字符串，遍历原来的字符串，遍历过程中，
  • 如果非空格则将原来的字符直接拼接到新字符串中
  • 如果遇到空格则将%20拼接到新字符串中
• 时间复杂度：O(n)，空间复杂度：O(n)

算法步骤

方法总结

法一：遍历添加
在 Python 和 Java 等语言中，字符串都被设计成「不可变」的类型，即无法直接修改字符串的某一位字符，需要新建一个字符串实现。

算法流程：

1. 初始化一个 list (Python) / StringBuilder (Java) ，记为 res ；
2. 遍历列表 s 中的每个字符 c ：
   • 当 c 为空格时：向 res 后添加字符串 "%20" ；
   • 当 c 不为空格时：向 res 后添加字符 c ；
3. 将列表res 转化为字符串并返回。

复杂度分析：

• 时间复杂度 O(N) ： 遍历使用 O(N) ，每轮添加（修改）字符操作使用 O(1) ；
• 空间复杂度 O(N)： Python 新建的 list 和 Java 新建的 StringBuilder 都使用了线性大小的额外空间。

方法二：原地修改
在 C++ 语言中， string 被设计成「可变」的类型（参考资料），因此可以在不新建字符串的情况下实现原地修改。

• 由于需要将空格替换为 “%20” ，字符串的总字符数增加，因此需要扩展原字符串 s 的长度，
• 计算公式为：新字符串长度 = 原字符串长度 + 2 * 空格个数 ，
• 示例如下图所示。
  
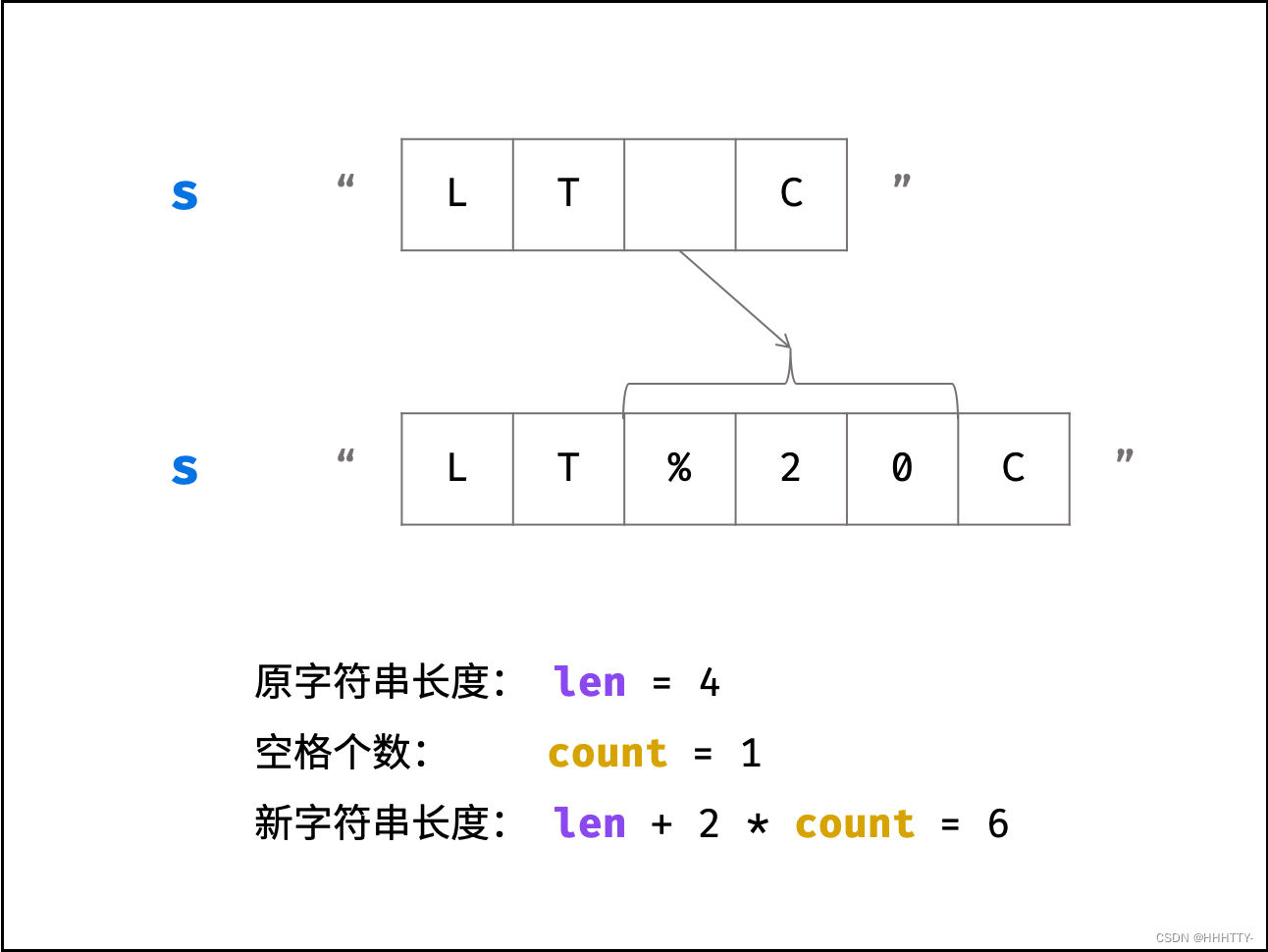
  算法流程：

1. 初始化：空格数量 count ，字符串 s 的长度 len ；
2. 统计空格数量：遍历 s ，遇空格则 count++ ；
3. 修改 s 长度：添加完 “%20” 后的字符串长度应为 len + 2 * count ；
4. 倒序遍历修改：i 指向原字符串尾部元素， j 指向新字符串尾部元素；
   • 当 i = j 时跳出（代表左方已没有空格，无需继续遍历）；
   • 当 s[i] 不为空格时：执行 s[j] = s[i] ；
   • 当 s[i] 为空格时：将字符串闭区间[j-2, j]的元素修改为 "%20" ；由于修改了 3 个元素，因此需要 j -= 2 ；
5. 返回值：已修改的字符串 s ；

复杂度分析：

• 时间复杂度 O(N) ： 遍历统计、遍历修改皆使用 O(N)时间。
• 空间复杂度 O(1)： 由于是原地扩展 s 长度，因此使用 O(1)额外空间。

class Solution {
public:string replaceSpace(string s) {int count = 0, len = s.size();// 统计空格数量for (char c : s) {if (c == ' ') count++;}// 修改 s 长度s.resize(len + 2 * count);// 倒序遍历修改for(int i = len - 1, j = s.size() - 1; i < j; i--, j--) {if (s[i] != ' ')s[j] = s[i];else {s[j - 2] = '%';s[j - 1] = '2';s[j] = '0';j -= 2;}}return s;}
};

剑指 Offer 11. 旋转数组的最小数字 - 解决方案

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

• 输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。
• 例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。
• 注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：

• 输入：[3,4,5,1,2]
• 输出：1

示例 2：

• 输入：[2,2,2,0,1]
• 输出：0

提示：

• n == numbers.length
• 1 <= n <= 5000
• -5000 <= numbers[i] <= 5000
• numbers 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

代码实现

• python遍历

class Solution:def minArray(self, numbers: List[int]) -> int:j=numbers[0]for i in range(len(numbers)):if j<=numbers[i]:j=jelse:j=numbers[i]return j

• 二分法

class Solution:def findMin(self, nums: List[int]) -> int:left, right = 0, len(nums) - 1while left < right:mid = (left + right) // 2if nums[mid] > nums[right]: left = mid + 1elif nums[mid] < nums[right]: right = midelse: right = right - 1 # keyreturn nums[left]

解题方案 + 思路

• 标签：二分查找
• 整体思路：
  • 首先数组是一个有序数组的旋转，从这个条件可以看出，数组是有大小规律的，
  • 可以使用二分查找利用存在的规律快速找出结果
• 时间复杂度：O(logn)，空间复杂度：O(1)

算法步骤

1. 初始化下标 left 和 right
2. 每次计算中间下标 mid = (right + left) / 2​，这里的除法是取整运算，不能出现小数

• 当 numbers[mid] < numbers[right] 时，说明最小值在 ​[left, mid]​ 区间中，则令 right = mid，用于下一轮计算
• 当 numbers[mid] > numbers[right]​ 时，说明最小值在 [mid, right]​ 区间中，则令 left = mid + 1，用于下一轮计算
• 【注意】当 numbers[mid] == numbers[right]​ 时，无法判断最小值在哪个区间之中，此时让 right--，缩小区间范围，在下一轮进行判断

为什么是 right-- 缩小范围，而不是 left++？

• 因为数组是升序的，所以最小值一定靠近左侧，而不是右侧
• 比如，当存在 [1,2,2,2,2] 这种情况时，left = 0，right = 4，mid = 2，数值满足 numbers[mid] == numbers[right] 这个条件，如果 left++，则找不到最小值

算法思路（二分）

• 旋转排序数组 nums可以被拆分为 2 个排序数组 nums1 , nums2，并且 nums1任一元素 >= nums2任一元素；因此，考虑二分法寻找此两数组的分界点 nums[i] (即第 2 个数组的首个元素)。
• 设置 left, right 指针在 nums数组两端，mid为每次二分的中点：
  • 当 nums[mid] > nums[right]时，mid一定在第 1 个排序数组中，iii 一定满足 mid < i <= right，因此执行 left = mid + 1；
  • 当 nums[mid] < nums[right] 时，mid 一定在第 2 个排序数组中，iii 一定满足 left < i <= mid，因此执行 right = mid；
  • 当 nums[mid] == nums[right] 时，是此题对比 153题 的难点（原因是此题中数组的元素可重复，难以判断分界点 iii 指针区间）；
    • 例如 [1,0,1,1,1]，在 left = 0, right = 4, mid = 2 时，无法判断 midmidmid 在哪个排序数组中。
    • 我们采用 right = right - 1 解决此问题，证明：
      1. 此操作不会使数组越界：因为迭代条件保证了 right > left >= 0；
      2. 此操作不会使最小值丢失：假设 nums[right] 是最小值，有两种情况：
         • 若 nums[right]是唯一最小值：那就不可能满足判断条件 nums[mid] == nums[right]，因为 mid < right（left != right 且 mid = (left + right) // 2 向下取整）；
         • 若 nums[right]不是唯一最小值，由于 mid < right 而 nums[mid] == nums[right]，即还有最小值存在于 [left,right−1] 区间，因此不会丢失最小值。

以上是理论分析，可以代入以下数组辅助思考：
[1,2,3]
[1,1,0,1]
[1,0,1,1,1]
[1,1,1,1]

• 时间复杂度 O(logN)，在特例情况下会退化到 O(N)（例如 [1,1,1,1]）。

剑指 Offer 17. 打印从 1 到最大的 n 位数

题目描述

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。

• 比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

• 输入: n = 1
• 输出: [1,2,3,4,5,6,7,8,9]

说明：

• 用返回一个整数列表来代替打印
• n 为正整数

解题方案

思路 1

标签：数组
整体思路：

1. 首先求出要打印的数字范围，
2. 然后再从 1 开始打印到最大的数字
   时间复杂度：O(10n10 ^n10n )，空间复杂度：O(10n10 ^n10n )

算法流程

1. 初始化 sum = 1
2. 循环遍历乘 10 让 sum 变为边界值
3. 新建 res 数组，大小为 sum-1
4. 从 1 开始打印，直到 sum-1 为止

思路 2

标签：字符串
整体思路：

• 原题的题意其实是希望考察大数计算，因为 int 数组有可能会溢出，所以用字符串处理可以保证一定不会溢出，
• 但是呢，由于返回值规定是 int 数组，所以其实从返回值上来看，是一定不会溢出的，比较矛盾。
• 所以给出个思路 2，学习下如何用字符串处理大数即可，不用特别纠结溢出这件事情
  时间复杂度：O(10n10 ^n10n )，空间复杂度：O(10n10 ^n10n )

算法流程

1. 初始化字符串 str，另其初始值为 n-1 个 "0"
2. 递增 str，使用字符去递增
   • 递增过程中判断是否存在进位，存在进位则进位处 +1，
   • 直到达到最大值为止，结束循环
3. 每获取到一个值之后，遍历前方多余的 “0”，将多余的 “0” 去掉
   • 转换为 int 存到结果数组中