「计算机控制系统」4. 计算机控制系统分析

Z平面
稳定性分析
稳态误差分析
动态过程分析
频率特性
文章目录
- Z平面与S平面的映射关系
- 稳定性分析
-
- 离散Routh判据
- Jury判据
- 离散Nyquist判据
- 稳态误差
-
- 静态误差系数
- 动态过程
- 频率特性
Z平面与S平面的映射关系

-
S平面虚轴的映射

-
ω\\omegaω与θ\\thetaθ的映射

可以看出从S平面到Z平面并不是一一映射 -
主带与旁带

S平面上宽度ωs\\omega_sωs的一条可以映射到整个Z平面,具体的情况如下: -
主带的映射
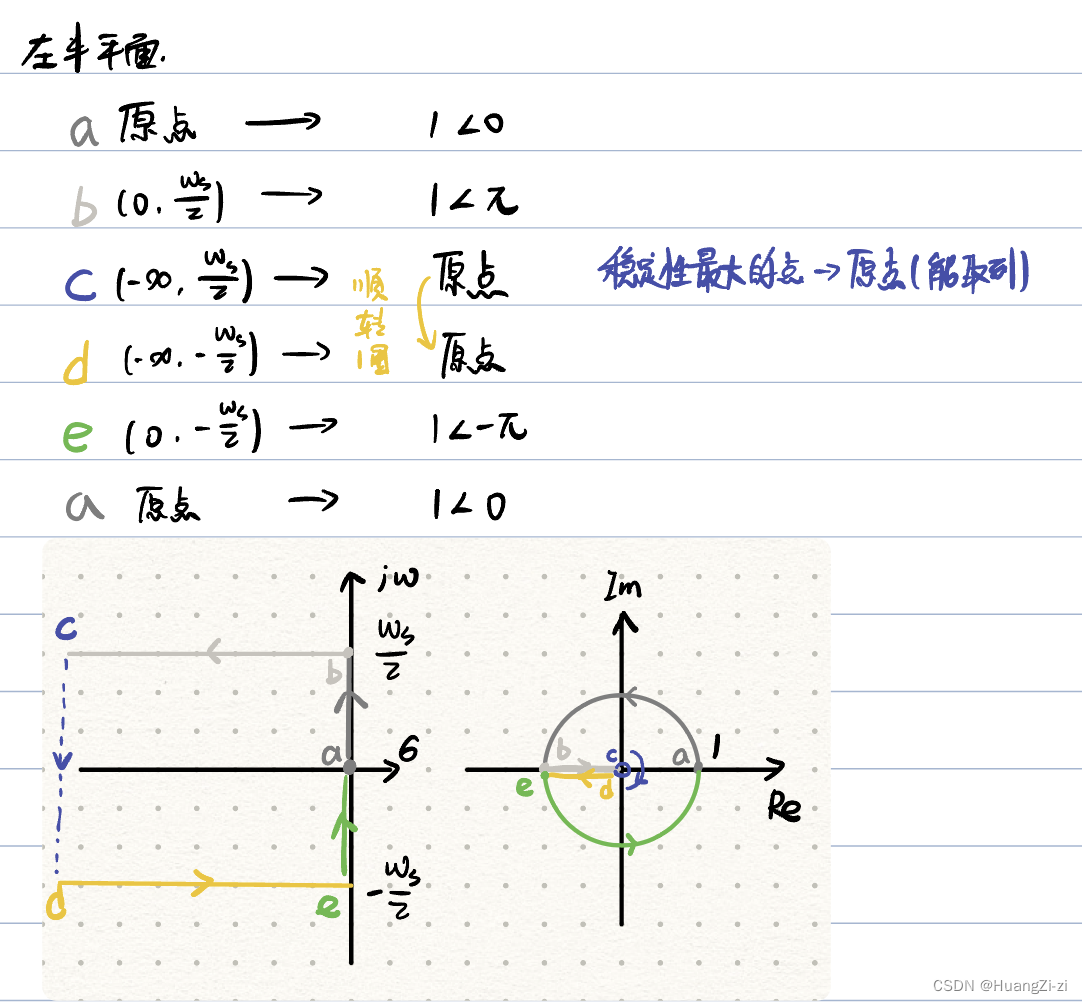
S平面主带左半平面可以映射到Z平面单位圆内。
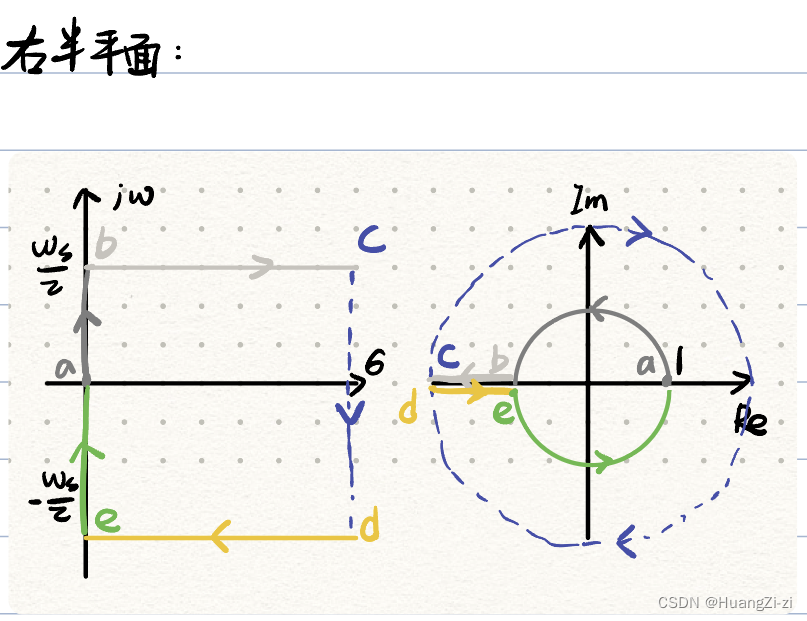
右半平面可以映射到Z平面单位圆外。 -
等频率线的映射
等频率即ω\\omegaω为常数,在S平面与实轴平行
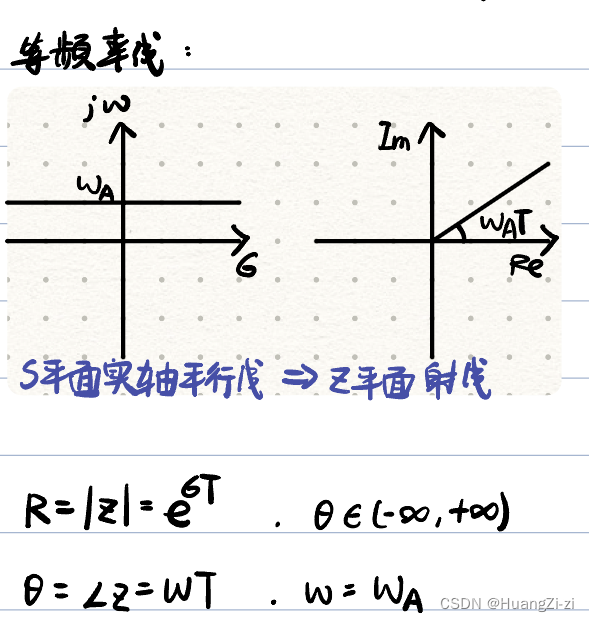
-
等衰减率线的映射
等衰减率即是ξωn\\xi \\omega_nξωn乘积为定值,对应平行于虚轴的直线
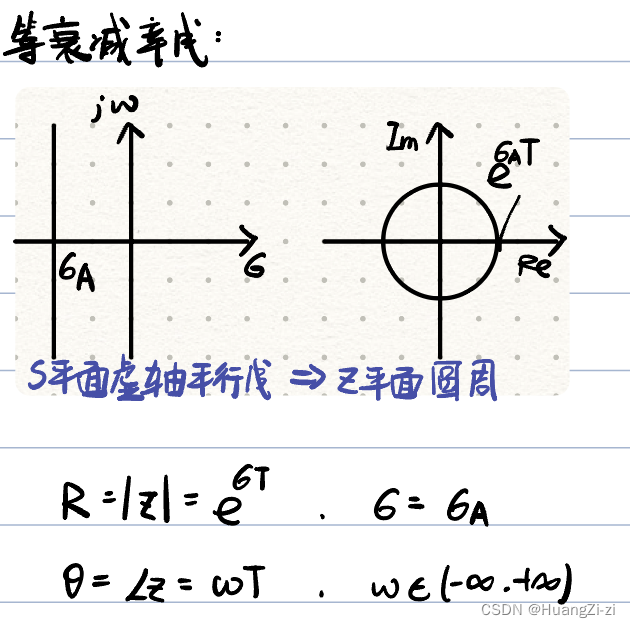
-
等阻尼比轨迹
cosβ=ξ\\cos \\beta=\\xicosβ=ξ,等阻尼比即是S平面过原点的射线
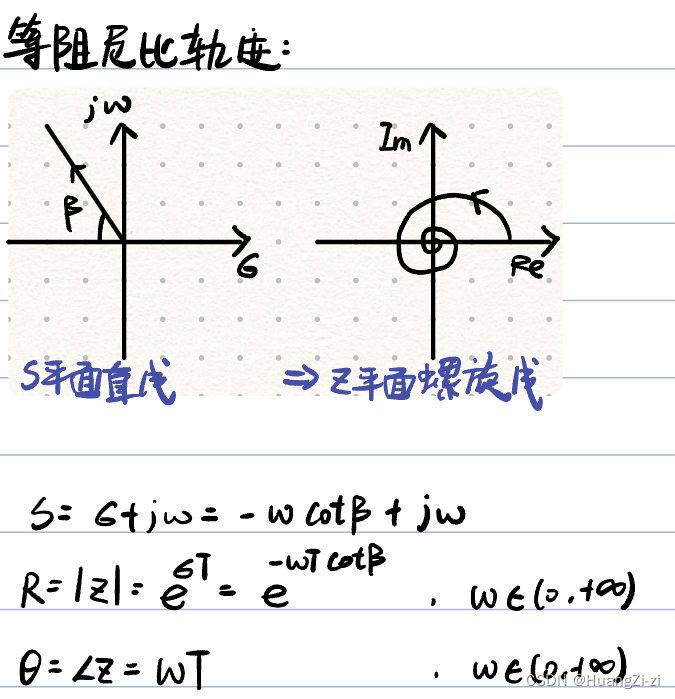
稳定性分析
连续系统稳定:闭环特征根都在S平面的左半平面
根据映射关系:
离散系统稳定:闭环特征根都在Z平面单位圆内
利用特征根判别系统稳定性:
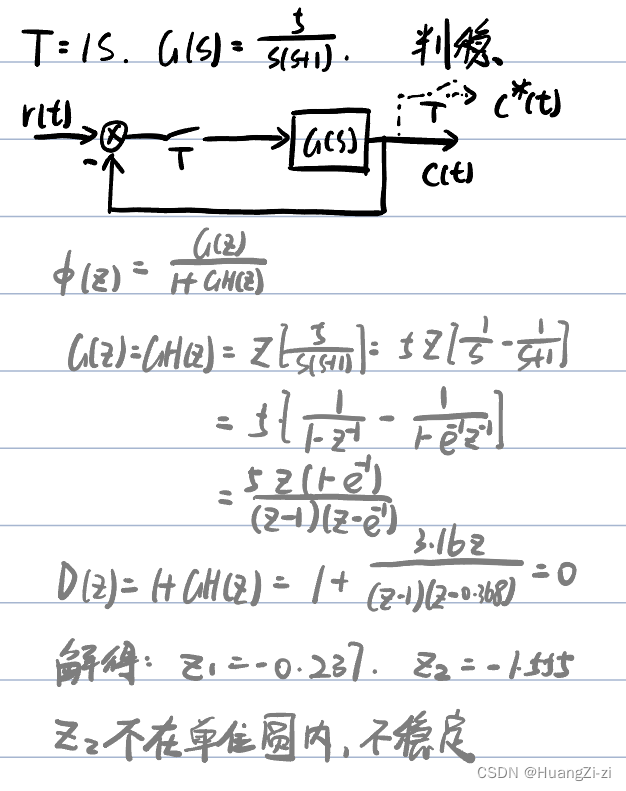
离散Routh判据
Routh判据是用来判断极点是否位于复平面左半平面的。因此需要引入一个新的变换,将Z平面的单位圆内,映射到某个平面的左半平面:
W变换:z=1+w1−w\\displaystyle z=\\frac{1+w}{1-w}z=1−w1+w
运用W变换以后,就可以像之前连续系统一样运用Routh判据了。
两种特殊情况的处理方法:
-
某行第一列为0:
用足够小的正数ε\\varepsilonε替代0参与运算
用因子(w+a)(w+a)(w+a)乘以原特征方程,其中aaa为任意正数 -
某行全为0:
用全0行的上一行构造辅助方程,求导后用其系数替代全0行
看一个综合性的例题:
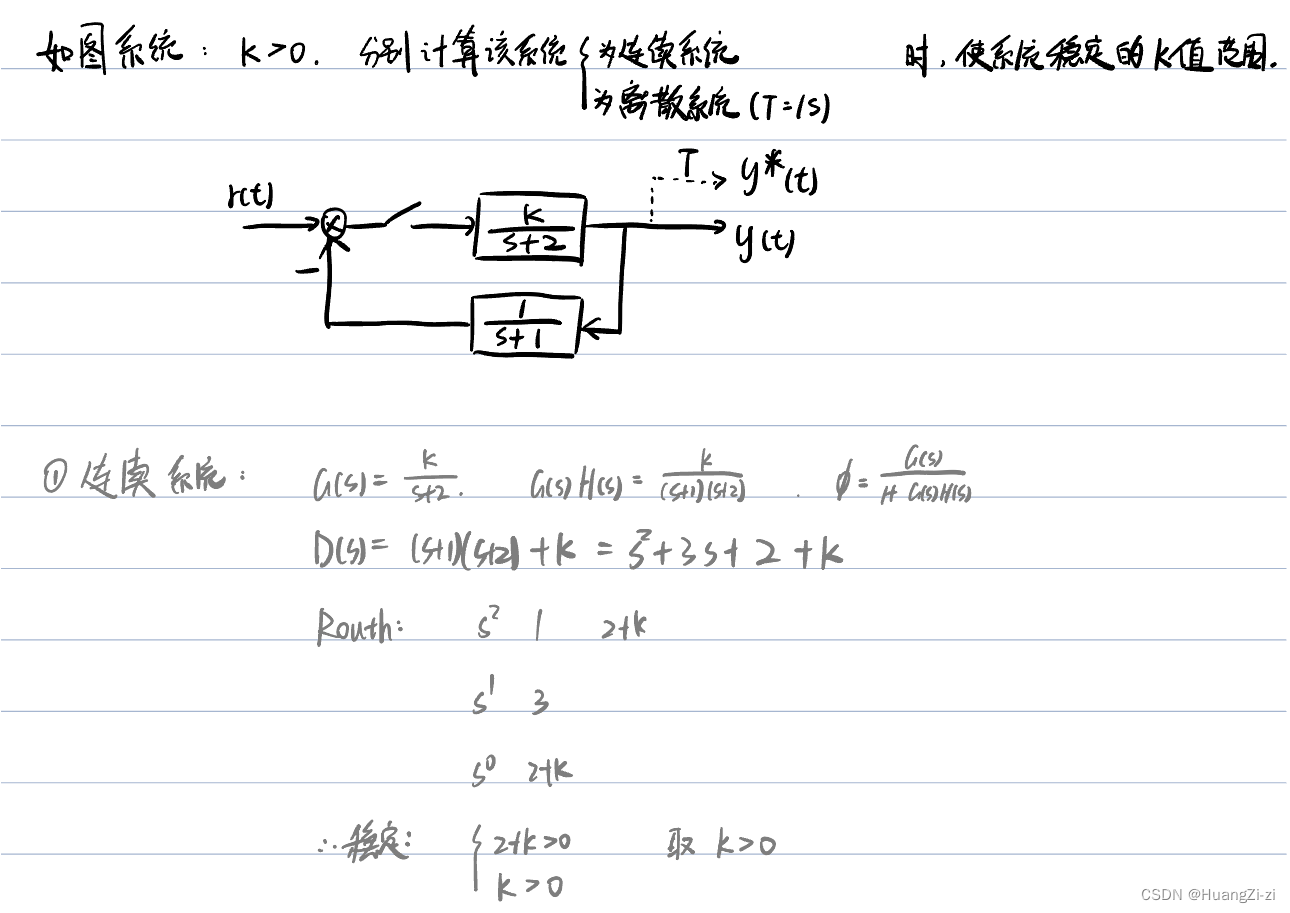

可以看出,采样使得系统的稳定区间变小,不稳定性增加。
但采样周期减小,系统更加接近连续,则这种影响也就减小。
对于特征方程二次的系统,D(z)=z2+Az+B=0D(z)=z^2+Az+B=0D(z)=z2+Az+B=0,
如果满足:
∣D(0)∣=∣B∣<1D(1)=1+A+B>0D(−1)=1−A+B>0\\begin{aligned} &|D(0)|=|B|<1\\\\ &D(1)=1+A+B>0\\\\ &D(-1)=1-A+B>0 \\end{aligned}∣D(0)∣=∣B∣<1D(1)=1+A+B>0D(−1)=1−A+B>0
则系统稳定。
Jury判据
相比与劳斯判据,不需要进行W变换。但缺点是只能判断是否稳定,而无法给出不稳定极点的个数。
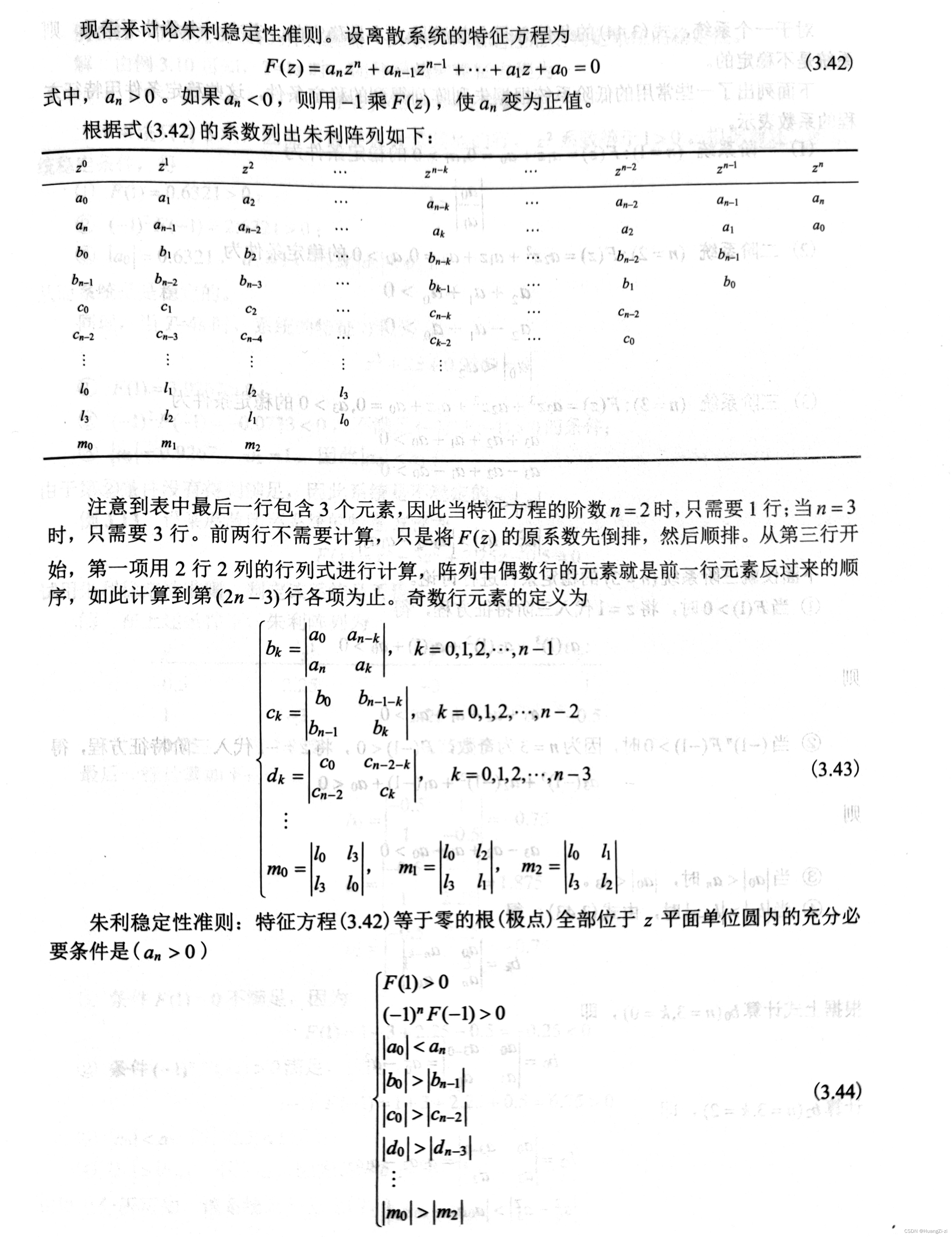
「图源:刘建昌_计算机控制系统」
离散Nyquist判据
(了解)
特征方程:1+kD(z)G(z)=01+kD(z)G(z)=01+kD(z)G(z)=0
- 确定kD(z)G(z)kD(z)G(z)kD(z)G(z)的不稳定极点数p
- 代入z=ejωTz=e^{j \\omega T}z=ejωT,在0≤ωT≤2π0 \\le \\omega T \\le2\\pi0≤ωT≤2π范围内,画出开环幅相频率特性曲线
- 计算曲线顺时针包围z=−1z=-1z=−1的圈数nnn
- q=p−nq=p-nq=p−n,若q=0q=0q=0,则稳定
稳态误差
离散系统的稳态误差和连续系统的非常相近,可以对照进行理解
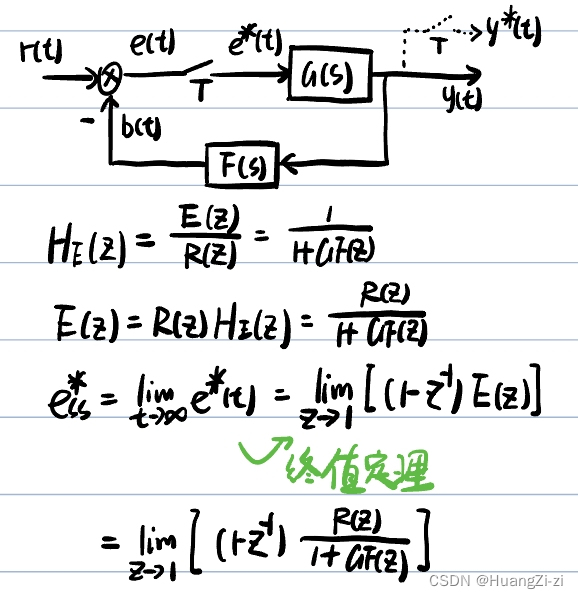
由此可以看出,稳态误差与以下因素都有关:
- 系统本身的结构参数
- 输入的形式和幅值
- 采样周期T
通过定义和终值定理求稳态误差:

静态误差系数
型别的划分:
系统开环传递函数分母包含(z−1)(z-1)(z−1)的阶数称为型别(z=1z=1z=1的极点数)
因此开环传递函数可以写成:
1(z−1)vA(z)B(z)\\displaystyle \\frac{1}{(z-1)^v}\\frac{A(z)}{B(z)}(z−1)v1B(z)A(z),其中v为系统型别
稳态误差:
| 型别v | essp | essv | essa |
|---|---|---|---|
| 0 | A1+Kp\\frac{A}{1+K_p}1+KpA | ∞\\infty∞ | ∞\\infty∞ |
| 1 | 0 | AKv\\frac{A}{K_v}KvA | ∞\\infty∞ |
| 2 | 0 | 0 | AKa\\frac{A}{K_a}KaA |
需要注意的是,静态误差系数的计算不能直接读取增益了,而要根据Z变换的结果来求:
Kp=limz→1GF(z)Kv=limz→1(1−z−1)GF(z)TKa=limz→1(1−z−1)2GF(z)T2\\begin{aligned} &K_p=\\lim_{z\\to 1}GF(z)\\\\ &K_v=\\lim_{z\\to 1} \\frac{(1-z^{-1})GF(z)}{T}\\\\ &K_a=\\lim_{z\\to 1} \\frac{(1-z^{-1})^2GF(z)}{T^2} \\end{aligned}Kp=z→1limGF(z)Kv=z→1limT(1−z−1)GF(z)Ka=z→1limT2(1−z−1)2GF(z)
解释:
- 只有系统稳定才能求稳态误差(计算之前先判稳)
- 稳态误差为∞\\infty∞,并不表示系统不稳定。而是表示系统无法跟踪输入

动态过程
动态特性主要考虑单位阶跃响应。
和连续情况相似,时域的动态性能指标也包括超调量、上升时间、峰值时间、调节时间等等。
但是各个指标的取值是从系统阶跃响应的采样中得到的,因此根据采样的不同,各个值也会不同。
和连续情况类似,时间响应由闭环极点在Z平面的位置决定。
闭环极点与单位脉冲响应:
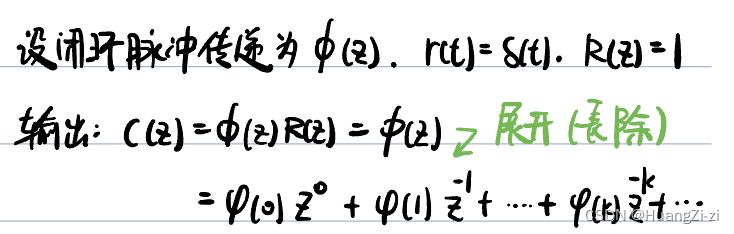
其中φ(k)=∑i=0nRes[ϕ(z)zk−1]z=zi\\displaystyle \\varphi(k)=\\sum_{i=0}^n \\text{Res}[\\rm \\phi(z)z^{k-1}]_{z=z_i}φ(k)=i=0∑nRes[ϕ(z)zk−1]z=zi
因此求出φ(k)\\varphi(k)φ(k),再用Z反变换,就可以求出时间响应。
-
脉冲传函只有一个简单的实极点
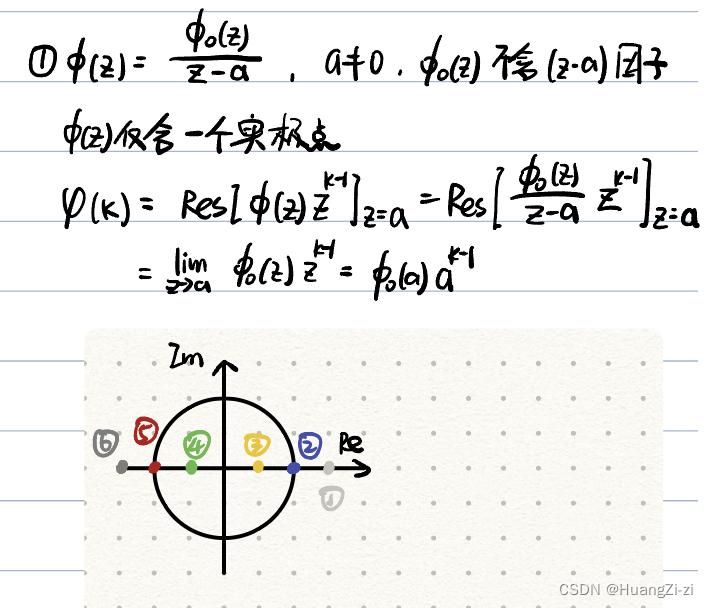
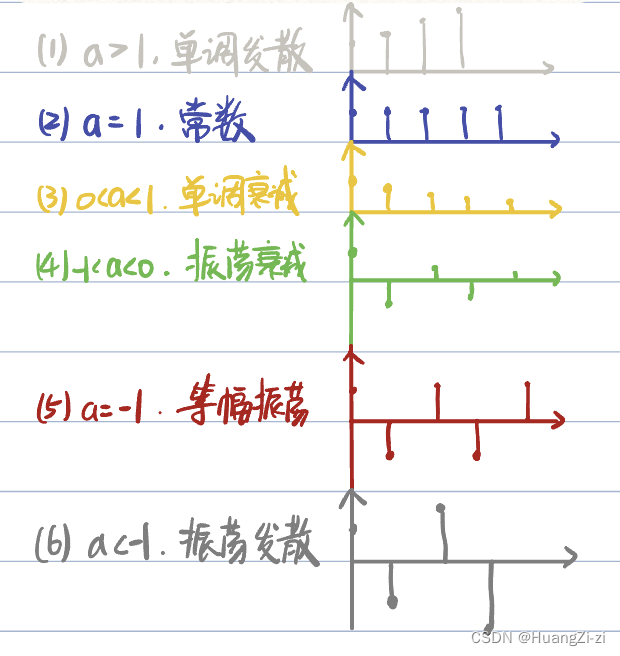
极点越靠近0,衰减越快 -
脉冲传函仅含一对共轭复极点

ρ1=∣a∣\\rho_1=|a|ρ1=∣a∣,两个极点越靠近原点,ρ1\\rho_1ρ1越小,衰减越快,过渡过程影响越小。
θ\\thetaθ增大,震荡频率增大。θ=180°\\theta=180 \\degreeθ=180°震荡频率最高。 -
脉冲传函所有极点都在Z平面原点

φ(k)\\varphi(k)φ(k)只有有限项,也即在单位脉冲作用下,响应在nTnTnT内结束。
当采样频率一定,该系统具有最短的过渡过程,称为时间最优系统或者最小拍系统
所有极点都在原点,稳定性最高。但该条件苛刻,且系统参数变化会使控制性能变差。
频率特性
(了解)
连续系统频率特性:沿虚轴看,s=jωs=j\\omegas=jω
离散系统频率特性:沿单位圆看,z=ejωTz=e^{j\\omega T}z=ejωT
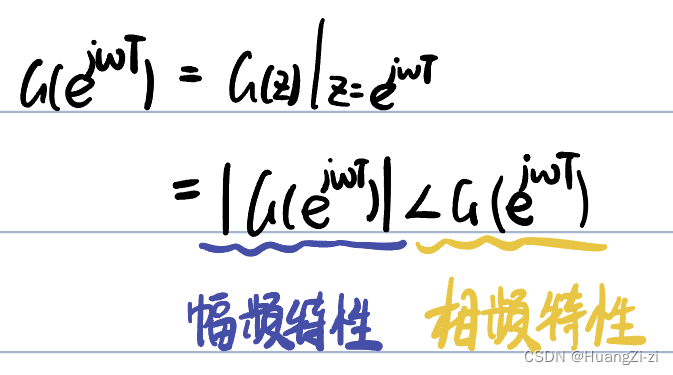
- ωT\\omega TωT沿单位圆转一圈,频率特性重复一次
- ∣G(ejωT)∣|G(e^{j\\omega T})|∣G(ejωT)∣是ω\\omegaω的偶函数,且沿ωs2\\frac{\\omega_s}{2}2ωs对称
- ∠G(ejωT)\\angle G(e^{j \\omega T})∠G(ejωT)是ω\\omegaω的奇函数
- G(ejωT)G(e^{j\\omega T})G(ejωT)不是ω\\omegaω的有理分式函数,不能画出对数幅频特性。但频率轴仍可以用对数座标。
- 离散环节频率特性形状与连续环节相差较大。尤其是T较大时


