C++数据结构:二叉搜索树的结构、模拟实现及应用

目录
一. 二叉搜索树的结构
二. 二叉搜索树的模拟实现
2.1 二叉搜索树的节点及类的成员变量
2.2 数据插入操作Insert的实现
2.3 数据删除操作Erase的实现
2.4 数据查找操作Find的实现
2.5 中序遍历InOrder的实现
2.6 构造函数的实现
2.7 析构函数的实现
三. 二叉搜索树的应用
3.1 二叉搜索树的key模型
3.2 二叉搜索树的key-value模型
四. 二叉搜索树的性能分析
附录一:二叉搜索树的Key模型完整版代码
附录二:二叉搜索树的key-value模型完整版代码
一. 二叉搜索树的结构
二叉搜索树是一种特殊的二叉树,它要么为空树,要么具有一下的结构特点:
- 若根节点的左子节点不为空,那么其左子树节点的值均小于根节点。
- 若根节点的右子节点不为空,那么其右子树节点的值均大于根节点。
- 左子树和右子树也为二叉搜索树(满足1、2条件)。
- 一般要求二叉搜索树中没有重复节点。
在理想情况下,二叉搜索树可以实现时间复杂度为O(logN)的查找操作。

二. 二叉搜索树的模拟实现
2.1 二叉搜索树的节点及类的成员变量
以struct类的形式来定义二叉搜索树的节点,每个节点包含3个成员,分别为:
- _left:本节点的左子节点。
- _right:本节点的右子节点。
- _key:本节点的值。
将class BSTree定义为二叉搜索树模板板类,将模板参数定义为K -- template<class K>,表示节点数据的类型。在其中将节点类型重定义为Node,其中包含成员变量_root,表示根节点指针。同时,在类中声明定义以下成员函数:
- bool Insert(const K& x) / bool InsertR(const K& x) -- 采用非递归和递归的方法插入数据x,插入成功返回true,插入失败返回false。
- bool Erase(const K& x) / bool EraseR(const K& x) -- 采用非递归和递归的方法删除数据x,删除成功返回true,插入失败返回false。
- Node* Find(const K& key) / Node* FindR(const K& key) -- 采用递归和非递归的方法查找存储数据key的节点,找到了返回节点地址,找不到返回nullptr。
- void InOrder() -- 中序遍历函数,根据搜索二叉树的结构特点,采用中序遍历会获得一组升序数据,因此二叉搜索树也叫排序二叉树。
- 默认构造函数、拷贝构造函数和析构函数。
注:带有前缀 _ 的private属性函数,为被相应成员函数调用的子函数,本文将BSTree模板类声明定义在命名空间zhang中。
代码2.1:(节点和BSTree模板类的声明)
template<class K>struct BSTreeNode //二叉搜索树节点{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key): _left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree() = default; //强制编译器生成默认构造函数BSTree(const BSTree<K>& bt); //拷贝构造函数~BSTree(); //析构函数bool Insert(const K& x); //数据插入函数Node* Find(const K& key); //二叉搜索树节点查找函数void InOrder(); //中序遍历函数bool Erase(const K& x); //节点删除函数bool InsertR(const K& x); //递归插入函数bool EraseR(const K& x); //递归删除数据函数Node* FindR(const K& key); //递归查找函数private:Node* _Copy(Node* root); void _Destroy(Node*& root);void _InOrder(Node* root);bool _InsertR(Node*& root, const K& x);bool _EraseR(Node*& root, const K& x);Node* _FindR(Node* root, const K& key);private:Node* _root = nullptr;};2.2 数据插入操作Insert的实现
Insert的非递归实现方法:
- 如果树为空,直接插入节点(将根节点_root变为新增节点)。
- 如果树不为空,这逐层查找要链接新节点的父亲节点parent。如果本节点值小于插入值x,则去右子树查找,若大于插入值x,则去左子树查找,直至找到nullptr为止。
- 如果在查找过程中遇到了值等于x的节点,那么插入失败,函数返回false。
Insert的递归实现方法:
- InsertR的第一个参数为Node*&,采用引用传参,使函数内部可以控制外部参数。
- 查找插入数据的位置,如果本节点值小于插入值x,则去右子树查找,若大于插入值x,则去左子树查找,如果遇到nullptr,那么直接将本层递归的root改为新增节点即可。
- 如果在查找过程中遇到了值等于x的节点,那么插入失败,函数返回false。

代码2.2:(数据插入的非递归实现和递归实现函数)
//搜索二叉树节点非递归插入函数
template<class K>
bool zhang::BSTree<K>::Insert(const K& x)
{if (_root == nullptr){//处理根节点为空(树中没有节点的情况)_root = new Node(x);return false;}Node* cur = _root;Node* parent = nullptr; //插入节点的父亲节点while (cur){parent = cur;if (cur->_key > x){//节点值大于插入数据向左移cur = cur->_left;}else if (cur->_key < x){//节点值小于插入数据向右移cur = cur->_right;}else{//二叉搜索树不允许有重复的节点,如果出现插入节点值和某一节点相同,则插入失败return false;}}cur = new Node(x);if (parent->_key < x){parent->_right = cur;}else{parent->_left = cur;}return true;
}//递归插入函数
template<class K>
bool zhang::BSTree<K>::InsertR(const K& x)
{return _InsertR(_root, x);
}template<class K>
bool zhang::BSTree<K>::_InsertR(Node*& root, const K& x)
{if (root == nullptr){root = new Node(x);}if (root->_key > x){return _InsertR(root->_left, x);}else if(root->_key < x){return _InsertR(root->_right, x);}else{return false;}
}2.3 数据删除操作Erase的实现
删除某个特定的数据的具体方法,应当分为以下三种情况来讨论:
- 若删除的节点为叶子节点,那么直接将其Delete,然后让其父亲节点的指针指向nullptr即可。
- 若删除的节点只有一个子节点,那么判断被删除的节点是否为根节点,如果不是,将这个子节点托管给被删除节点的父亲节点,即让父亲节点的左指针或右指针指向被删节点的子节点,如果是,那么直接将根节点更新为被删节点的子节点。
- 如果删除的节点既有左子节点也有右子节点,那么交换本节点的值与左子树中最大的值或右子树中最小的值,然后删除左子树或右子树中进行了交换的节点即可。
在编写代码是,可将第1、第2种情况合为一体编码。
对于Erase操作的递归实现,如果递归到要删除的节点,判断要删除的节点是否有两个节点,如果没有,只需要将被删节点的子节点直接赋值给本层root即可,如果有,那么执行与非递归实现中相同的节点值互换操作,再递归删除子树中被换的节点即可。

代码2.3:(删除节点的非递归实现和递归实现)
//节点删除函数
template<class K>
bool zhang::BSTree<K>::Erase(const K& x)
{Node* parent = nullptr; //被删除节点的父亲节点Node* cur = _root;while (cur){if (cur->_key < x){parent = cur;cur = cur->_right;}else if (cur->_key > x){parent = cur;cur = cur->_left;}else{//找到要删除的节点,开始删除if (cur->_left == nullptr){if (parent == nullptr) //要删除的节点为根节点{_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;cur = nullptr;}else if(cur->_right == nullptr){if (parent == nullptr) //要删除的节点为根节点{_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;cur = nullptr;}else{//要删除节点的左子节点和右子节点均不为nullptr//交换删除节点与右子树最左侧节点的值Node* leftInRight = cur->_right;Node* parentInRight = cur;//找右子树的最左节点while (leftInRight->_left != nullptr){parentInRight = leftInRight;leftInRight = leftInRight->_left;}std::swap(leftInRight->_key, cur->_key);if (parentInRight == cur){parentInRight->_right = leftInRight->_right;}else{parentInRight->_left = leftInRight->_right;}delete leftInRight;leftInRight = nullptr;return true;}}}return false;
}//递归删除数据函数
template<class K>
bool zhang::BSTree<K>::EraseR(const K& x)
{return _EraseR(_root, x);
}template<class K>
bool zhang::BSTree<K>::_EraseR(Node*& root, const K& x)
{if (root == nullptr){return false;}if (root->_key > x){return _EraseR(root->_left, x);}else if (root->_key < x){return _EraseR(root->_right, x);}else{//删除数据Node* del = root; //带删除的节点if (root->_left == nullptr){root = del->_right;}else if (root->_right == nullptr){root = del->_left;}else{//要删除的节点左右子节点都不为空//去找右子树最小的节点,交换删除Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}std::swap(root->_key, minRight->_key);return _EraseR(root->_right, x);}delete del;del = nullptr;return true;}
}2.4 数据查找操作Find的实现
将节点数据val与要查找的数据key进行比较,如果val小于key,那么到这个节点的右子树去查找,如果val大于key,那么去这个节点的左子树去查找,如果两者相等,那么返回该节点的指针。如果遇到了nullptr,那么表明二叉搜索树中没有key,返回nullptr。
代码2.4:(查找的非递归实现和递归实现)
//递归查找函数
template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::FindR(const K& key)
{return _FindR(_root, key);
}template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::_FindR(Node* root, const K& key)
{if (nullptr == root){return nullptr;}if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return root;}
}//搜索二叉树节点查找函数非递归实现
template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key == key){return cur; //找到节点}else if (cur->_key < key){//向右子树查找cur = cur->_right;}else{//向左子树查找cur = cur->_left;}}return nullptr;
}
2.5 中序遍历InOrder的实现
由于二叉搜索树的左子树的节点均小于根节点,右子树的节点均大于根节点,因此,搜索二叉树中序遍历可以获取一组无重复的升序序列。其实现方法与普通二叉树的中序遍历一致。
代码2.5:(二叉搜索树中序遍历)
//搜索二叉树中序遍历函数(升序)
template<class K>
void zhang::BSTree<K>::InOrder()
{_InOrder(_root);std::cout << std::endl;
}template<class K>
void zhang::BSTree<K>::_InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);std::cout << root->_key << " ";_InOrder(root->_right);
}2.6 构造函数的实现
- 对于默认构造函数,不需要动态开辟内存空间,只需要将_root的值置为nullptr即可,我们可以在声明成员变量_root时就给定初值nullptr,这样使用编译的生成的默认构造函数即可。
- 对于拷贝构造函数,需要按照前序遍历的方式,依次创建每个节点,并对每个节点进行链接。
注:如果显示定义了拷贝构造函数,那么编译器在一般情况下就不会自动生成默认构造函数。此时,应当使用下面的指令来强制编译器生成默认构造函数:
BSTree() = default; //强制编译器生成默认构造函数
代码2.6:(拷贝构造函数)
//拷贝构造函数
template<class K>
zhang::BSTree<K>::BSTree(const BSTree<K>& bt)
{_root = _Copy(bt._root);
}template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::_Copy(Node* root)
{if (root == nullptr){return nullptr;}Node* newNode = new Node(root->_key);newNode->_left = _Copy(root->_left);newNode->_right = _Copy(root->_right);return newNode;
}2.7 析构函数的实现
按照后序遍历的方式,依次释放每个节点即可。
代码2.7:(析构函数)
//析构函数
template<class K>
zhang::BSTree<K>::~BSTree()
{_Destroy(_root);
}template<class K>
void zhang::BSTree<K>::_Destroy(Node*& root)
{if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;root = nullptr;
}三. 二叉搜索树的应用
3.1 二叉搜索树的key模型
key模型,是查找模型,第二章中所实现的就是搜索二叉树的key模型,其只存储一个key值作为关键码,关键码为用于搜索的值。
- 学生宿舍门禁系统:将所有学生的学号存入一颗二叉搜索树(AVL树、红黑树),当学生刷卡时,读取学生的学号,然后到存有学生信息的二叉搜索树中匹配,如果查找到了该学生,就开门,否则报警。
- 单词拼写检查:将库中所有单词存入一颗二叉搜索树,在其中查找某个单词,如果找不到,就报拼写错误。
3.2 二叉搜索树的key-value模型
每个节点中存储一个关键码key和一个与之对于的value值,即存储<key, value>的键值对,通过查找key值,获取与之对应的value。key-value模型与key模型没有任何本质区别,只是多存储了一个value值而已。
- 中英互译软件:输入英文,到搜索二叉树中查找这个单词,然后输出与之匹配的汉语。
四. 二叉搜索树的性能分析
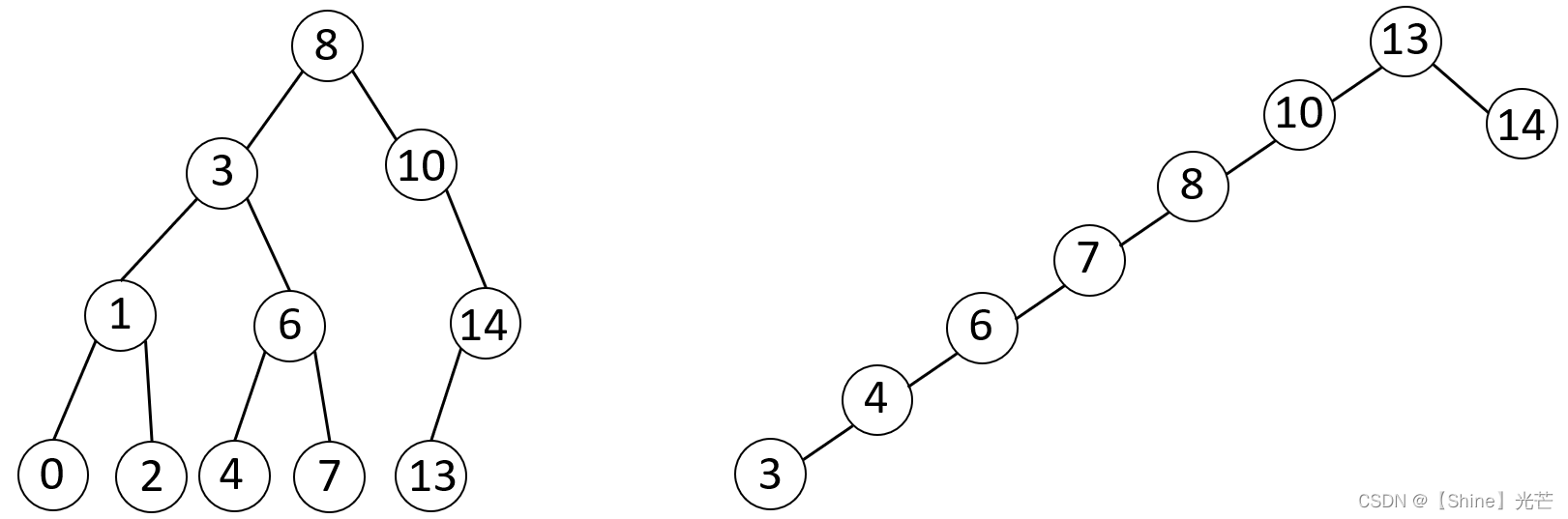
- 在最理想的情况下(除最后一层以外每层节点数量均达到最大值),使用二叉搜索树查找的时间复杂度为O(logN)。
- 在最坏情况下(二叉搜索树的左子树或右子树为空,或某颗子树的节点数远小于另一颗),使用二叉搜索树查找的时间复杂度为O(N)。
由此可见,二叉搜索树的结构对查找效率存在显著影响,这依赖于数据插入的顺序。通过使用AVL树和红黑树,可以避免这一缺陷。
附录一:二叉搜索树的Key模型完整版代码
namespace zhang
{template<class K>struct BSTreeNode //二叉搜索树节点{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key): _left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree() = default; //强制编译器生成默认构造函数BSTree(const BSTree<K>& bt); //拷贝构造函数~BSTree(); //析构函数bool Insert(const K& x); //数据插入函数Node* Find(const K& key); //二叉搜索树节点查找函数void InOrder(); //中序遍历函数bool Erase(const K& x); //节点删除函数bool InsertR(const K& x); //递归插入函数bool EraseR(const K& x); //递归删除数据函数Node* FindR(const K& key); //递归查找函数private:Node* _Copy(Node* root); void _Destroy(Node*& root);void _InOrder(Node* root);bool _InsertR(Node*& root, const K& x);bool _EraseR(Node*& root, const K& x);Node* _FindR(Node* root, const K& key);private:Node* _root = nullptr;};
}//拷贝构造函数
template<class K>
zhang::BSTree<K>::BSTree(const BSTree<K>& bt)
{_root = _Copy(bt._root);
}template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::_Copy(Node* root)
{if (root == nullptr){return nullptr;}Node* newNode = new Node(root->_key);newNode->_left = _Copy(root->_left);newNode->_right = _Copy(root->_right);return newNode;
}//析构函数
template<class K>
zhang::BSTree<K>::~BSTree()
{_Destroy(_root);
}template<class K>
void zhang::BSTree<K>::_Destroy(Node*& root)
{if (root == nullptr){return;}_Destroy(root->_left);_Destroy(root->_right);delete root;root = nullptr;
}//递归查找函数
template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::FindR(const K& key)
{return _FindR(_root, key);
}template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::_FindR(Node* root, const K& key)
{if (nullptr == root){return nullptr;}if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return root;}
}//递归删除数据函数
template<class K>
bool zhang::BSTree<K>::EraseR(const K& x)
{return _EraseR(_root, x);
}template<class K>
bool zhang::BSTree<K>::_EraseR(Node*& root, const K& x)
{if (root == nullptr){return false;}if (root->_key > x){return _EraseR(root->_left, x);}else if (root->_key < x){return _EraseR(root->_right, x);}else{//删除数据Node* del = root; //带删除的节点if (root->_left == nullptr){root = del->_right;}else if (root->_right == nullptr){root = del->_left;}else{//要删除的节点左右子节点都不为空//去找右子树最小的节点,交换删除Node* minRight = root->_right;while (minRight->_left){minRight = minRight->_left;}std::swap(root->_key, minRight->_key);return _EraseR(root->_right, x);}delete del;del = nullptr;return true;}
}//递归插入函数
template<class K>
bool zhang::BSTree<K>::InsertR(const K& x)
{return _InsertR(_root, x);
}template<class K>
bool zhang::BSTree<K>::_InsertR(Node*& root, const K& x)
{if (root == nullptr){root = new Node(x);}if (root->_key > x){return _InsertR(root->_left, x);}else if(root->_key < x){return _InsertR(root->_right, x);}else{return false;}
}//搜索二叉树节点插入函数
template<class K>
bool zhang::BSTree<K>::Insert(const K& x)
{if (_root == nullptr){//处理根节点为空(树中没有节点的情况)_root = new Node(x);return false;}Node* cur = _root;Node* parent = nullptr; //插入节点的父亲节点while (cur){parent = cur;if (cur->_key > x){//节点值大于插入数据向左移cur = cur->_left;}else if (cur->_key < x){//节点值小于插入数据向右移cur = cur->_right;}else{//二叉搜索树不允许有重复的节点,如果出现插入节点值和某一节点相同,则插入失败return false;}}cur = new Node(x);if (parent->_key < x){parent->_right = cur;}else{parent->_left = cur;}return true;
}//搜索二叉树节点查找函数
template<class K>
zhang::BSTreeNode<K>* zhang::BSTree<K>::Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key == key){return cur; //找到节点}else if (cur->_key < key){//向右子树查找cur = cur->_right;}else{//向左子树查找cur = cur->_left;}}return nullptr;
}//搜索二叉树中序遍历函数(升序)
template<class K>
void zhang::BSTree<K>::InOrder()
{_InOrder(_root);std::cout << std::endl;
}template<class K>
void zhang::BSTree<K>::_InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);std::cout << root->_key << " ";_InOrder(root->_right);
}//节点删除函数
template<class K>
bool zhang::BSTree<K>::Erase(const K& x)
{Node* parent = nullptr; //被删除节点的父亲节点Node* cur = _root;while (cur){if (cur->_key < x){parent = cur;cur = cur->_right;}else if (cur->_key > x){parent = cur;cur = cur->_left;}else{//找到要删除的节点,开始删除if (cur->_left == nullptr){if (parent == nullptr) //要删除的节点为根节点{_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;cur = nullptr;}else if(cur->_right == nullptr){if (parent == nullptr) //要删除的节点为根节点{_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;cur = nullptr;}else{//要删除节点的左子节点和右子节点均不为nullptr//交换删除节点与右子树最左侧节点的值Node* leftInRight = cur->_right;Node* parentInRight = cur;//找右子树的最左节点while (leftInRight->_left != nullptr){parentInRight = leftInRight;leftInRight = leftInRight->_left;}std::swap(leftInRight->_key, cur->_key);if (parentInRight == cur){parentInRight->_right = leftInRight->_right;}else{parentInRight->_left = leftInRight->_right;}delete leftInRight;leftInRight = nullptr;return true;}}}return false;
}附录二:二叉搜索树的key-value模型完整版代码
namespace zhang
{template<class K, class V>struct BSTreeNode //二叉搜索树节点{BSTreeNode* _left; //左子节点BSTreeNode* _right; //右子节点K _key; //关键字V _val; //映射值BSTreeNode(const K& key, const V& val): _left(nullptr), _right(nullptr), _key(key), _val(val){ }};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& val); //数据插入函数void InOrder(); //中序遍历函数bool Erase(const K& key); //数据删除函数Node* find(const K& key); //查找函数private:Node* _find(Node* root, const K& key);void _InOrder(Node* root);private:Node* _root = nullptr; //根节点};
}//查找函数
template<class K, class V>
zhang::BSTreeNode<K, V>* zhang::BSTree<K, V>::find(const K& key)
{return _find(_root, key);
}template<class K, class V>
zhang::BSTreeNode<K, V>* zhang::BSTree<K, V>::_find(Node* root, const K& key)
{if (root == nullptr){return nullptr;}if (root->_key > key){return _find(root->_left, key);}else if (root->_key < key){return _find(root->_right, key);}else{//std::cout << key << "->" << root->_val << std::endl;return root;}
}template<class K, class V>
bool zhang::BSTree<K, V>::Erase(const K& key)
{Node* cur = _root;Node* parent = nullptr;while (cur){//查找要删除的节点if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//开始删除数据if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right; //删除了根节点delete cur;}else{//删除非根节点if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}delete cur;}}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left; //删除了根节点delete cur;}else{//删除非根节点if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;}}else{//要删除的节点的左右子节点均不为空//1.找右子树中最小的节点Node* minRight = cur->_right;Node* parentMin = cur;while (minRight->_left){parentMin = minRight;minRight = minRight->_left;}std::swap(cur->_key, minRight->_key);std::swap(cur->_val, minRight->_val);if (parentMin == cur){parentMin->_right = minRight->_right;}else{parentMin->_left = minRight->_right;}delete minRight;}return true;}}return false;
}template<class K, class V>
void zhang::BSTree<K, V>::InOrder()
{_InOrder(_root);std::cout << std::endl;
}template<class K, class V>
void zhang::BSTree<K, V>::_InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);std::cout << "<" << root->_key << "," << root->_val << ">" << " ";_InOrder(root->_right);
}template<class K, class V>
bool zhang::BSTree<K, V>::Insert(const K& key, const V& val)
{if (_root == nullptr) //二叉树为空{_root = new Node(key, val);return true;}//二叉搜索树不为空Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_key > key){//根节点值大于关键字,向左树移动parent = cur;cur = cur->_left;}else if (cur->_key < key){//根节点值小于关键字,向右子树移动parent = cur;cur = cur->_right;}else{//二叉搜索树中不允许有相同节点,遇到相同节点插入失败,返回falsereturn false;}}//判断应该插入到左子树还是右子树if (parent->_key < key){parent->_right = new Node(key, val);}else{parent->_left = new Node(key, val);}return true;
}