归并排序的非递归实现

其实想法和递归实现的类似，只不过是通过其他变量分组，而不是mid，我们可以将数组先分为两

两一组，再合并成四四一组，以此类推，最后一次合并排序后，得到的数组就为有序数组了，所以

递归与非递归的合并的单趟排序是相同的，都是进行找小（或找大）来实现的。

我么应该如何实现分组呢？定义一个变量gap，当 gap = 1 的时候就是两两分组，当 gap = 2的

时候就是四四分组，以此类推，排位有序。

如下图所示：

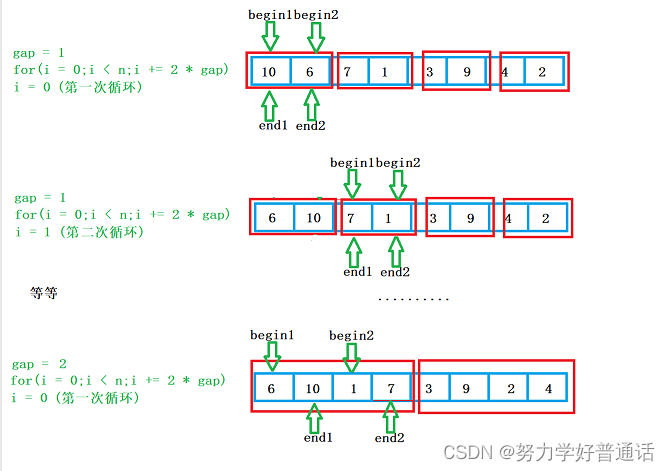
 对应上图的例子，如果 gap = 4 的时候，对应的end1，begin2，end2都可能越界，所以我们应该

在赋值后再进行判断是否越界，如果越界，那就重新赋值，使他们都在数组范围之内，从而不越

界，在这种情况下，就可以全部拷贝，不用分部，在一次内部循环结束后进行一次拷贝， 当然也

可以部分拷贝，大家可以下去自己实现：

具体的赋值与修改代码如下：

            int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;if (end1 >= n){end1 = n - 1;begin2 = n;end2 = n - 1;}if (begin2 >= n){begin2 = n;end2 = n - 1;}if (end2 >= n){end2 = n - 1;}

 赋值以后会直接跳出单趟的合并循环，从而达到不会越界赋值。

整体代码如下：

void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;if (end1 >= n){end1 = n - 1;begin2 = n;end2 = n - 1;}if (begin2 >= n){begin2 = n;end2 = n - 1;}if (end2 >= n){end2 = n - 1;}//归并int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] >= a[begin2]) {tmp[j++] = a[begin2++];}else{tmp[j++] = a[begin1++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}}//全部拷贝(梭哈)memcpy(a, tmp, sizeof(int) * n);gap *= 2;}free(tmp);
}

 切记要释放了动态开辟的内存，这就是合并排序的非递归！