史上最负盛名的平衡二叉树–红黑树，但其实就是2-3树的一种实现

一、红黑树性质

也是BST，每一个节点都有颜色

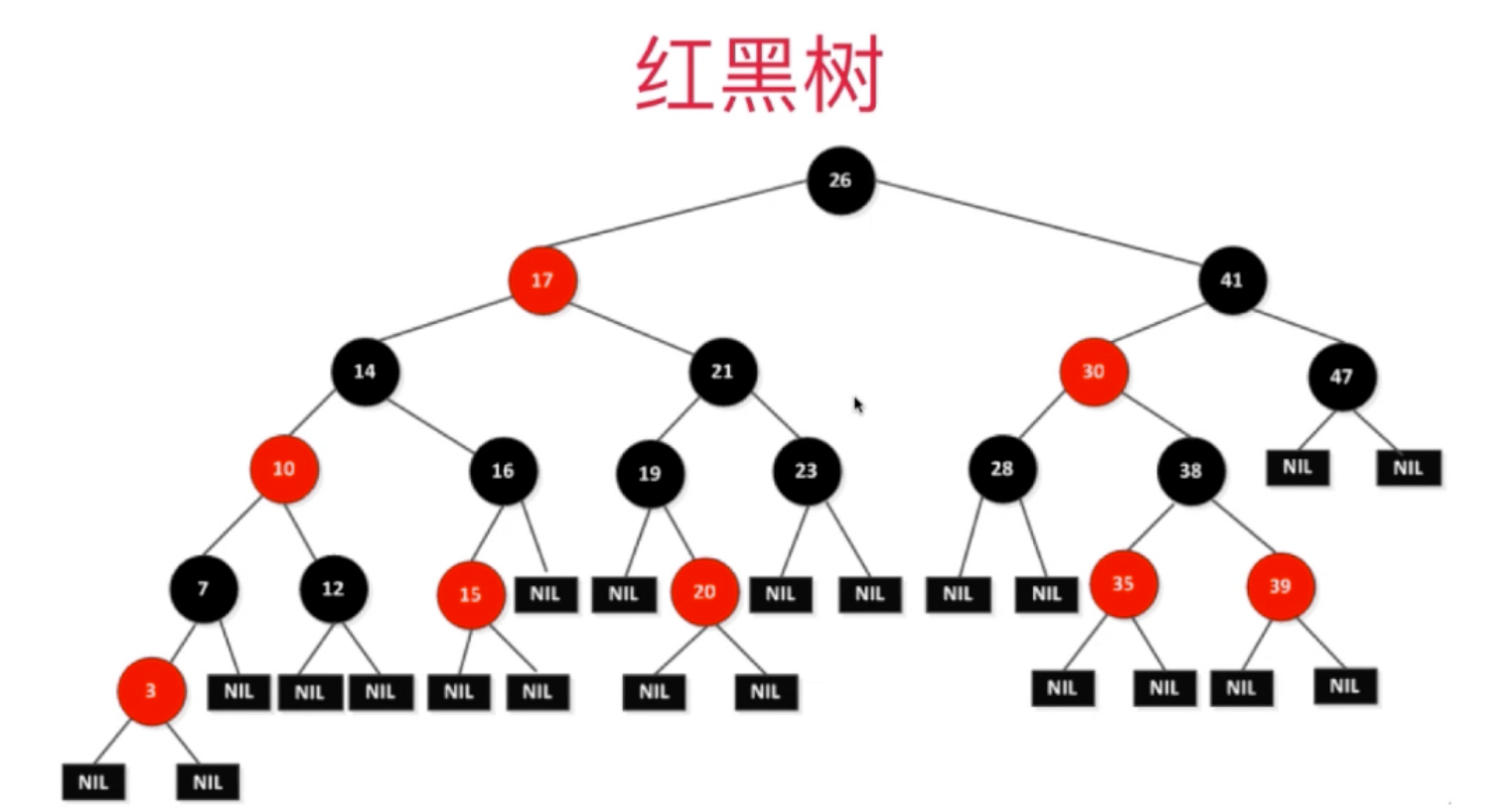
性质 看 后面推导出来的结论

二、红黑树性质推导过程

2-3树

2-3树：和红黑树是等价的
满足BST的基本性质，但不是一种二叉树
有两种节点：

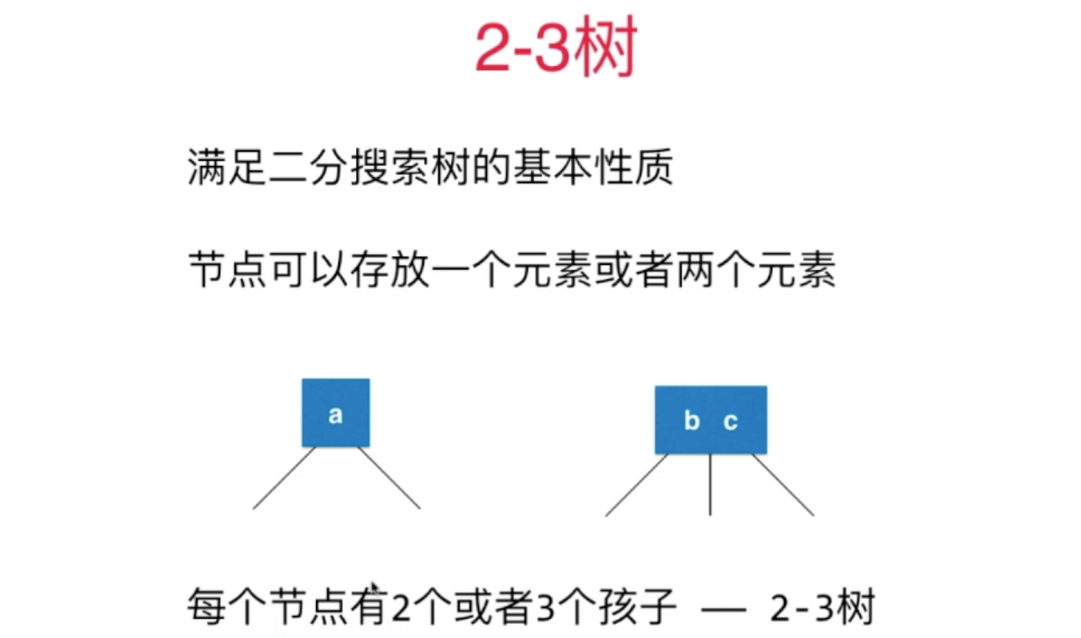
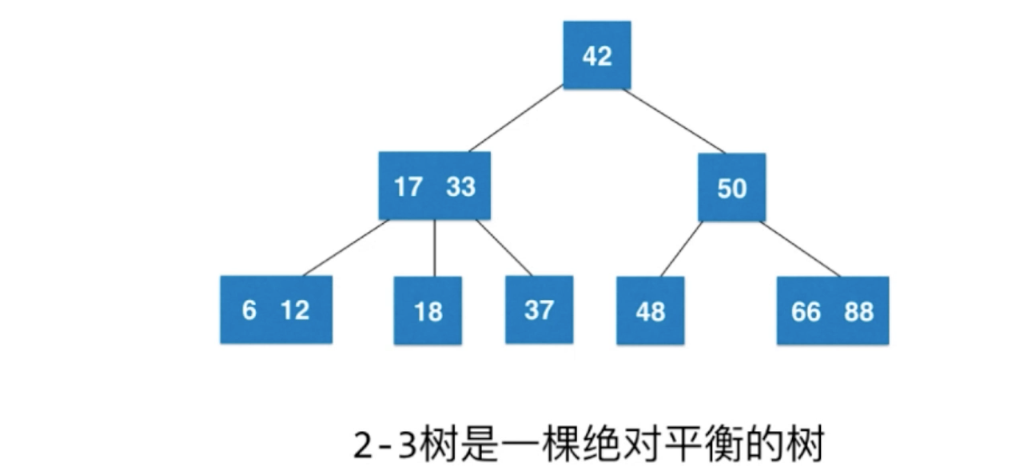
2-3 绝对平衡：根节点到叶子节点 一定相同

2.3.1 如何维护绝对平衡2-3树

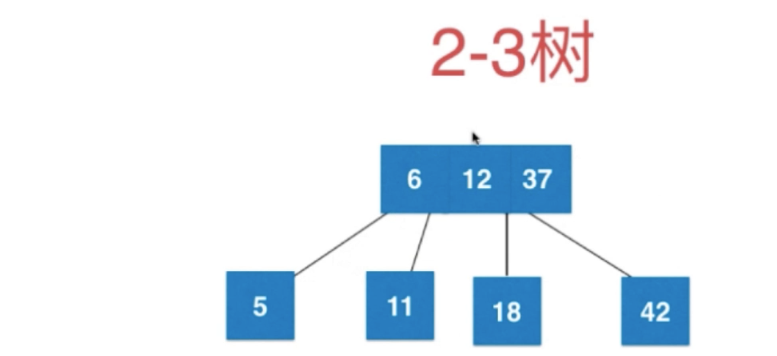
add 2点会变3节点

再添加，3节点会 先融合 形成4节点

再对这个4节点分裂成 BST

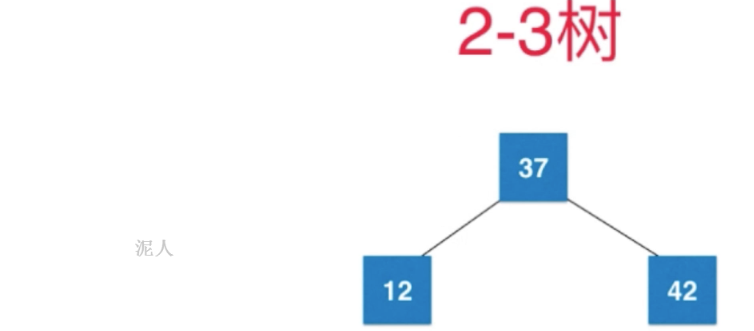
再添加 18 ，会直接在12上形成3节点

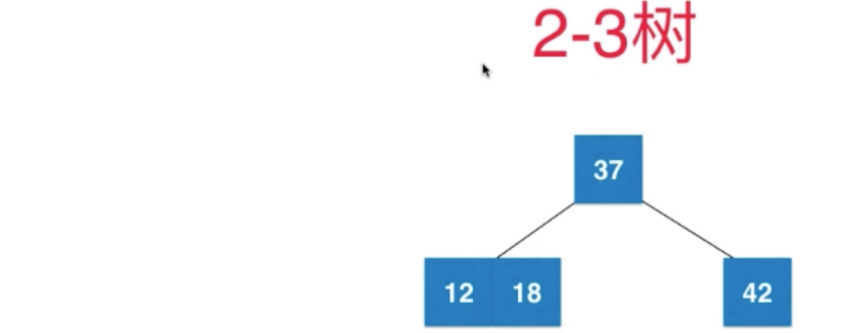
再添加节点6

• 先形成4节点，再拆分
  
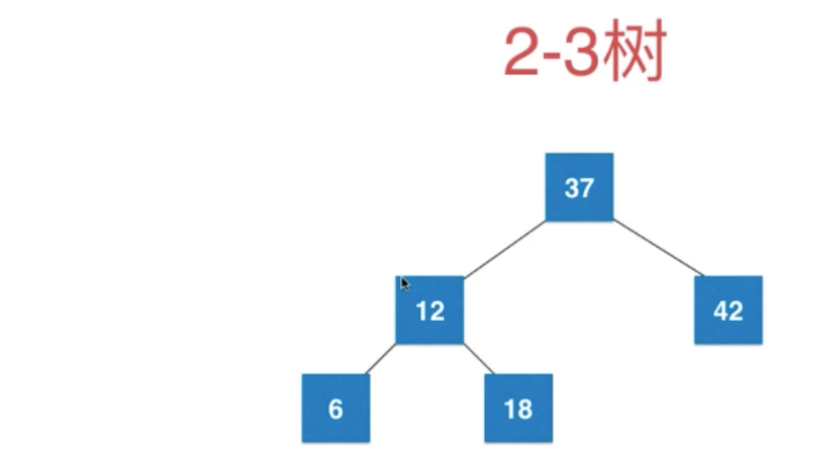
  但是这样就不是决定平衡了
  因此需要向上融合
  
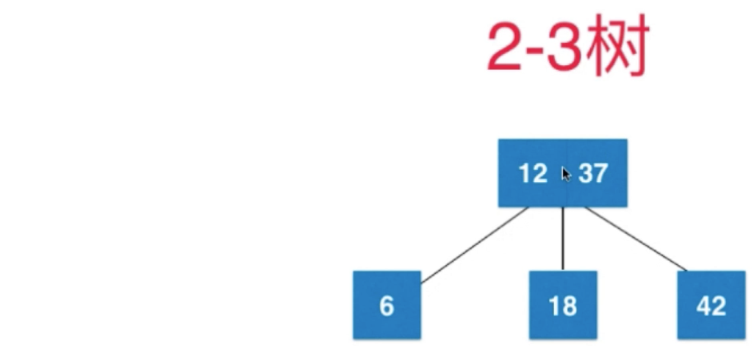
  再添加11, 直接在6上融合成3节点

再添加5，融合在分裂

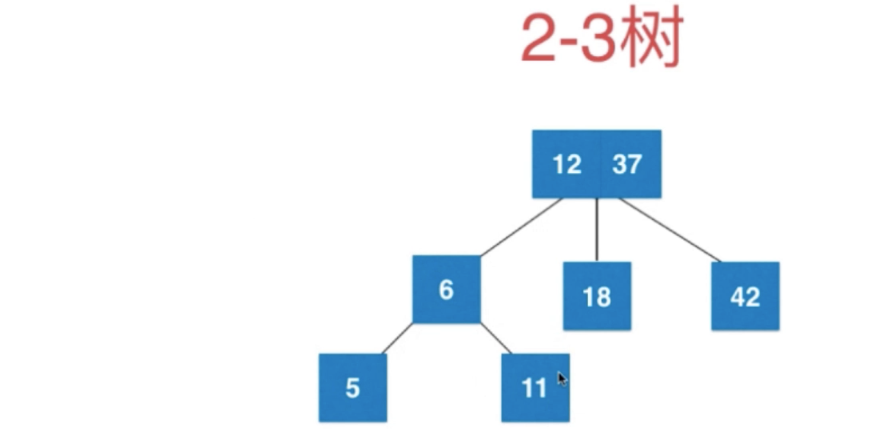
还需要向上融合

这次还需要向下分裂了

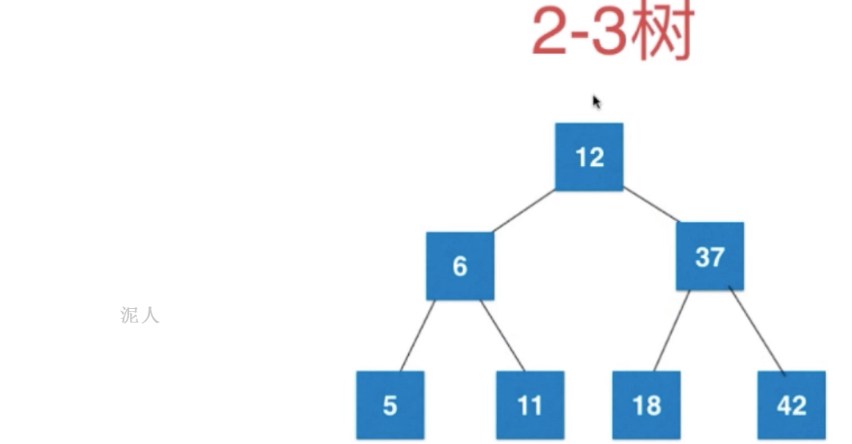
2.3.2 红黑树&2-3树

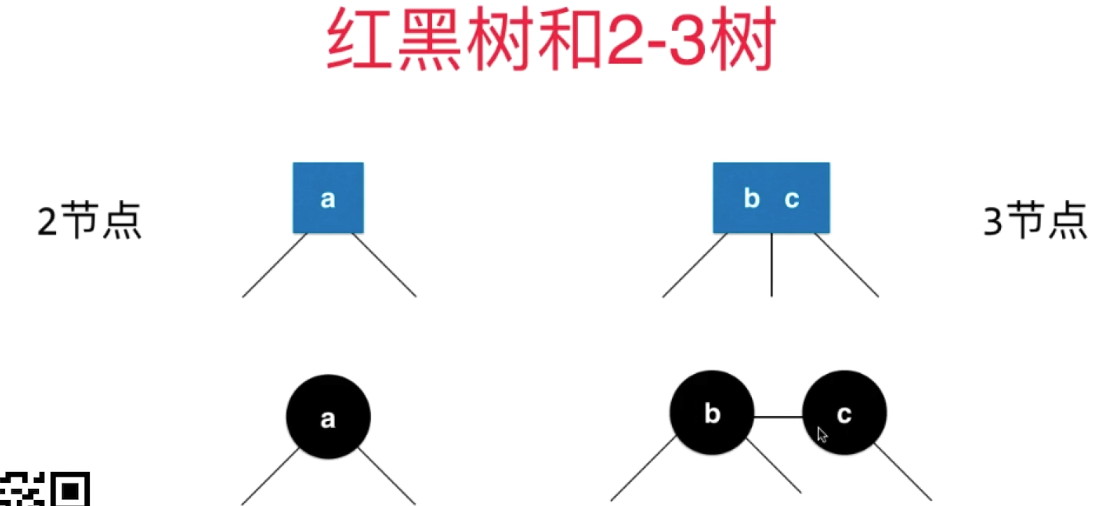
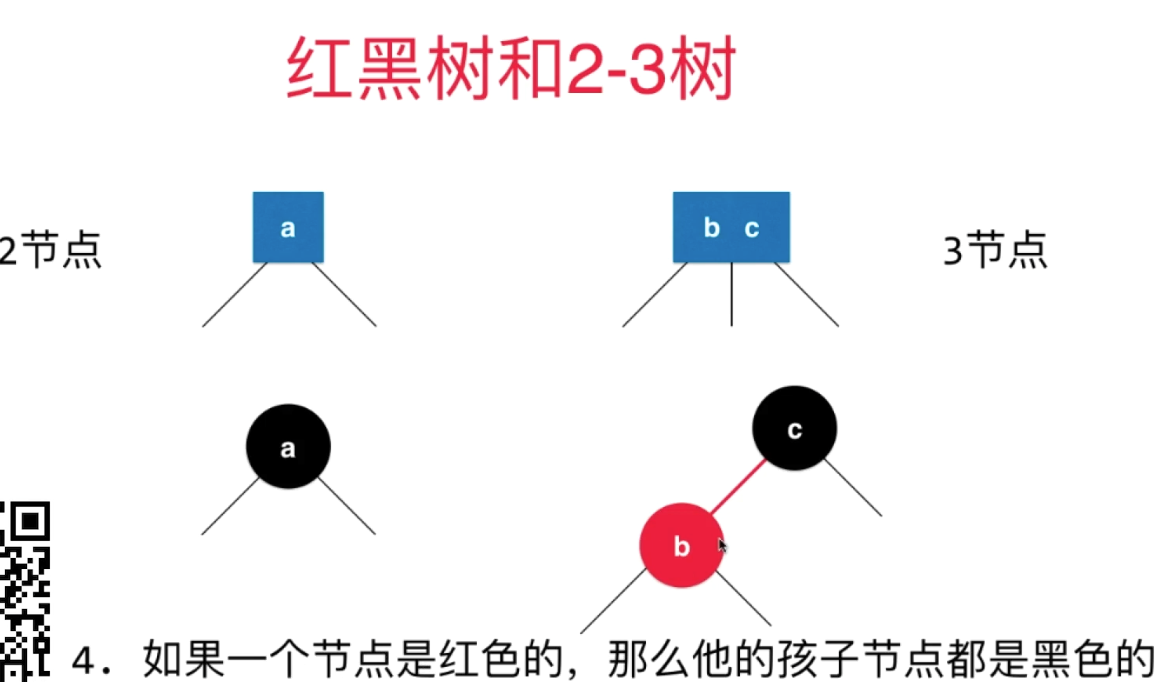
b - c 之间的边用红色表示，代表b & c是在2-3树的同一个节点的

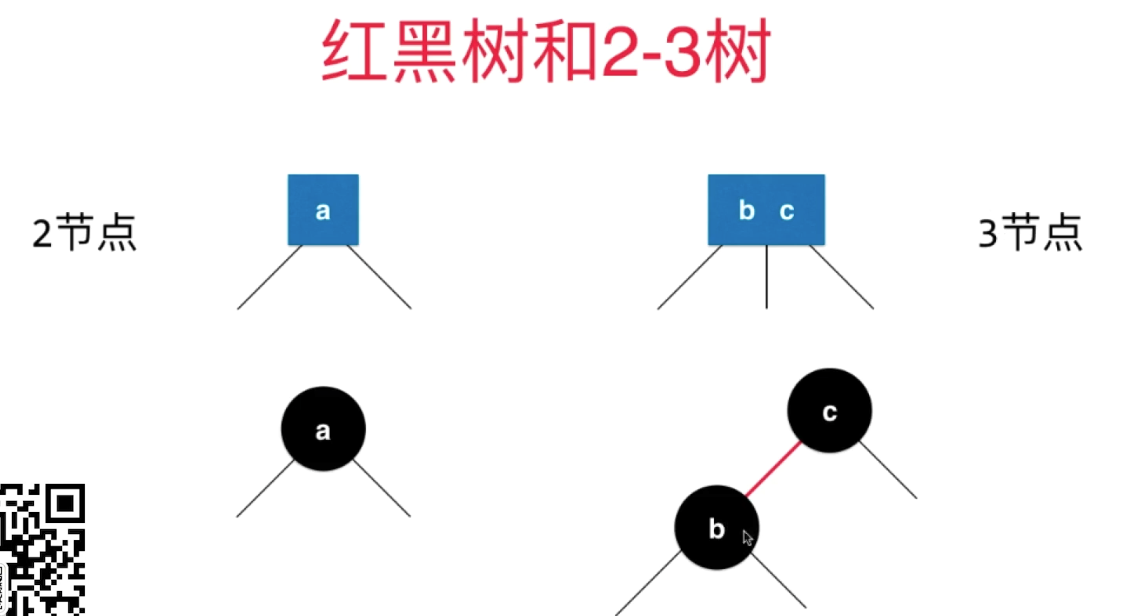
BST中对于边是没有特殊标识的，红色如何标识？
所以就用节点的颜色

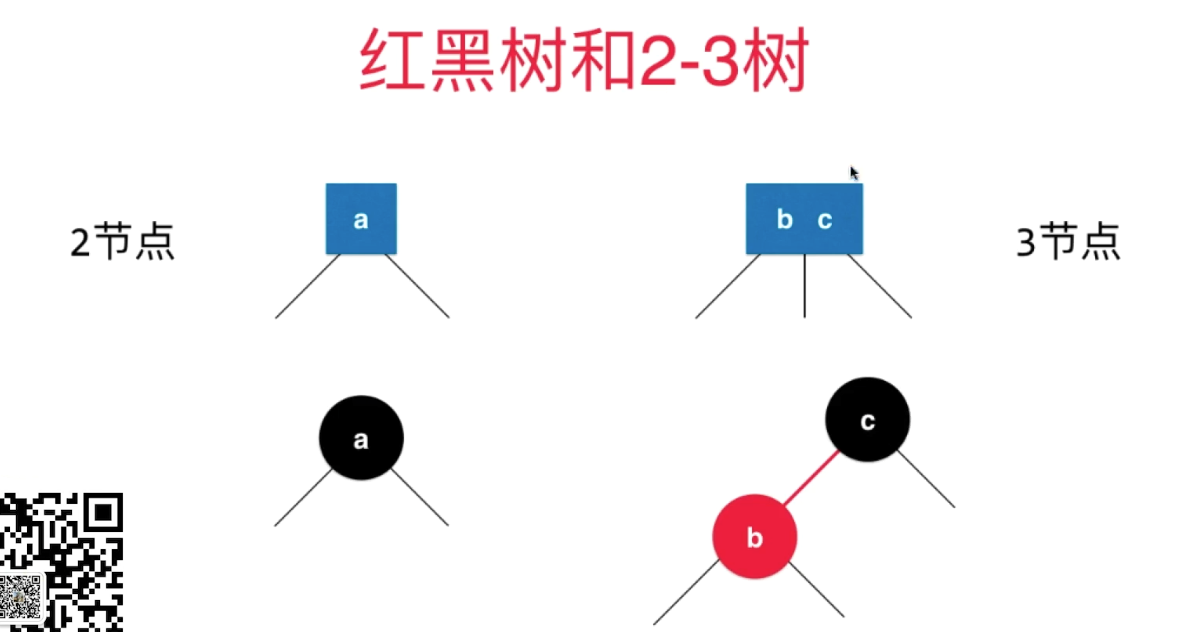
b标记为红色，标识代表 红色的b 和 黑色的c是在同一个节点上的

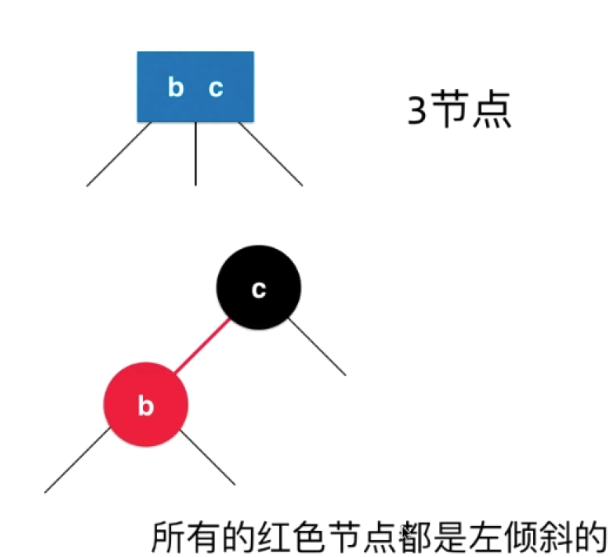
因为把b当做子节点来看待的，是人为定义的

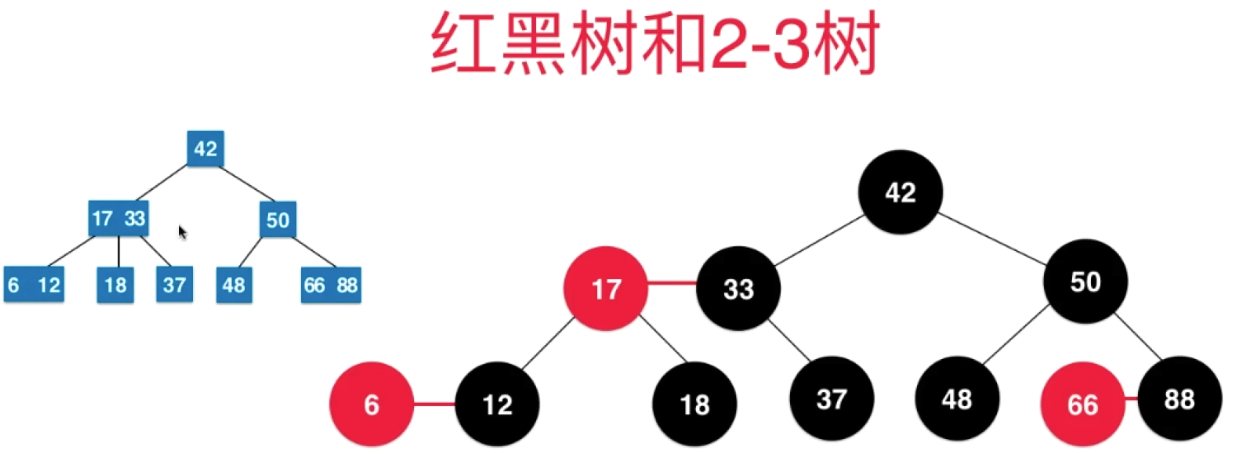
2.3.3 再来看红黑树的性质

1.每个节点为 Black or Red

2.根节点是Black

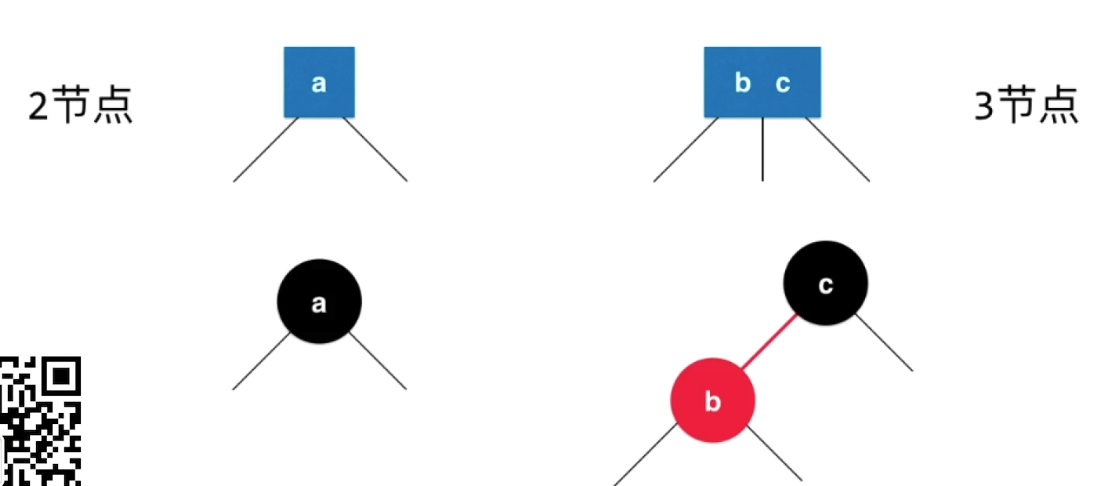
红色的是往下的

3.每一个叶子节点(最后的空节点)是黑色的

其实这不是性质 而是定义，定义空节点是黑色的

4.if 节点 是红色的，so 他的孩子节点都是黑色的

4.2 黑色节点的右孩子一定是黑色的

因为右边也是红色的话，就会分裂了

5.从任意一个节点到叶子节点，经过的黑色节点是一样的

2-3树是绝对平衡的：从2-3数任意节点出发到叶子节点是相同的

在红黑树中就是 经过的黑色的节点，
所以也就说，红黑树是一种保持 黑平衡 的二叉树(不是平衡二叉树)

红黑树 最大高度：2long(n) O(logn)

三、红黑树实现

添加 红黑 标记 ，用Boolean实现就可以

    private static final boolean RED = true;private static final boolean BLACK = false;private class Node{public K key;public V value;public Node left, right;public boolean color;public Node(K key, V value){this.key = key;this.value = value;left = null;right = null;color = RED;}}

判断是否是红节点，主要处理空节点

    // 判断节点node的颜色private boolean isRed(Node node){if(node == null)return BLACK;return node.color;}

3.2 红黑树add

添加到2-节点，形成3-节点
添加到3-节点，暂时形成4-节点，再分裂
新添加的节点首先应该是红节点(2-3中先融合进节点)，后续再调整

保持根节点为黑色的

    // 向红黑树中添加新的元素(key, value)public void add(K key, V value){root = add(root, key, value);root.color = BLACK; // 最终根节点为黑色节点}

3.2.1 左旋

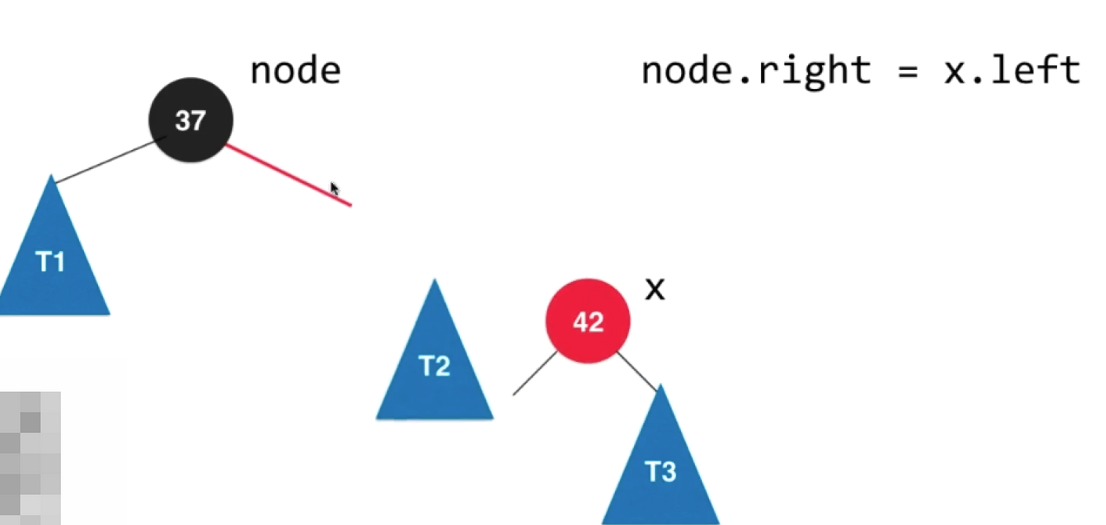
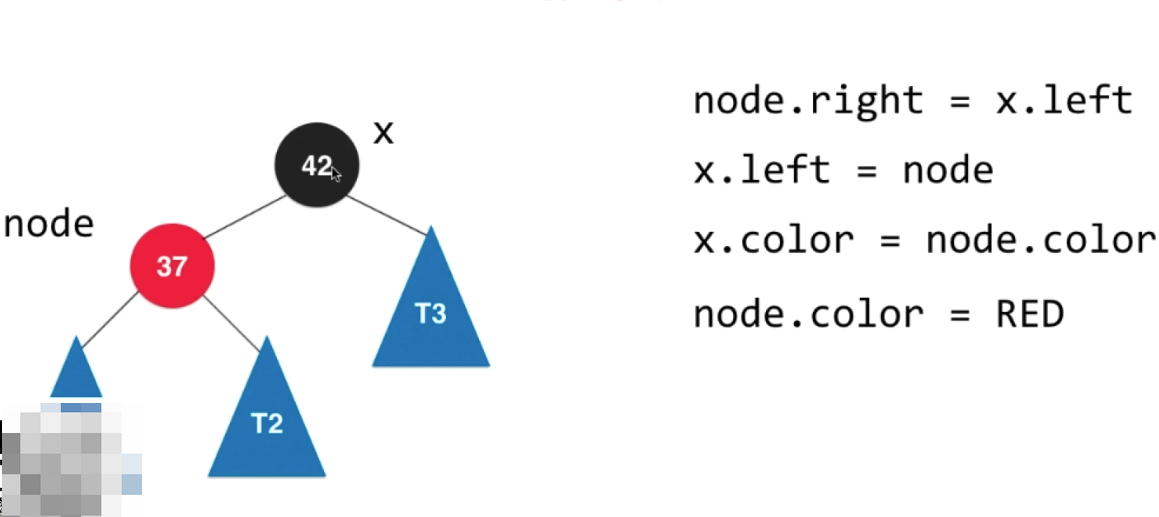
    //   node                     x//  /   \\     左旋转         /  \\// T1   x   --------->   node   T3//     / \\              /   \\//    T2 T3            T1   T2private Node leftRotate(Node node){Node x = node.right;// 左旋转node.right = x.left;x.left = node;x.color = node.color;node.color = RED;return x;}

    // 向以node为根的红黑树中插入元素(key, value)，递归算法// 返回插入新节点后红黑树的根private Node add(Node node, K key, V value){if(node == null){size ++;return new Node(key, value); // 默认插入红色节点}if(key.compareTo(node.key) < 0)node.left = add(node.left, key, value);else if(key.compareTo(node.key) > 0)node.right = add(node.right, key, value);else // key.compareTo(node.key) == 0node.value = value;return node;}

…