【算法】DFS与BFS

作者:指针不指南吗
专栏:算法篇🐾题目的模拟很重要!!🐾
文章目录
- 1.区别
- 2.DFS
-
- 2.1 排列数字
- 2.2 n-皇后问题
- 3.BFS
-
- 3.1走迷宫
1.区别
| 搜索类型 | 数据结构 | 空间 | 用途 | 过程 |
|---|---|---|---|---|
| DFS | stack | O( n ) | 不能用于最短路 | 搜索到最深处,回溯 |
| BFS | queue | O( n2n^2n2 ) | 可以用于最短路 | 从起点开始,搜索相邻的;再以相邻的位起点,继续 |
这里用两个图来形象的模拟过程
深搜——一条路走到黑

广搜——眼观八方

2.DFS
-
每一个DFS都对应一个搜索树;
-
DFS俗称暴搜,其中有顺序的,经常用到DFS;
-
回溯的时候一定要恢复现场;
-
剪枝就是判断出来当前的方案不合法,不再继续往下深搜,直接回溯;
只说知识,有点抽象,根据两个题来理解一下。
2.1 排列数字
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数 n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例:
3输出样例:
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1
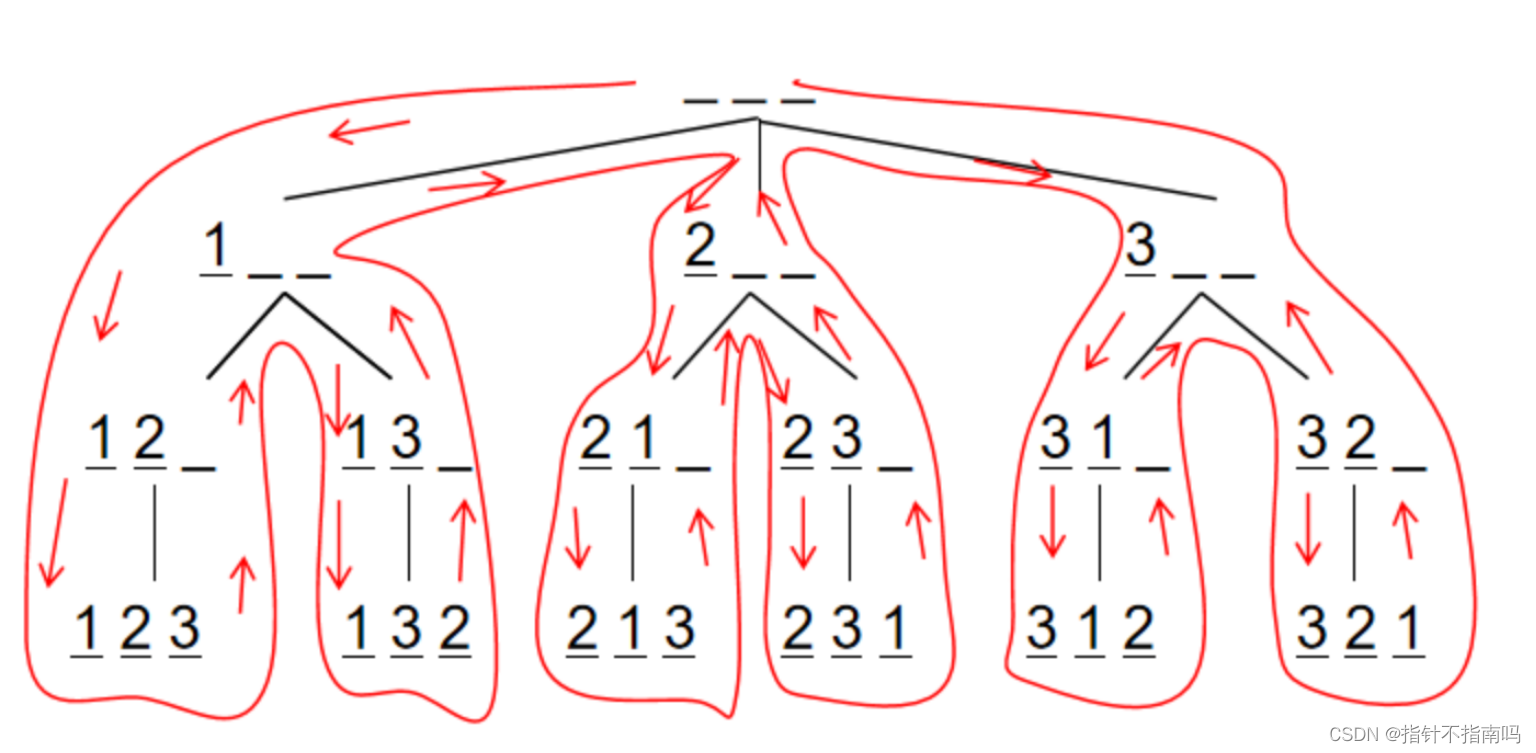
- 思路
图转自acwing以3的全排列为例
-
代码实现
#include<bits/stdc++.h> using namespace std;int n; int path[10];// path 数组保存排列,当排列的长度为 n 时,是一种方案,输出 bool st[10];//st 数组表示数字是否用过:当 st[i] 为 1 时,i 已经被用过,否则 没有被用过void dfs(int u) //dfs(u) 表示:在 path[i] 处填写数字,然后递归的在下一个 u 位置填写数字 {if(u==n){for(int i=0;i<n;i++) cout<<path[i]<<' '; //是一种方案输出cout<<endl;return ;}for(int i=1;i<=n;i++){if(!st[i]) //i 没有被使用过,现在使用{st[i]=true; //状态 改成使用过path[u]=i; //在方案中填上这个数dfs(u+1); //填下一个位置上的数st[i]=false; //回溯:第 i 个位置填写某个数字的所有情况都遍历后, 第 i 个位置填写下一个数字}} }int main() {cin>>n;dfs(0); //从第0个位置上,开始递归,搜索return 0; }
2.2 n-皇后问题
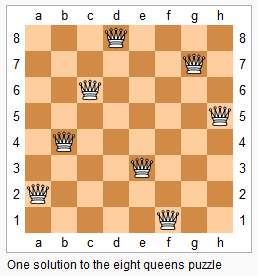
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输入格式
共一行,包含整数 n。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中
.表示某一个位置的方格状态为空,Q表示某一个位置的方格上摆着皇后。每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
数据范围
1≤n≤9
输入样例:
4输出样例:
.Q.. ...Q Q... ..Q...Q. Q... ...Q .Q..
方法一
-
思路
棋盘皇后这个题,和数的全排列很相似
按行枚举,枚举的时候,就保证了行不会重复;
开始放置棋子,第
u行第i列 看看是否可以放皇后,可以就放,递归下一行u+1直到最后,全部 n 个皇后放上棋盘
图解如下
图转自acwing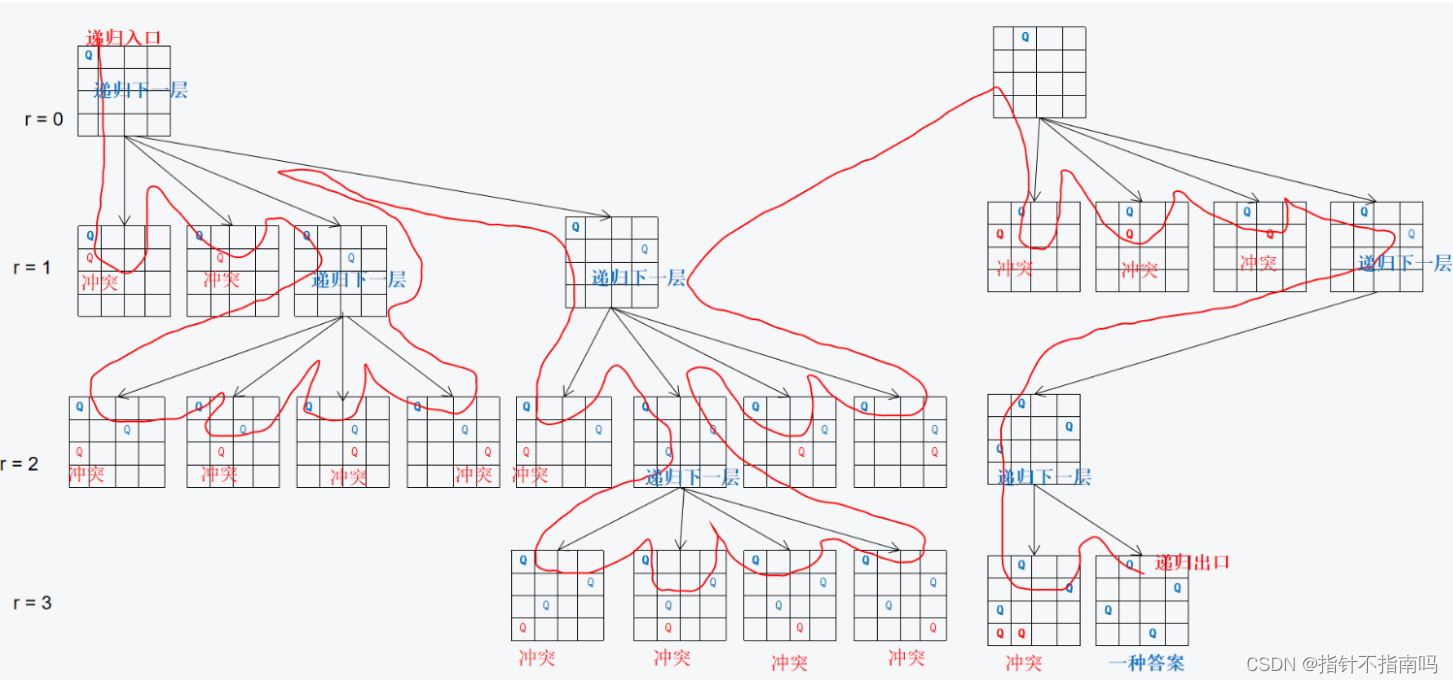
-
代码实现
#include<bits/stdc++.h> using namespace std;int n; const int N=20; char q[N][N]; //存储棋盘 bool cor[N],dg[2*N],udg[2*N]; //cor表示每一列,dg和udg表示正对角线和反对角线,来存储他们的是否被使用过的状态 void dfs(int u) //放第 u 行的棋子 (深度优先遍历) {if(u==n) //如果放盘,则输出棋盘{for(int i=0;i<n;i++){for(int j=0;j<n;j++)cout<<q[i][j];cout<<endl;}cout<<endl;return ; //重点!! 递归到最深层,返回,千万别忘记}for(int i=0;i<n;i++) //从第一列,开始遍历,是否放棋{if(!col[i]&&!dg[i+u]&&!udg[n-i+u]) //如果 列,对角线,没有被放过,则放皇后{q[u][i]='Q'; //放上col[i]=dg[i+u]=udg[n-i+u]=true; //改变状态,dg[i+u]表示截距,每个对角线,都有自己独有的截距;反对角线的截距是负数,数组的下标,不能存放负数,所以加上 n这个偏移量dfs(u+1); //放下一行的col[i]=dg[i+u]=udg[n-i+u]=false; //恢复现场q[u][i]='.';}} }int main() {cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)q[i][j]='.'; //初始化棋盘dfs(0); //从第0行,开始放棋子return 0; }
方法二
-
思路
枚举 每一个位置的棋子
每个位置可以分成两种情况:放
Q不放Q把每一种情况都枚举出来
-
代码实现
#include<bits/stdc++.h> using namespace std;int n; const int N=20; char q[N][N]; bool row[N], col[N],dg[N],udg[N];void dfs(int x,int y,int s) //x表示行,y表示列,s表示已经放上皇后的个数 {//处理超边界地情况if(y==n) y=0,x++; if(x==n) //每个位置都枚举完了{if(s==n) // n 个皇后都放上去了{for(int i=0;i<n;i++)puts(q[i]); //输出棋盘, q[i],传的是数组指针,输出的是一整行puts("");}return ; //递归到最后返回}//分支1,不放皇后dfs(x,y+1,s);//分支2,放皇后if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[n-x+y]){q[x][y]='Q';row[x]=col[y]=dg[x+y]=udg[n-x+y]=true;dfs(x,y+1,s+1);row[x]=col[y]=dg[x+y]=udg[n-x+y]=false;q[x][y]='.';}}int main() {cin>>n;for(int i=0;i<n;i++)for(int j=0;j<n;j++)q[i][j]='.';dfs(0,0,0);return 0; }
3.BFS
比较简单,一般模板可以直接解决
直接上例题,来理解一下
3.1走迷宫
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 00 或 11,其中 00 表示可以走的路,11 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1)处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0输出样例:
8
-
思路
从起点开始,遍历每一个位置,
看他四个方向,是否满足条件,满足条件的,走它,
在看它的四个方向是否满足条件,满足走它
每走一步,距离+1,
最后返回 走到 终点 的距离
图解如下
图转自acwing
-
代码实现
#include<bits/stdc++.h> using namespace std;typedef pair<int ,int> PII; //定义 坐标const int N=110;int n,m; int g[N][N]; //表示地图 int d[N][N]; //存的是某一点到源点的距离int dfs() {queue<PII> q; //定义队列,里面存的表示我们将要走的哪一个点q.push({0,0}); //先把放进去,表示我们要走 起点memset(d,-1,sizeof d); //初始化,把每个点到源点的距离初始化为 -1d[0][0]=0; //源点到自己的距离为0int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0}; //我们定义的四个方向 x,y 的移动,这样可以避免 4个判断语句,注意 dx,dy 要一一对应//从第一个开始位置开始遍历while(!q.empty()) //走到最后{auto t=q.front(); //把队列中的第一个元素取出来q.pop(); //对头元素出列for(int i=0;i<4;i++){int x=t.first+dx[i],y=t.second+dy[i]; //扩展之后的坐标//x,y不能越界,可以走,没走过if(x>=0&&x<n&&y>=0&&y<m&&g[t.first][t.second]==0&&d[x][y]==-1){d[x][y]=d[t.first][t.second]+1; //距离+1q.push({x,y}); //把把满足条件地坐标插进去,下一次走它们}}}return d[n-1][m-1]; //返回最后一个即终点到源点地距离 }int main() {cin>>n>>m;for(int i=0;i<n;i++)for(int j=0;j<m;j++)cin>>g[i][j]; //读入地图cout<<dfs()<<endl;return 0; }