归并排序本质上可以看作二叉树的后序遍历

里面用到的核心思想 => 分治

分：二叉树算法思想中的分解问题思想

治：链表中双指针技巧（将两条链表合并成一条有序链表）

sort首先将数组分成左半边和右半边 

=> 然后分别对左右两边再sort（递归的味道）

=>最后通过merge合并左右两边数组

将问题无限细分下去，至不能再分解（base返回），好这就到底了

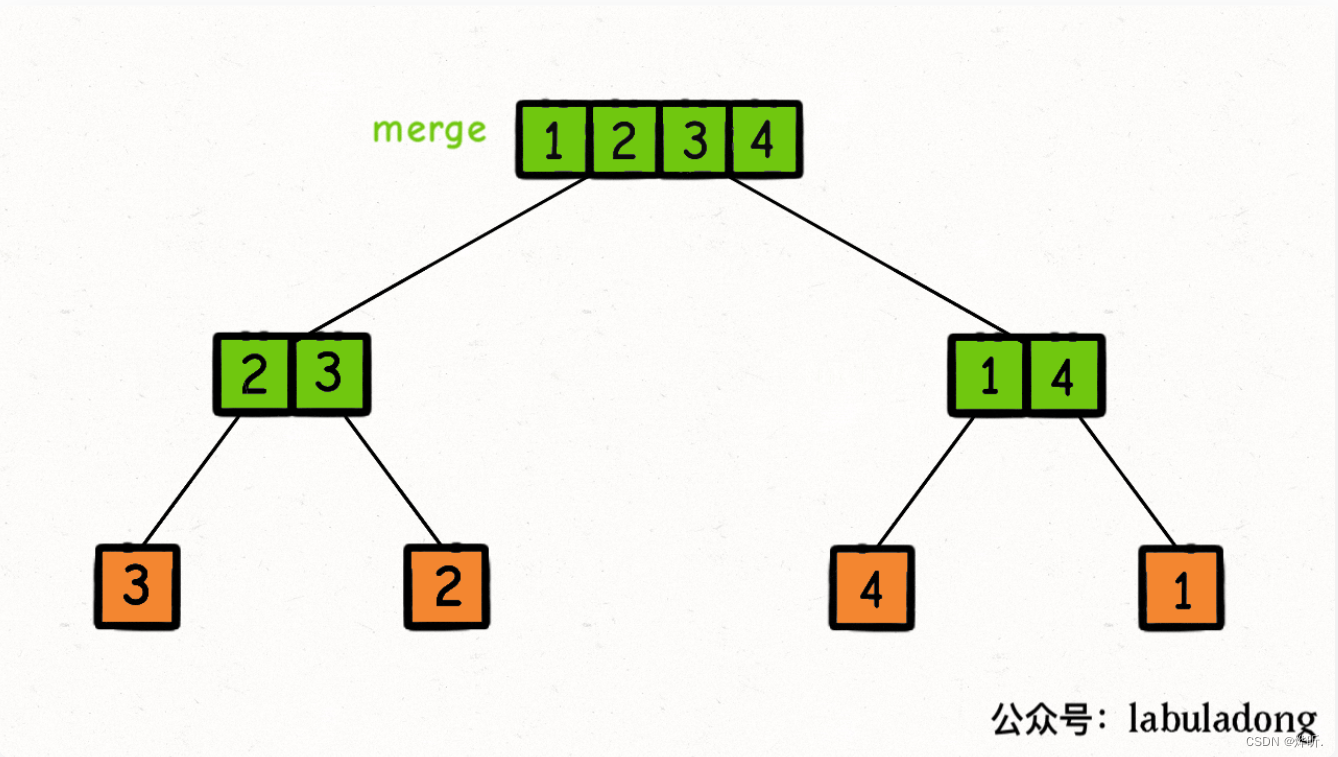
开始向上返回，在向上返回的过程中不断的merge，直至顶部完成任务

放张图辅助理解一下，也帮作者推广一下

归并排序

class Merge {
private:vector<int> temp;
public:void sort(vector<int>& nums) {temp.resize(nums.size());sort(nums, 0, nums.size() - 1);}
private:void sort(vector<int>& nums, int left, int right) {if(left == right) return;int mid = left + (right - left) / 2;sort(nums, left, mid);sort(nums, mid + 1, right);merge(nums, left, mid, right);}void merge(vector<int>& nums, int left, int mid, int right) {for(int i = left; i <= right; i++) {temp[i] = nums[i];}int p1 = left, p2 = mid + 1;for(int i = left; i <= right; i++) {if(p1 == mid + 1) nums[i] = temp[p2++];else if(p2 == right + 1) nums[i] = temp[p1++];else if(temp[p1] < temp[p2]) nums[i] = temp[p1++];else if(temp[p1] > temp[p2]) nums[i] = temp[p2++];}}
};int main() {vector<int> nums;int n;cin >> n;while(n--) {int num;cin >> num;nums.emplace_back(num);}(new Merge())->sort(nums);for(auto num: nums) {cout << num << " ";}return 0;
}

归并排序拓展应用

315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）

这题和归并排序的关系 => 主要在 merge 函数，我们在使用 merge 函数合并两个有序数组的时候，其实是可以知道一个元素 nums[i] 后边有多少个元素比 nums[i] 小的。

因为在层层向上merge的时候每个子数组都是有序的

class Solution {
public: vector<pair<int,int>> help;vector<int> count;vector<int> countSmaller(vector<int>& nums) {int n = nums.size();help.resize(n);count.resize(n);vector<pair<int,int>> arr;for(int i=0;i<n;i++){pair<int,int> temp(i, nums[i]);arr.push_back(temp);}process(arr,0,n-1);return count;}void process(vector<pair<int,int>>& arr,int left,int right){if(left==right) return;int mid = left+(right-left)/2;process(arr,left,mid);process(arr,mid+1,right);merge(arr,left,mid,right);}void merge(vector<pair<int,int>>& arr,int left,int mid,int right){for(int i=left;i<=right;i++){help[i] = arr[i];}int i = left, j = mid+1;for(int p=left;p<=right;p++){if(i==mid+1) arr[p] = help[j++];else if(j==right+1){arr[p] = help[i++];count[arr[p].first] += j-mid-1;}else if(help[i].second>help[j].second) arr[p] = help[j++];else{arr[p] = help[i++];count[arr[p].first] += j-mid-1;}}}
};