网站导航
> 文章列表 > DFIG控制9： 搭建定子αβ坐标系下的电机模型

DFIG控制9： 搭建定子αβ坐标系下的电机模型

网友: 文章列表 2024-03-21 22:01:53

DFIG控制9： 搭建定子αβ坐标系下的电机模型

DFIG控制9： 搭建定子αβ坐标系下的电机模型。本文基于教程的第9部分（终于做完了）。主要目的是自己搭建一个DFIG的电机模型，与Simulink库中的模型做个对比。
本文基于教程的第9部分：
DFIM Tutorial 9 - Analytical Model of Doubly Fed Induction Generator for On-Line Simulation 主要目的是自己搭建一个DFIG的电机模型，与Simulink库中的模型做个对比。

教程使用的参考书：
G. Abad, J. Lopez, M. Rodriguez, L. Marroyo, and G. Iwanski, Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation. John Wiley & Sons, 2011.

需要搭建的模型的框图如下：
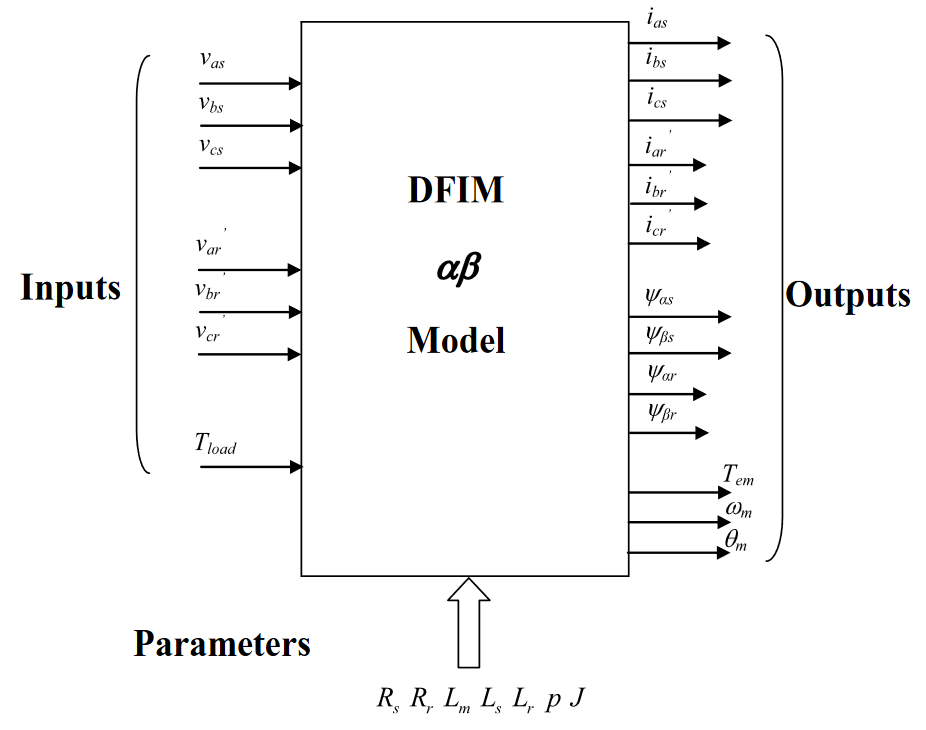
DFIG控制9： 搭建定子αβ坐标系下的电机模型

理论部分

使用 DFIG控制10： 双馈发电机的动态模型 中推导的定子静止αβ坐标系下的电压和磁链方程：

{usα=Rsisα+ddtψsαusβ=Rsisβ+ddtψsβurα=Rrirα+ddtψrα+ωrψrβurβ=Rrirβ+ddtψrβ−ωrψrα\\begin{cases} u_{s\\alpha} &= R_si_{s\\alpha}+\\frac{d}{dt}\\psi_{s\\alpha}\\\\ u_{s\\beta} &= R_si_{s\\beta}+\\frac{d}{dt}\\psi_{s\\beta}\\\\ u_{r\\alpha} &= R_ri_{r\\alpha}+\\frac{d}{dt}\\psi_{r\\alpha}+\\omega_r\\psi_{r\\beta}\\\\ u_{r\\beta} &= R_ri_{r\\beta}+\\frac{d}{dt}\\psi_{r\\beta}-\\omega_r\\psi_{r\\alpha} \\end{cases} ⎩⎨⎧​usα​usβ​urα​urβ​​=Rs​isα​+dtd​ψsα​=Rs​isβ​+dtd​ψsβ​=Rr​irα​+dtd​ψrα​+ωr​ψrβ​=Rr​irβ​+dtd​ψrβ​−ωr​ψrα​​
{ψsα=(1.5Lm+Lls)isα+1.5Lmirα=Lsisα+LMirαψsβ=(1.5Lm+Lls)isβ+1.5Lmirβ=Lsisβ+LMirβψrα=(1.5Lm+Llr)irα+1.5Lmisα=Lrirα+LMisαψrβ=(1.5Lm+Llr)irβ+1.5Lmisβ=Lrirβ+LMisβ\\begin{cases} \\psi_{s\\alpha} &= (1.5L_m+L_{ls})i_{s\\alpha}+1.5L_mi_{r\\alpha} =L_si_{s\\alpha}+L_Mi_{r\\alpha}\\\\ \\psi_{s\\beta} &= (1.5L_m+L_{ls})i_{s\\beta}+1.5L_mi_{r\\beta} =L_si_{s\\beta}+L_Mi_{r\\beta}\\\\ \\psi_{r\\alpha} &= (1.5L_m+L_{lr})i_{r\\alpha}+1.5L_mi_{s\\alpha} =L_ri_{r\\alpha}+L_Mi_{s\\alpha}\\\\ \\psi_{r\\beta} &= (1.5L_m+L_{lr})i_{r\\beta}+1.5L_mi_{s\\beta} =L_ri_{r\\beta}+L_Mi_{s\\beta} \\end{cases} ⎩⎨⎧​ψsα​ψsβ​ψrα​ψrβ​​=(1.5Lm​+Lls​)isα​+1.5Lm​irα​=Ls​isα​+LM​irα​=(1.5Lm​+Lls​)isβ​+1.5Lm​irβ​=Ls​isβ​+LM​irβ​=(1.5Lm​+Llr​)irα​+1.5Lm​isα​=Lr​irα​+LM​isα​=(1.5Lm​+Llr​)irβ​+1.5Lm​isβ​=Lr​irβ​+LM​isβ​​
这里有4个关于磁链的微分方程，加上转矩和转子机械角频率的关系，模型共有5个微分方程。
写成矩阵形式，再消去电流，如下：

u=Ri+ddtψ+Aψψ=Li→ddtψ=−(RL−1+A)ψ+u\\begin{align*} \\boldsymbol{u} &= \\boldsymbol{R}\\boldsymbol{i}+ \\frac{d}{dt}\\boldsymbol{\\psi} +A\\boldsymbol{\\psi}\\\\ \\boldsymbol{\\psi} &= \\boldsymbol{L}\\boldsymbol{i}\\\\ \\rightarrow \\frac{d}{dt}\\boldsymbol{\\psi}&= -(\\boldsymbol{R}\\boldsymbol{L}^{-1}+\\boldsymbol{A})\\boldsymbol{\\psi}+\\boldsymbol{u} \\end{align*} uψ→dtd​ψ​=Ri+dtd​ψ+Aψ=Li=−(RL−1+A)ψ+u​

其中，
R=[Rs0000Rr0000Rr0000Rr]L=[Ls0LM00Ls0LMLM0Lr00LM0Lr]A=[00000000000ωr00−ωr0]\\begin{align*} \\boldsymbol{R}&= \\left[\\begin{matrix} R_{s} &0 &0 &0 \\\\ 0 & R_{r} &0 &0\\\\ 0 &0 &R_{r} &0\\\\ 0 &0 &0 &R_{r} \\end{matrix}\\right]\\\\ \\boldsymbol{L}&= \\left[\\begin{matrix} L_{s} &0 &L_{M} &0 \\\\ 0 & L_{s} &0 &L_{M}\\\\ L_{M} &0 &L_{r} &0\\\\ 0 &L_{M} &0 &L_{r} \\end{matrix}\\right]\\\\ \\boldsymbol{A}&= \\left[\\begin{matrix} 0 &0 &0 &0 \\\\ 0 & 0 &0 &0\\\\ 0 &0 &0 &\\omega_{r}\\\\ 0 &0 &-\\omega_{r} &0 \\end{matrix}\\right] \\end{align*} RLA​=​Rs​000​0Rr​00​00Rr​0​000Rr​​​=​Ls​0LM​0​0Ls​0LM​​LM​0Lr​0​0LM​0Lr​​​=​0000​0000​000−ωr​​00ωr​0​​​
并且令漏感系数为：
σ=1−LM2LsLr\\sigma=1- \\frac{L_{M}^{2}}{L_{s}L_{r}}σ=1−Ls​Lr​LM2​​

在MathCAD中计算 −(RL−1+A)-(\\boldsymbol{R}\\boldsymbol{L}^{-1}+\\boldsymbol{A})−(RL−1+A)：
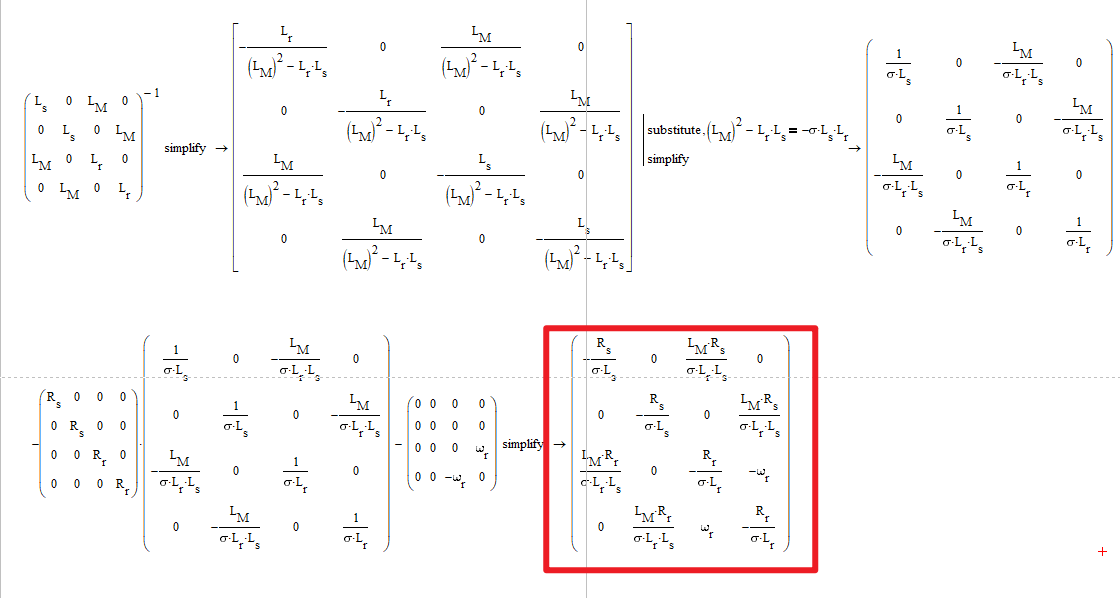
DFIG控制9： 搭建定子αβ坐标系下的电机模型

最终，用于仿真的模型为：
{ddt[ψsαψsβψrαψrβ]=[−RsσLs0LMRsσLrLs00−RsσLs0LMRsσLrLsLMRrσLrLs0−RrσLr−ωr0LMRrσLrLsωr−RrσLr][ψsαψsβψrαψrβ]+[usαusβurαurβ]Jpdωrdt=Te−TL\\begin{cases} \\frac{d}{dt} \\left[\\begin{matrix} \\psi_{s\\alpha} \\\\ \\psi_{s\\beta} \\\\ \\psi_{r\\alpha} \\\\ \\psi_{r\\beta} \\end{matrix}\\right]= \\left[\\begin{matrix} \\frac{-R_{s}}{\\sigma L_{s}} & 0 & \\frac{L_{M}R_{s}}{\\sigma L_{r}L_{s}} & 0 \\\\ 0 & \\frac{-R_{s}}{\\sigma L_{s}} & 0 & \\frac{L_{M}R_{s}}{\\sigma L_{r}L_{s}} \\\\ \\frac{L_{M}R_{r}}{\\sigma L_{r}L_{s}} & 0 & \\frac{-R_{r}}{\\sigma L_{r}} & -\\omega_{r} \\\\ 0 & \\frac{L_{M}R_{r}}{\\sigma L_{r}L_{s}} & \\omega_{r} & \\frac{-R_{r}}{\\sigma L_{r}} \\\\ \\end{matrix}\\right] \\left[\\begin{matrix} \\psi_{s\\alpha} \\\\ \\psi_{s\\beta} \\\\ \\psi_{r\\alpha} \\\\ \\psi_{r\\beta} \\end{matrix}\\right] +\\left[\\begin{matrix} u_{s\\alpha} \\\\ u_{s\\beta} \\\\ u_{r\\alpha} \\\\ u_{r\\beta} \\end{matrix}\\right] \\\\ \\frac{J}{p}\\frac{d \\omega_{r}}{dt}=T_{e}-T_{L} \\end{cases} ⎩⎨⎧​dtd​​ψsα​ψsβ​ψrα​ψrβ​​​=​σLs​−Rs​​0σLr​Ls​LM​Rr​​0​0σLs​−Rs​​0σLr​Ls​LM​Rr​​​σLr​Ls​LM​Rs​​0σLr​−Rr​​ωr​​0σLr​Ls​LM​Rs​​−ωr​σLr​−Rr​​​​​ψsα​ψsβ​ψrα​ψrβ​​​+​usα​usβ​urα​urβ​​​pJ​dtdωr​​=Te​−TL​​
p为极对数，仿真中p=2。

电机仿真模型搭建

仿真中使用磁链来计算电磁转矩。
Te=32pLMσLsLr(ψsβψrα−ψsαψrβ)T_{e}=\\frac{3}{2}p \\frac{L_{M}}{\\sigma L_{s}L_{r}}(\\psi_{s \\beta}\\psi_{r \\alpha}-\\psi_{s \\alpha}\\psi_{r \\beta}) Te​=23​pσLs​Lr​LM​​(ψsβ​ψrα​−ψsα​ψrβ​)
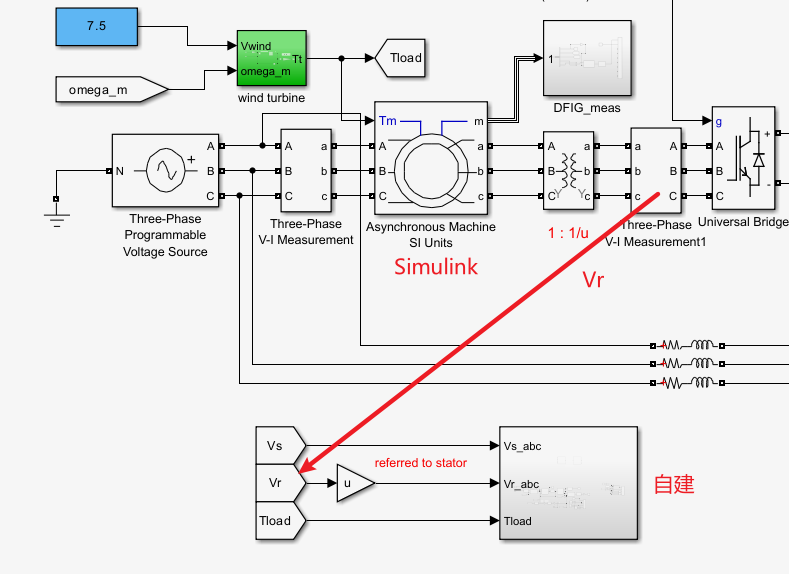
自己搭建仿真模型如下：

  1. 因为是定子αβ坐标系下的模型，
    1. 需要对输入的定子电压做Clarke变换
    2. 对输入的转子电压，先做Clarke变换，再做坐标系旋转。
    3. 对输出的定子电流，做Clarke反变换，得到定子ABC电流
    4. 对输出的转子电流，先做坐标系旋转，再做Clarke反变换转子abc电流
  2. 转子电压和Simulink模型使用相同的输入，都是，考虑了变压器的变比。
  3. ddtψ\\frac{d}{dt}\\boldsymbol{\\psi}dtd​ψ 4个方程的计算，然后通过积分得到4个磁链的参数
  4. 基于磁链值，计算电流和电磁转矩
  5. 电磁转矩和机械转矩做差，然后积分，得到机械转速（上面模型的第5个方程）。再积分，得到转子的机械角度和电角度。

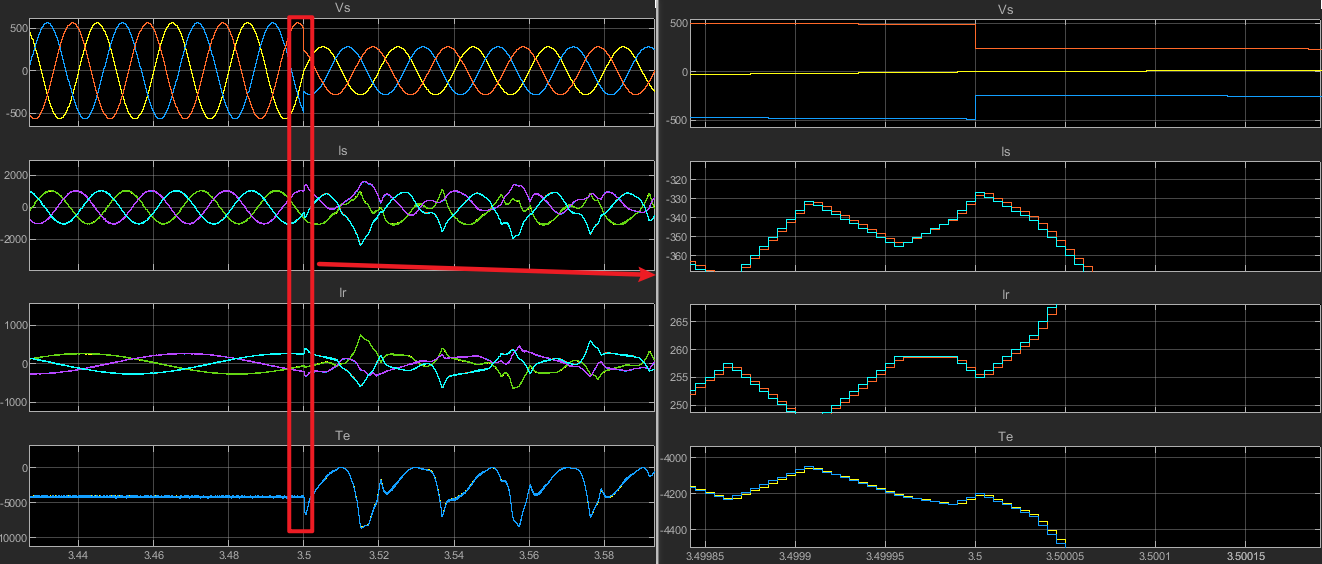
DFIG控制9： 搭建定子αβ坐标系下的电机模型
DFIG控制9： 搭建定子αβ坐标系下的电机模型

仿真对比

上方信号来自Simulink模型，下方带_m的信号来自刚才搭的模型。
自己搭的模型，输出的定子电流、转子电流、转矩，和Simulink模型基本相同。电网电压跌落期间的暂态波形也基本一致。但是放大后可以看到差异。

DFIG控制9： 搭建定子αβ坐标系下的电机模型

DFIG控制9： 搭建定子αβ坐标系下的电机模型

剩余问题

  1. 自己搭的模型，在跑较长时间以后（10s左右），输出会发散，波形就和Simulink的模型不一致了，（不知道教程里面的模型是不是也这样，感觉可能是我模型里面一些模块的设置问题）

初始化代码

clear% DFIG parameters -> Rotor parameters referred to the stator side
f = 50; % Stator frequency (Hz)
Ps = 2e6; % Rated stator power (W)
n = 1500; % Rated rotational speed (rev/min)
Vs = 690; % Rated stator voltage (V)
Is = 1760; % Rated stator current (A)
Tem = 12732; % Rated torque (N.m)p=2; % Pole pairu = 1/3; % Stator/rotor turns ratio
Vr = 2070;    % Rated rotor voltage (non-reached) (V) 
smax = 1/3;   % Maximum slip
Vr_stator = (Vr*smax) *u;    % Rated rotor voltage referred to stator (V)
Rs = 2.6e-3;    % Stator resistance(ohm)                
Lsi = 0.087e-3; %  Leakage inductance (stator & rotor) (H)                 
Lm = 2.5e-3; %  Magnetizing inductance (H)
Rr = 2.9e-3; % Rotor resistance referred to stator (ohm)
Ls = Lm + Lsi; % Stator inductance (H)
Lr = Lm + Lsi; % Rotor inductance (H)
% Vbus = Vr_stator*sqrt(2); % DC de bus voltge referred to stator (V)
Vbus = 1150; % as in tutorial 4sigma = 1-Lm^2/(Ls*Lr);Fs = Vs*sqrt(2/3)/(2*pi*f);  % Stator Flux (aprox.) (Wb)
J = 127; % Inertia, originally 127, reduced by 2 to make the response faster
D = 10e-3; %damping = 0. originally D = 1e-3;fsw = 4e3; 
Ts =  1/fsw/50;kT = -1.5*p*(Lm/Ls)*Fs; % kT, coef of output of the speed controller  tau_i = (sigma*Lr)/Rr;
tau_n = 0.05; 
wni = 100*(1/tau_i);
wnn = 1/tau_n;kp_id = (2*wni*sigma*Lr)-Rr;
kp_iq = kp_id;ki_id = (wni^2)*Lr*sigma;
ki_iq = ki_id;kp_n = (2*wnn*J)/p; %kp_n = (2*wnn*J)/p;
ki_n = (wnn^2)*J/p; %ki_n = (wnn^2)*J/p;% Three blade wind turbine mode
N = 100; % Gearbox ratio
Radio= 42; % blade radius 
ro= 1.225; % Air density% Cp and Ct curves
beta=0;  % Pitch angle
ind2=1;for lambda=0.1:0.01:11.8lambdai(ind2)= (1./((1./(lambda-0.02.*beta) + (0.003./ (beta^3+1)))));Cp(ind2)=0.73*(151./lambdai(ind2) - 0.58*beta - 0.002.*beta^2.14-13.2).*(exp(-18.4./lambdai (ind2))); Ct(ind2)=Cp(ind2)/lambda;ind2=ind2+1;
endtab_lambda=[0.1:0.01:11.8];% Kopt for MPPT
Cp_max = 0.44; 
lambda_opt = 7.2;
Kopt = ((0.5*ro*pi* (Radio^5) *Cp_max)/(lambda_opt^3));
% Power curve in fucntion of wind speedP = 1.0e+06 *[0,0,0,0,0,0,0,0.0472,0.1097,0.1815,0.2568,0.3418, ...0.4437,0.5642, 0.7046, 0.8667,1.0518,1.2616, 1.4976, 1.7613,2.0534,...2.3513,2.4024,2.4024,2.4024, 2.4024,2.4024,2.4024];
V = [0.0000,0.5556,1.1111,1.6667,2.2222,2.7778,3.3333,3.8889, 4.4444,... 5.0000,5.5556,6.1111,6.6667,7.2222,7.7778,8.3333,8.8889,9.4444, ...10.0000,10.5556,11.1111, 11.6667,12.2222,12.7778,13.3333, 13.8889,...14.4444,15.0000];
% figure
% subplot(1,2,1)
% plot(tab_lambda, Ct, 'linewidth',1.5)
% xlabel('\\lambda', 'fontsize',14)
% ylabel('Ct', 'fontsize',14)
% subplot(1,2,2)
% plot (V, P, 'linewidth', 1.5)
% grid
% xlabel('Wind speed (m/s)', 'fontsize',14)
% ylabel('Power (W)', 'fontsize',14)% Grid side converter
Cbus = 80e-3; % DC bus capacitance
Rg = 20e-6; % Grid side filter's resisatance
Lg = 400e-6; % Grid side filter's inductance
Kpg = 1/(1.5*Vs*sqrt(2/3));
Kqg = -Kpg;% PI regulators
tau_ig = Lg/Rg;
wnig = 60*2*pi;kp_idg = (2*wnig*Lg)-Rg;
kp_iqg = kp_idg; 
ki_idg = (wnig^2)*Lg;
ki_iqg = ki_idg;kp_v = -1000;
ki_v = -300000; %ki_v = -300000;Rcrowbar = 0.2; % crowbar circuit resistance
Tcrowbar = 0.1; % crowbar duration 0.1st_dip= 3;
t_recover = 3.5;
t_normal = 4.17;a11 = -Rs/(sigma*Ls);
a22 = a11;
a33 = -Rr/(sigma*Lr);
a44 = a33;
a13 = Rs*Lm/(sigma*Ls*Lr);
a24 = a13;
a31 = Rr*Lm/(sigma*Ls*Lr);
a42 = a31;
A = [a11, 0, a13, 0;0, a22, 0, a24;a31, 0, a33, 0;0, a42, 0, a44];% A = [a11, 0, a13, 0;
%     0, a11, 0, a13;
%     a31, 0, a33, 0;
%     0, a31, 0, a33];
网络标签：

相关问题