线性代数 --- Gram-Schmidt, 格拉姆-施密特正交化（上）

        在求解最小二乘的问题时，已经介绍了类似于Gram-Schmidt的一些想法。在这里要继续介绍这些想法，那就是如何“改写”矩阵A中的列向量，使得最小二乘解的计算越来越简单，甚至可以直接写出答案。

标准正交基(Orthonormal Bases)

        上一篇文章中，我们结束在三个观测点分别在t=(1,3,5)这三个时刻所得到的观测值b1,b2,b3的最小二乘直线拟合b=C+Dt。当时，我们为了让正规方程更好解，通过把t减去他的均值3，得到T=t-3=(-2,0,2)，实现了最小二乘解的快速求解(即不是简单的通过套用公式来计算，而是直接求解正规方程，这样一来，也避免了求的逆，这种精度误差较大的运算)。

        首先，对于三个数据点(t1=1,b1=1),(t2=3,b2=2),(t3=5,b3=4)而言，因A的两个列向量不是正交的，不是对角阵，所以，最好通过公式来计算。

         矩阵A的两个列向量的内积不为0，不正交。且不是对角阵。后面，我们为了让变成对角阵，把t=(1,3,5)变成了T=(-2,0,2), 也变成了对角阵。

        更进一步，如果我们把A中的两个彼此正交的列向量(orthogonal vectors)都变成单位正交向量(orthogonal unit vectors)，则会从对角阵变成单位矩阵I。把一个向量变成单位向量的办法是除以这个向量自身的长度。

根据向量长度的计算公式有，列向量col1的长度为根号3，col2的长度为根号8，归一化后有：

得到单位化后的新矩阵：

和新的方程(注意为了维持原方程组Ax=b中的A变成后，方程左右两边保持不变，原方程中的x也要改变，变成)：

用这个新矩阵去计算正规方程中的得到单位矩阵I：

正规方程左边：

最终得到全新的正规方程，这是一个一眼就能得到答案的全新方程组，因为为方阵，使得原来的正规方程变成：

最终得到了和原来一样的答案：

        在本例中，归一化后的两个相互正交的列向量和就是一组标准正交基。现在，我们给出关于标准正交基Orthonormal的正式定义：

        如果一组列向量，他们满足彼此之间的内积为0（满足了正交性），且，自己的长度为1（满足了单位化）。则，我们把这样的一组列向量称为标准正交基Orthonomal。同时，我们也把由标准正交基组成的矩阵用大写的英文字母Q来表示。

        对于标准正交基而言，一个最常见的例子就是x-y二维坐标系，q1=(1,0)，q2=(0,1)。我们这两个坐标轴不仅垂直，而且，我们还在坐标轴上分别用单位长度标出了每一个刻度。q1和q2共同组成了一个2x2矩阵Q，这是一个2x2的单位矩阵。

        对于n维空间，同样有n个坐标轴e1,e2,....en，他们也是一组标准正交基，且他们所组成的矩阵Q也是一个单位阵。

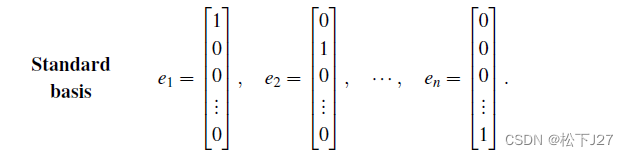
标准正交矩阵(Orthogonal Matrices)

        我们把用标准正交基q1,q2...qn所组成的矩阵称为标准正交矩阵Q，Q可以是方阵也可以不是方阵。且，。

         如果标准正交矩阵Q是一个方阵的话，则这个方阵是满秩的，且秩r=n。则有：

也就是说，如果Q是一个标准正交矩阵，则也是一个标准正交矩阵。

例：任何置换矩阵P（permutation）都是一个标准正交矩阵。

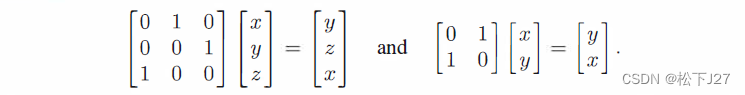
         上图的两个置换矩阵，分别交换了(x,y,z)的位置和交换了(x,y)的位置。因为，这两个置换矩阵P的列向量都是单位向量，且彼此两两正交。所以也是标准正交矩阵。

最后，在这里补充一条标准正交矩阵Q的又一条重要性质，即，用一个标准正交矩阵Q去乘一个任意向量都不会改变这个向量的长度。（书上上，这一性质还挺重要的，只是我暂时没发现）

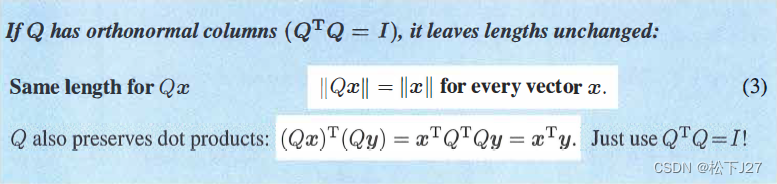
当A为标准正交矩阵时的投影与最小二乘

        对于一个mxn的矩阵A，如果矩阵A中的列向量都彼此正交，且向量长度都是1。则A是一个标准正交矩阵。若方程组Ax=b，无解则需要根据最小二乘的计算公式分别计算和。但如果A是标准正交矩阵Q的话，或者说，如果我们先把矩阵A变成标准正交矩阵的话，就能极大的简化最小二乘的计算。

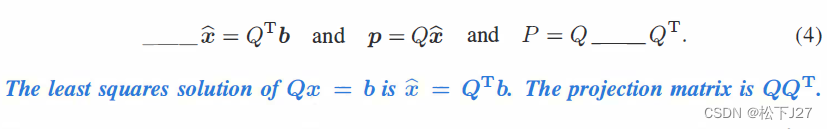
 第一：他极大地简化了正规方程的表达式，同时，直接给出了最小二乘解。

（正规方程）

第二：他简化了所有包含的计算，同时，更重要的是他也避免了求的逆。

（投影）

 （投影矩阵）

        在代数表达式得到改进的同时，几何表示也得到了相应的改进。根据向量的投影，投影变成了：

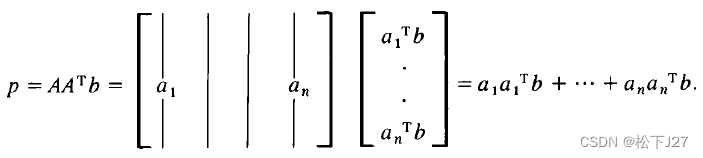
 其中：

           依此类推。。。

令b=(b1,b2,...,bn),则有：

         依此类推。。。

用几何图像来表示就是：

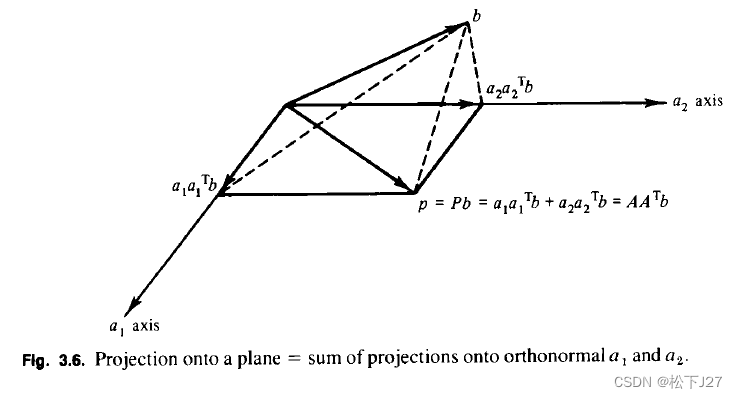
也就是说，向量b在A所张成的列空间上的投影p等于，b在每个坐标轴上的投影的和。

        此外，当A为标准正交矩阵时（当A为方阵时,m=n），A中的列向量可以张满整个。A中的每个列向量，实际上就是n维正交坐标系中的每个轴所对应的单位向量。对于中的任意一个向量b，b在A的列空间内，所以可以写成Ax=b的形式，x中的每个元素都是A中各列所对应的权重。当A为Q时，我们把Qx=b写成如下形式：

q1,q2,...,qn分别表示n维坐标系中的每个坐标轴上的单位向量，这样一来，上式所表示的就是，在n维直角坐标系中，任意一个向量b等于，他在q1轴，q2轴，。。。qn轴上分量的和。

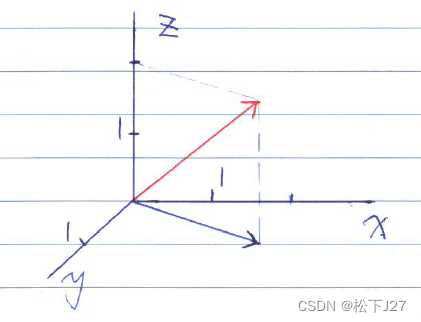
例如：

当x=1.5,y=1,z=2时有。

小结：

1,        给定的mxn方程组 Ax=b 无解

2,        左右两边同时乘以,得到正规方程

3,        求解正规方程，得到

4,        若A是一个标准正交矩阵Q，则有，Qx=b

5,        左右两边同时乘以,得到新的正规方程

6,        因为，极大了简化正规方程，得到

7,        与此同时，也简化了投影p的计算，得到

 （全文完）

作者 --- 松下J27

参考文献(鸣谢)：

1，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang

2，线性代数及其应用，候自新，南开大学出版社 1990

3，Linear Algebra and Its Applications, Second Edition, Gilbert Strang, 1980

4，Linear Algebra and Its Applications, Fourth Edition, Gilbert Strang, 2005

（配图与本文无关）

版权声明：文中的部分图片，文字或者其他素材，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27