网站导航
> 文章列表 > 拉曼光谱的airPLS处理算法原理及MATLAB示例

拉曼光谱的airPLS处理算法原理及MATLAB示例

网友: 文章列表 2024-03-21 21:41:46

拉曼光谱的airPLS处理算法原理及MATLAB示例

  一、拉曼光谱及airPLS算法

        拉曼光谱被称作物质的“指纹谱”，能够表征分子的特征官能团，具有极高的特异性，在检测传感领域有极大的应用前景。但拉曼散射强度低，在实际的检测应用过程中还会受到噪声的影响。    

        为减少拉曼光谱中的噪声影响，可利用airPLS--自适应迭代重加权惩罚最小二乘法可用于背景噪声的扣除[1]。此方法已经被广泛的应用，它能有效扣除噪声，保留拉曼光谱的有效信息，增加拉曼光谱的信噪比。

二、airPLS算法原理

        自适应迭代重加权惩罚最小二乘法主要可以分为两步。

（1）惩罚最小二乘算法

        此方法是一种曲线平滑方法，可以平衡原始数据准确度和拟合数据的粗糙度。假设x是原始光谱矢量（光谱数据的原始峰值），z是拟合矢量（拟合后的光谱峰值），长度均为m（光谱数据的横坐标），z对x的准确度可以表示为两者间的平方差总和F，拟合数据z的粗糙度可以表示为相邻两项之间平方和R，两者的计算公式为：

{\\color{Red} }F=\\sum_{i=1}^{m}(x_{i}-z{_{i}})^{^{2}}

 R=\\sum_{i=2}^{m}(z_{i}-z_{i-1}){^{2}}

        可以看出，F越大，拟合曲线的值越接近真实值，R值越大拟合曲线的粗糙度越大，偏离真实值，但曲线光滑性越好。此公式为一阶差分惩罚项，该算法在实际应用中可以选择差分惩罚项的阶数，一段二阶为比较常用的。准确度与粗糙度两者相互对立，两者如何平衡是解决问题的关键。在这里，以Q为平衡参数，来表述拟合曲线的特征，其值为准确度与惩罚后的粗糙度之和。

Q=F+\\lambda\\cdot R

其中，\\lambda可以调节，其值越大，表示粗糙度占比越大，拟合曲线越光滑。

（2）自适应迭代重加权法

        自适应迭代重加权法的引入是为了计算权重，增加惩罚项来调整拟合基线的平滑度，迭代的每一步都要计算加权惩罚最小二乘式 Q^{t}。

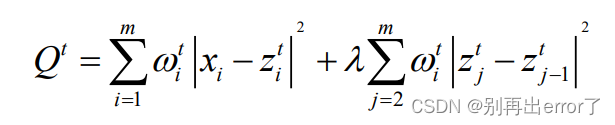
其中，t 是迭代次数，加权矢量 w 初始值为0（w相当于针对每个数据增强一个权重）， 其迭代公式为：

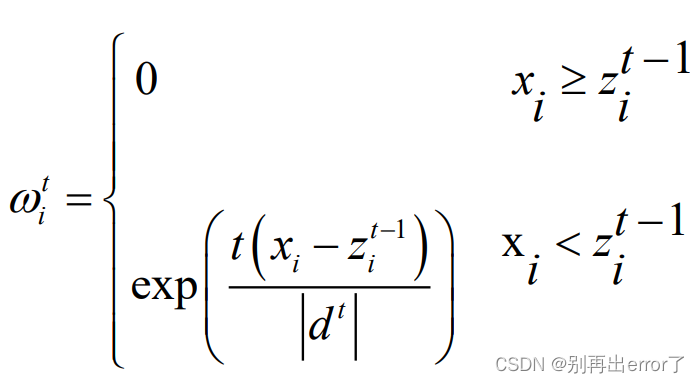
         其中，d^{t} 是第 t 次迭代矢量 x 与 z^{t-1} 之差小于0的部分组成。前一次迭代的拟合值 z^{t-1} 作为基线的参考值，如果第 i 个点的值比基线参考值大，则被认为是峰的一部分，此时权重被设为0，在拟合的下次迭代忽略。

        此方法用来自动去除各个峰包含的点，保留加权矢量 w 的基线点，就能拟合出原始光谱的背景信号，再利用原始光谱与之相减，即可得到有效的拉曼光谱数据。迭代在到达最大迭代次数或满足 \\left | d \\right |< 0.001\\cdot \\left | x \\right | 。

 三、MATLAB示例

（1）MATLAB代码：  

airPLS算法处理拉曼光谱数据流程：

clear
close allA=xlsread('221031.xlsx','Sheet1');
xx=A(100:900,1);   %%%%% 拉曼偏移 x
xx=xx';
x1=A(100:900,3);    %%%%% 拉曼强度 y
x1=x1';
%x=p3;
lambda1=10e2; %%%%% 平滑程度 待修改
[xbc1,xb1]=airPLS(x1, lambda1,2,0.1,0.5,20);
figure
plot(xx,x1,'r')
hold on
plot(xx,xbc1,'b','linewidth',1)  %%%%% 最终数据
hold on
plot(xx,xb1,'k')
% ylim([0 1800]);
% xlim([300 1860]);

 airPLS函数：

function [Xc,Z]= airPLS(X,lambda,order,wep,p,itermax)if nargin < 6itermax=20;if nargin < 5p=0.05;if nargin < 4wep=0.1;if nargin < 3order=2;if nargin < 2lambda=10e7;if nargin < 1error('airPLS:NotEnoughInputs','Not enough input arguments. See airPLS.');end    end  end  endend
end[m,n]=size(X);
wi = [1:ceil(n*wep) floor(n-n*wep):n];
D = diff(speye(n), order);
DD = lambda*D'*D;
for i=1:mw=ones(n,1);x=X(i,:);for j=1:itermaxW=spdiags(w, 0, n, n);C = chol(W + DD);z = (C\\(C'\\(w .* x')))';d = x-z;dssn= abs(sum(d(d<0)));if(dssn<0.001*sum(abs(x))) break;endw(d>=0) = 0;w(wi)   = p;w(d<0)  = j*exp(abs(d(d<0))/dssn);endZ(i,:)=z;
end
Xc=X-Z;

（2）以乙醇的拉曼光谱数据处理为例：

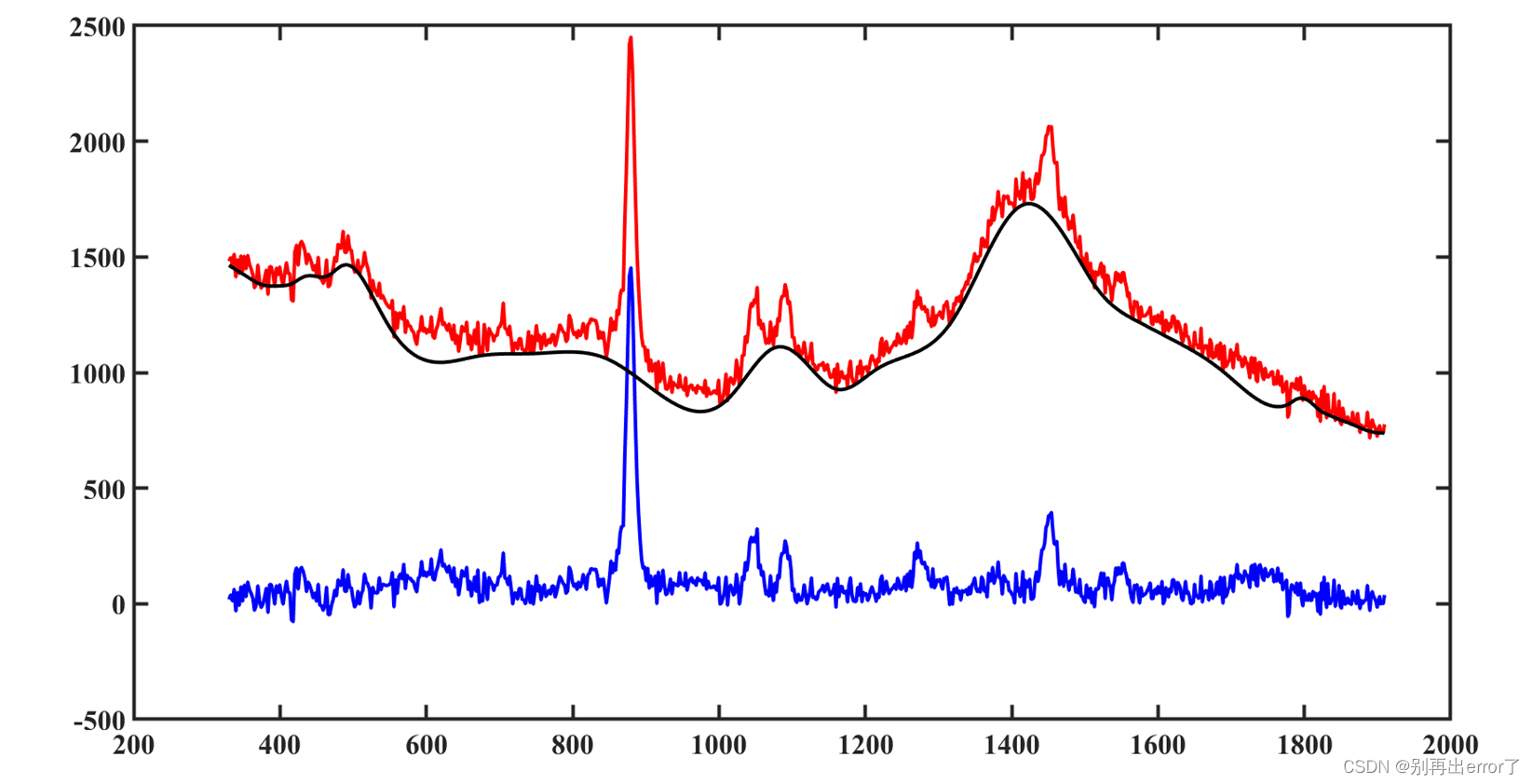
        红色曲线为原始数据，黑色曲线为基线拟合数据，蓝色曲线为扣除基线后的拉曼数据。

参考文献：

[1] Z. M. Zhang, S. Chen, Y. Z. Liang, et al. An intelligent background-correction algorithm for highly fluorescent samples in Raman spectroscopy[J]. Journal of Raman Spectroscopy, 2009, 41(6): 659-669.

网络标签：

相关问题