考察重点

• 算法复杂度: 空间 , 时间
• 算法思维: 贪心 , 二分 , 动态规划
• 常见数据结构

什么是复杂度

• 程序执行时需要的计算量和内存空间（和代码是否简洁无关）
• 复杂度是数量级（方便记忆、推广），不是具体的数字
• 一般针对一个具体的算法，而非一个完整的系统

时间复杂度-程序执行时需要的计算量(CPU)

• O(1）一次就够（数量级）
• O(logn) 数据量的对数（数量级）
• O(n）和传输的数据量一样（数量级）
• O(n * logn) 数据量*数据量的对数（数量级）
• O(n^2) 数据量的平方（数量级）

代码演示

// 复杂度: O(1)
function fn(obj: object) {return obj.a + obj.b + obj.c // 计算量4-5
}// 复杂度: O(n)
function fn(arr = []) {for (var i = 0; i < arr.length; i++) {console.log(arr[i]);}
}// 复杂度: O(n^2)
function fn(arr = []) {for (var i = 0; i < arr.length; i++) {for (var j = 0; j < arr.length; j++) {console.log(arr[j]);}}
}
// 复杂度: O(logn) 二分
// 复杂度: O(n*logn) for循环嵌套 二分 

空间复杂度 -程序执行时需要的内存空间

代码演示

// 空间复杂度 O(1)
function fn(arr = []) {const a = arr[0]const b = arr[1]
}
// 空间复杂度 O(n)
function fn(arr = []) {const arr2 = []for (let i = 0; i < arr.length; i++) {arr2[i] = arr[i]}// ...
}

程序员必须掌握算法复杂度

• 如果你没有复杂度的概念和敏感度，写程序是非常危险的
• 例如，代码功能测试正常，但数量大了，程序就会崩溃
• 对于前端开发，尤其是时间复杂度

重点

• 算法复杂度是学习算法的基础，非常重要
• 复杂度是数量级，用O(.）表示，内部是一个函数表达式
• 前端开发：重时间，轻空间

算法题精析

1. 将一个数组旋转k步

• 输入一个数组 [1,2,3, 4,5,6,7]
• k=3，即旋转3步
• 输出 [5,6,7,1,2,3,4]

思路1：把末尾的元素挨个 pop，然后 unshift 到数组前面
思路2：把数组拆分，最后 concat 拼接到一起

/* @description: 旋转数组k步 使用 pop 和 unshift (时间复杂度 O(n^2），空间复杂度 O(1))* @param {number} arr 旋转目标数组* @param {number} k 步数* @return {*}*/
function rotate1(arr: number[], k: number): number[] {const length = arr.length;if (!k || length == 0) return arr;const step = Math.abs(k % length)// O(n^2）for (let i = 0; i < step; i++) {const n = arr.pop();if (n) {arr.unshift(n) // 数组是一个有序结构 unshift 操作会非常慢!!! O(n）}}return arr;
}
/* @description: 旋转数组k步 使用 concat (时间复杂度O(1），空间复杂度O(n）推荐)* @param {number} arr 旋转目标数组* @param {number} k 步数* @return {*}*/
function rotate2(arr: number[], k: number): number[] {const length = arr.length;if (!k || length == 0) return arr;const step = Math.abs(k % length)const part1 = arr.slice(-step)const part2 = arr.slice(0, length - step)const part3 = part1.concat(part2)return part3;
}// 时间复杂度 性能测试
const arr = [];for (let i = 0; i < 10 * 10000; i++) {arr.push(i);}console.time('rotate1');rotate1(arr, 9 * 10000);console.timeEnd('rotate1');// rotate1: 928.369873046875 ms O(n^2）const arr2 = [];for (let i = 0; i < 10 * 10000; i++) {arr2.push(i);}console.time('rotate2');rotate2(arr2, 9 * 10000);console.timeEnd('rotate2');// rotate2: 0.567138671875 ms O(1）

划重点

• 注意算法时间复杂度 （前端重时间，轻空间）
• 识破内置 API 的时间复杂度（如 unshift)
• 单元测试，考虑参数非法情况，提升代码健壮性

2. 判断字符串是否括号匹配

• 一个字符串＄可能包含{}（）[]三种括号
• 判断S 是否是括号匹配的
• 如(a{blc) 匹配，而{a(b或 {a(b}c） 就不匹配

思路

• 遇到左括号{（[就压栈
• 遇到右括号}）]就判断栈顶，匹配则出栈

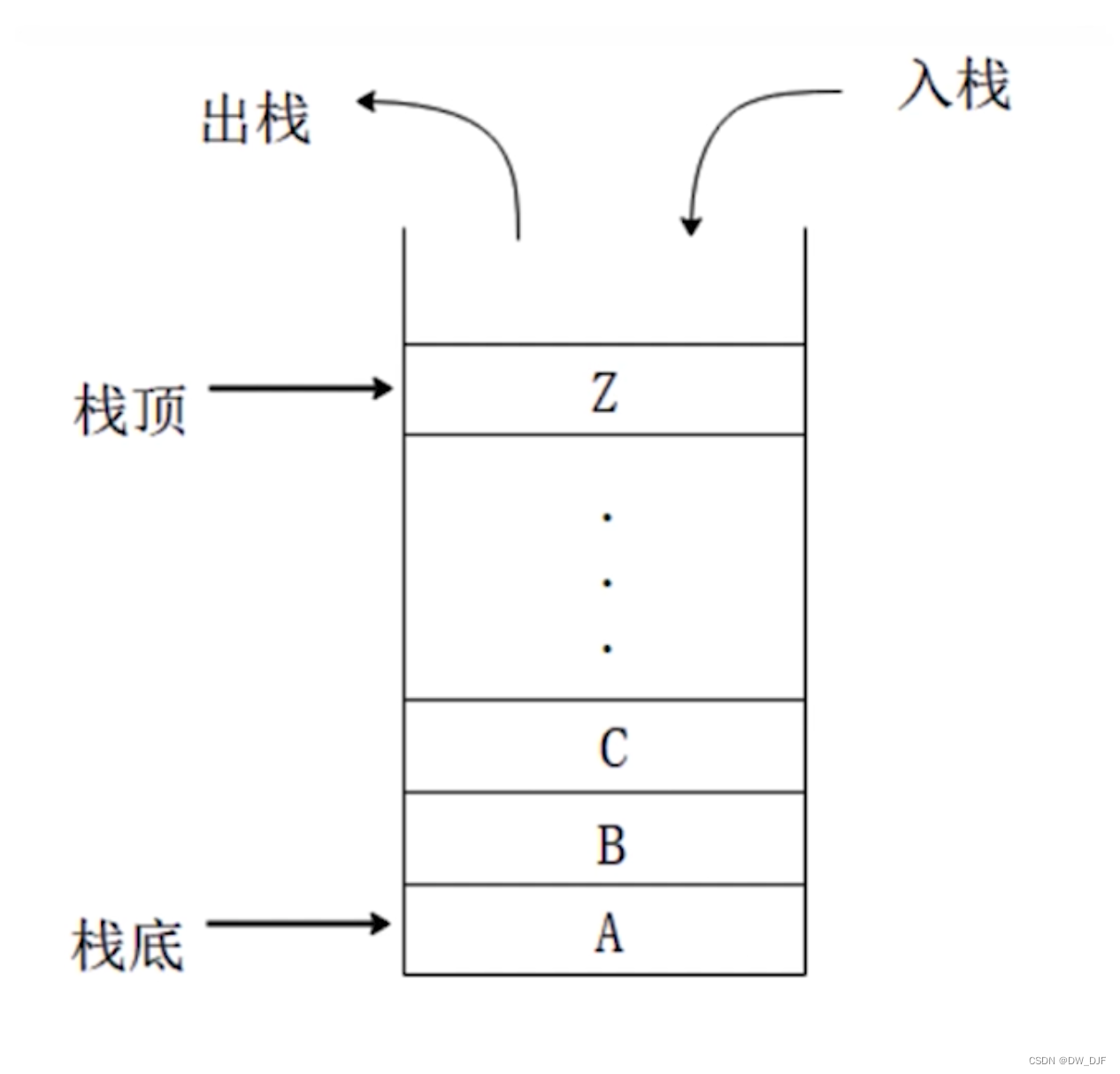
栈

• 先进后出
• API: push pop length
• 相关的：队列，堆
  

逻辑结构 vs 物理结构

• 栈 vs 数组
• 栈，逻辑结构。理论模型，不管如何实现，不受任何语言的限制
• 数组，物理结构。真实的功能实现，受限于编程语言

/* @description: 判断左右括号是否匹配 (时间复杂度 O(n),空间复杂度 O(n))* @param {*} left* @param {*} right* @return {*}*/function isMatch(left: string, right: string): boolean {if (left === '{' && right === '}') return true;if (left === '[' && right === ']') return true;if (left === '(' && right === ')') return true;return false;}function matchBracket(str: string): boolean {const length = str.length;if (length == 0) return true;const stack = [];const leftSymbols = '{[(';const rightSymbols = '}])';for (let i = 0; i < length; i++) {const s = str[i];if (leftSymbols.includes(s)) {// 左括号 压栈stack.push(s);} else if (rightSymbols.includes(s)) {// 右括号,判断栈顶(是否出栈)const top = stack[stack.length - 1];if (isMatch(top, s)) {stack.pop();} else {return false;}}}return stack.length === 0;}

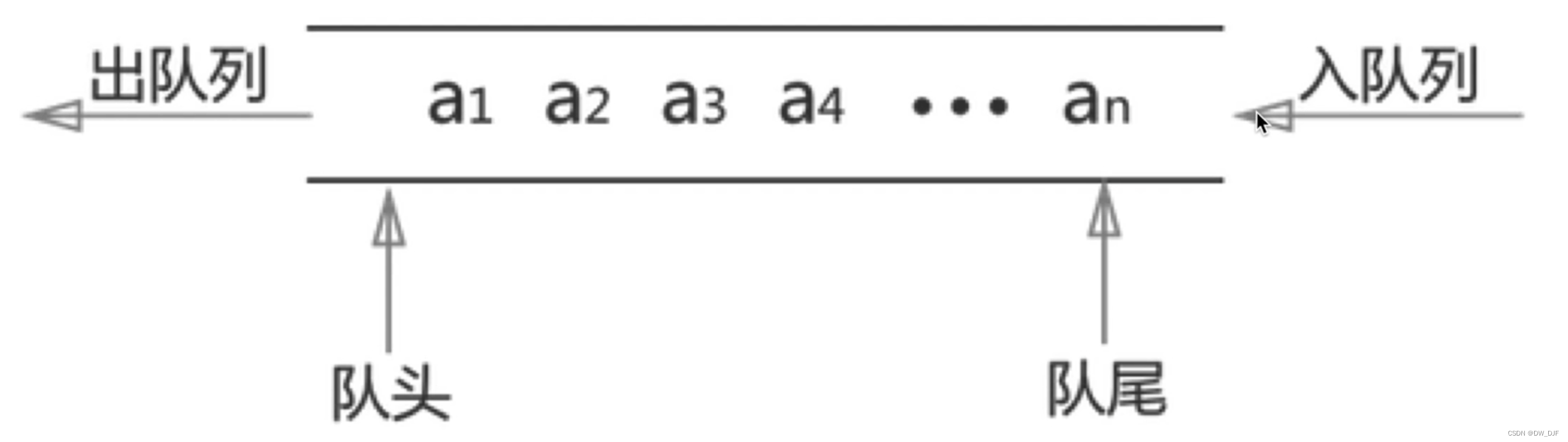
3. 两个栈实现一个队列

• 请用两个栈，实现一个队列(先进先出)
• 功能 add delete length
  

/* @description: 两个栈 一个队列 (空间复杂度O(n))* @return {*}*/class myQueue {private stack1: number[] = [];private stack2: number[] = [];// 时间复杂度 O(1)add(n: number) {this.stack1.push(n);}// 时间复杂度 O(n)delete(): number | null {let res;const stack1 = this.stack1;const stack2 = this.stack2;// 将 stack1 所有元素移动到 stack2 中while (stack1.length > 0) {const n = stack1.pop();if (n != null) {stack2.push(n);}}// stack2 popres = stack2.pop();// 将 stack2 所有元素移动到 stack1 中while (stack2.length > 0) {const n = stack2.pop();if (n != null) {stack1.push(n);}}return res || null;}get length(): number {return this.stack1.length;}}// 功能测试const q = new myQueue();q.add(100);q.add(200);q.add(300);console.info(q.length); // 3console.info(q.delete()); // 100console.info(q.length); // 2

4. 定义一个JS函数，反转单向链表

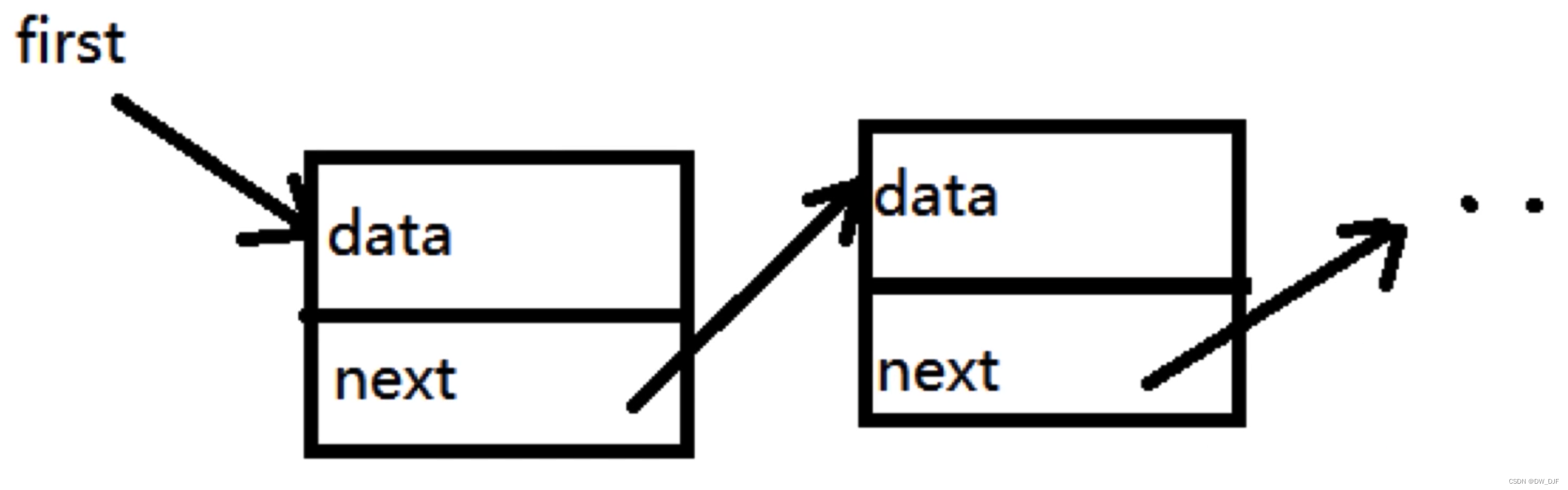
链表: 链表是一种物理结构（非逻辑结构），类似于数组; 数组需要一段连续的内存区间，而链表是零散的; 链表节点的数据结构{value, next?, prev?}

链表 vs 数组

• 都是有序结构
• 链表：查询慢 O(n)，新增和删除快 O(1)
• 数组：查询快 O(1)，新增和删除慢 O(n)

解题思路

• 反转，即节点 next 指向前一个节点
• 但这很容易造成 nextNode 的丢失
• 需要三个指针 prevNode curNode nextNode

  interface ILinkListNode {value: number;next?: ILinkListNode;}/* @description: 根据数组创建单项链表* @param {*} arr* @return {*}*/function createLinkList(arr: number[]): ILinkListNode {const length = arr.length;if (length == 0) throw new Error('arr is empty');// arr: [100,200,300]// {value: 300}// {value: 200,next: {value: 300}}// {value: 100,next: {value: 200,next: {value: 300}}}let curNode: ILinkListNode = {value: arr[arr.length - 1],};if (length == 1) return curNode; for (let i = arr.length - 2; i >= 0; i--) {curNode = {value: arr[i],next: curNode,};}return curNode;}/* @description: 反转单向链表,并返回反转之后的 headNode* @param {*} listNode headNode* @return {*}*/function reverseLinkList(listNode: ILinkListNode): ILinkListNode {// 定义三个指针let prevNode: ILinkListNode | undefined = undefined;let curNode: ILinkListNode | undefined = undefined;let nextNode: ILinkListNode | undefined = listNode;// 以 nextNode 为主, 遍历链表while (nextNode) {// 第一个元素,删掉nextNode,防止循环引用if (curNode && !prevNode) {// @ts-ignoredelete curNode.next;}// 反转指针if (curNode && prevNode) {curNode.next = prevNode;}// 整体向后移动指针prevNode = curNode;curNode = nextNode;nextNode = nextNode?.next;}// 当nextNode为空时,此时curNode尚未设置nextcurNode!.next = prevNode;return curNode!;}// 功能测试const arr = [100, 200, 300, 400, 500];const list = createLinkList(arr);console.log(list);const list1 = reverseLinkList(list);console.log(list1);

链表和数组哪个实现队列更快-分析解题思路

• 数组是连续存储，push 很快，shift 很慢
• 链表是非连续存储，add 和 delete 都很快（但查找很慢）
• 结论：链表实现队列更快

链表实现队列

• 单向链表，但要同时记录 head 和 tail
• 要从 tail 入队，从 head 出队，否则出队时 tail 不好定位
• length 要实时记录，不可遍历链表获取