循环题目讲解

输出倒三角形
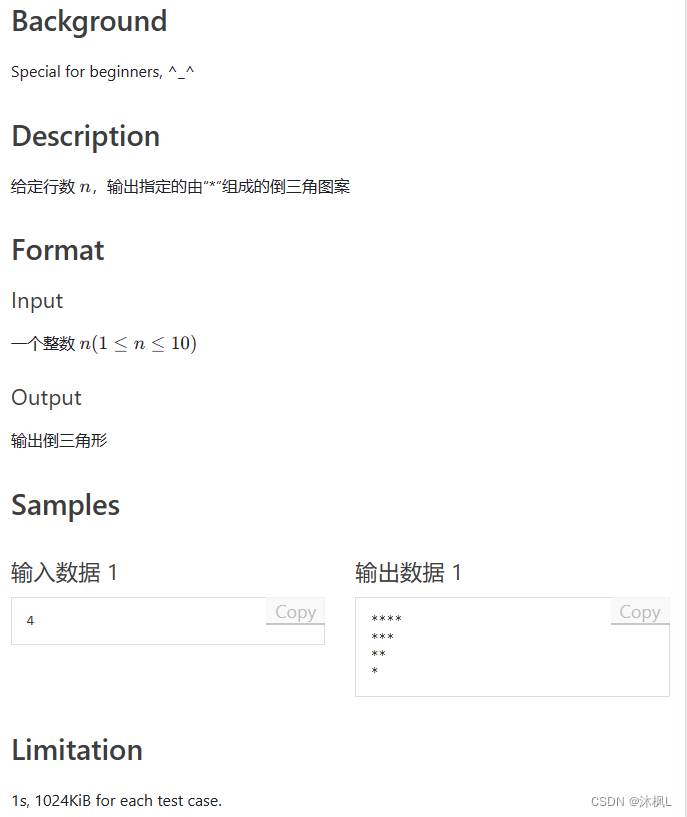
由题目可以看出,输出共有 nnn 行,第 111 行输出 nnn 个字符,第 222 行输出 n−1n-1n−1 个字符,…\\dots…,第 nnn 行输出 111 个字符。
对于这种 n,n−1,n−2,…,1n,n-1,n-2,\\dots,1n,n−1,n−2,…,1 的序列,我们可以有 222 种方法产生:
- 循环变量
i从n开始,每次--i,直到1为止;
| i | n | n-1 | n-2 | n-3 | … | 2 | 1 |
|---|---|---|---|---|---|---|---|
| x | n | n-1 | n-2 | n-3 | … | 2 | 1 |
- 通过观察可以发现,第
i个数x一定满足x=n-i+1。
| i | 1 | 2 | 3 | 4 | … | n-1 | n |
|---|---|---|---|---|---|---|---|
| x | n | n-1 | n-2 | n-3 | … | 2 | 1 |
| n-i+1 | n-1+1 | n-2+1 | n-3+1 | n-4+1 | … | n-(n-1)+1 | n-n+1 |
打印图形
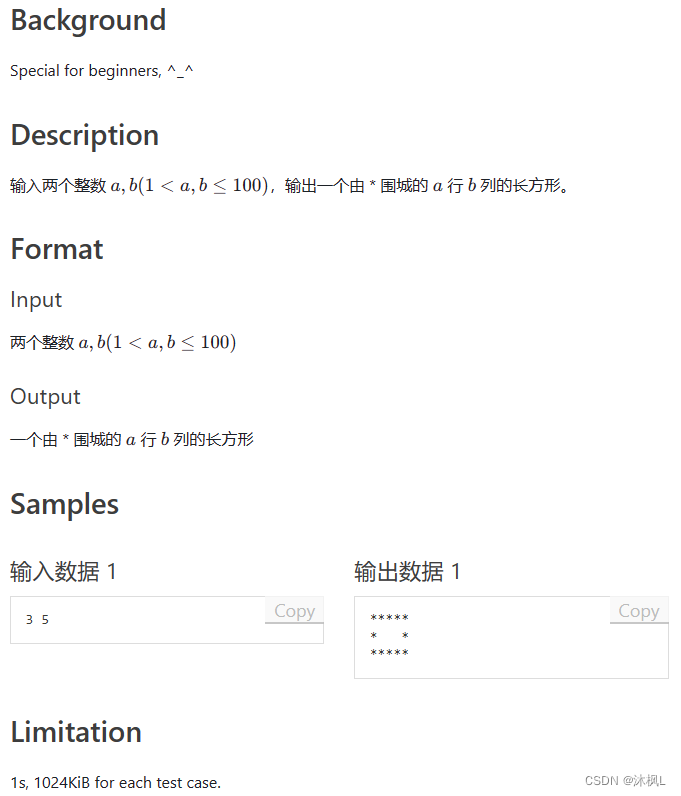
两种思路:
- 把图形分成 333 部分,第 111 行,中间 n−2n-2n−2 行,第 nnn 行,注意中间每行两个星花间的空格都需要实际输出,否则两个星花是紧挨在一起的;
- 统一看成一个整体,用两层循环,当每行输出的位置既不是第 111 列,也不是第 nnn 列时,以当前是否是第 111 行或者第 nnn 行为判断标准,决定在此是输出星花还是空格。
