上一章的 RNN 存在环路，可以记忆过去的信息，其结构非常简单，易于实现。不过，遗憾的是，这个 RNN 的效果并不好。原因在于，许多情况下它都无法很好地学习到时序数据的长期依赖关系。

现在，上一章的简单 RNN 经常被名为 LSTM 或 GRU 的层所代替。实际上，当我们说 RNN 时，更多的是指 LSTM 层，而不是上一章的 RNN。 顺便说一句，当需要明确指上一章的 RNN 时，我们会说“简单 RNN”或 “Elman”。

LSTM 和 GRU 中增加了一种名为 “门” 的结构。基于这个门，可以学习到时序数据的长期依赖关系。

6.1 RNN的问题

RNN 之所以不擅长学习时序数据的长期依赖关系，是因 为 BPTT 会发生梯度消失和梯度爆炸的问题。

6.1.1 RNN的复习

RNN 层存在环路。如果展开它的循环，它将变成一个在水平方向上延伸的网络，如图 6-1 所示。

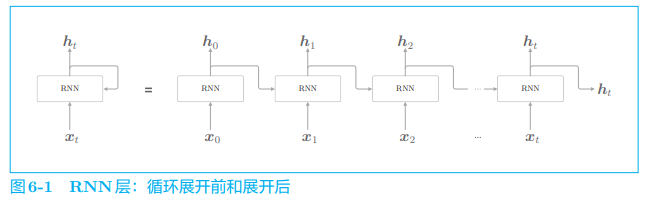
在图 6-1 中，当输入时序数据 xtx_txt​ 时，RNN 层输出 hth_tht​。这个 hth_tht​ 也称为 RNN 层的隐藏状态，它记录过去的信息。

RNN 的特点在于使用了上一时刻的隐藏状态，由此，RNN 可以继承过去的信息。顺便说一下，如果用计算图来表示此时 RNN 层进行的处理，则有图 6-2。

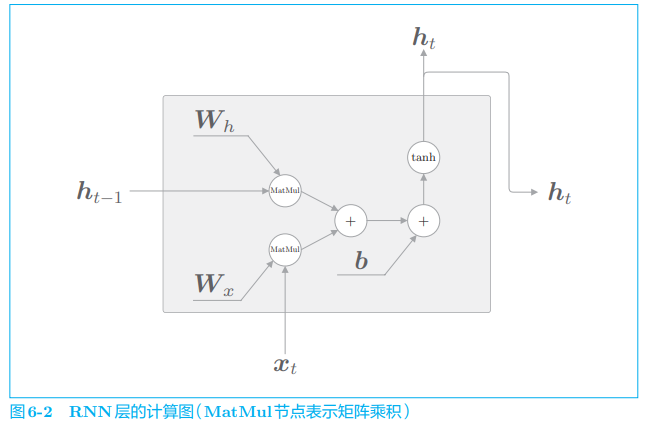
如图 6-2 所示，RNN 层的正向传播进行的计算由矩阵乘积、矩阵加法和基于激活函数 tanh 的变换构成，这就是我们上一章看到的 RNN 层。下 面，我们看一下这个 RNN 层存在的问题（关于长期记忆的问题）。

6.1.2 梯度消失和梯度爆炸

语言模型的任务是根据已经出现的单词预测下一个将要出现的单词。上一章我们实现了基于 RNN 的语言模型 RNNLM，这里借着探讨 RNNLM 问题的机会，我们再来考虑一下图 6-3 所示的任务。

插入图6-3

如前所述，填入 “?” 中的单词应该是 Tom。要正确回答这个问题， RNNLM 需要记住 “Tom 在房间看电视，Mary 进了房间” 这些信息。这些信息必须被编码并保存在 RNN 层的隐藏状态中。

现在让我们站在 RNNLM 进行学习的角度来考虑上述问题。在正确解标签为 Tom 时，RNNLM 中的梯度是如何传播的呢？这里我们使用 BPTT 进行学习，因此梯度将从正确解标签 Tom 出现的地方向过去的方向传播，如图 6-4 所示。

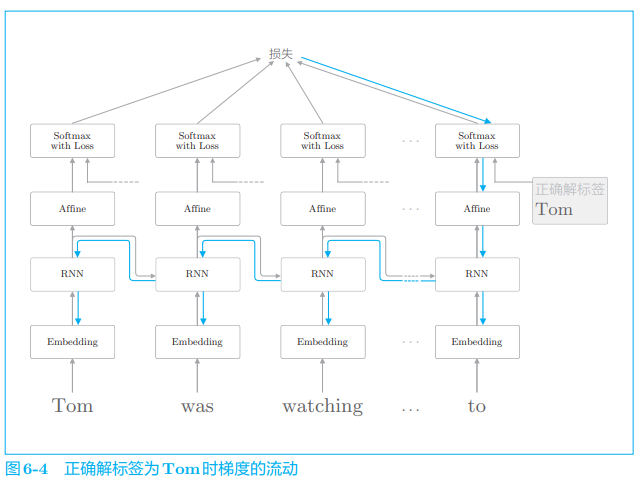
在学习正确解标签 Tom 时，重要的是 RNN 层的存在。RNN 层通过向过去传递 “有意义的梯度”，能够学习时间方向上的依赖关系。此时梯度（理论上）包含了那些应该学到的有意义的信息，通过将这些信息向过去传递，RNN 层学习长期的依赖关系。但是，如果这个梯度在中途变弱（甚至没有包含任何信息），则权重参数将不会被更新。也就是说，RNN 层无法学习长期的依赖关系。不幸的是，随着时间的回溯，这个简单 RNN 未能避免梯度变小（梯度消失）或者梯度变大（梯度爆炸）的命运。

6.1.3 梯度消失和梯度爆炸的原因

现在，我们深挖一下 RNN 层中梯度消失（或者梯度爆炸）的起因。如图 6-5 所示，这里仅关注 RNN 层在时间方向上的梯度传播。

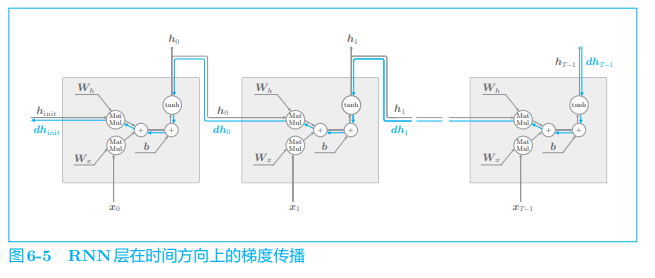
如图 6-5 所示， 这里考虑长度为 $T$ 的时序数据，关注从第 $T$ 个正确解标签传递出的梯度如何变化。就上面的问题来说，这相当于第 $T$ 个正确解标签是 Tom 的情形。此时，关注时间方向上的梯度，可知反向传播的梯度流经 tanh、“+” 和 MatMul（矩阵乘积）运算。

“+” 的反向传播将上游传来的梯度原样传给下游，因此梯度的值不变。 那么，剩下的 tanh 和 MatMul 运算会怎样变化呢？我们先来看一下 tanh。

附录 A 中会详细说明。当 $y=tanh(x)$ 时，它的导数是 dydx=1−y2\\frac{dy}{dx} = 1 − y^2dxdy​=1−y2 。 此时，将 $y=tanh(x)$ 的值及其导数的值分别画在图上，如图 6-6 所示。

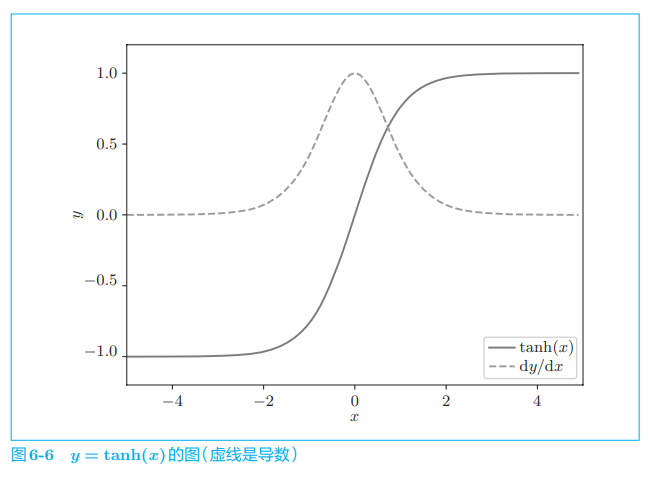
图 6-6 中的虚线是 $y=tanh(x)$ 的导数。从图中可以看出，它的值小于 $1.0$，并且随着 $x$ 远离 $0$，它的值在变小。这意味着，当反向传播的梯度经过 $tanh$ 节点时，它的值会越来越小。因此，如果经过 $tanh$ 函数 $T$ 次，则梯度也会减小 $T$ 次。

RNN 层的激活函数一般使用 tanh 函数，但是如果改为 ReLU 函数， 则有希望抑制梯度消失的问题（当 ReLU 的输入为 $x$ 时，它的输出是 $max(0,x)$）。这是因为，在 ReLU 的情况下，当 $x$ 大于 $0$ 时，反向传播将上游的梯度原样传递到下游，梯度不会 “退化”。

接下来，我们关注图 6-5 中的 MatMul（矩阵乘积）节点。简单起见，这里我们忽略图 6-5 中的 tanh 节点。如此一来，如图 6-7 所示，RNN 层的反向传播的梯度就仅取决于 MatMul 运算。

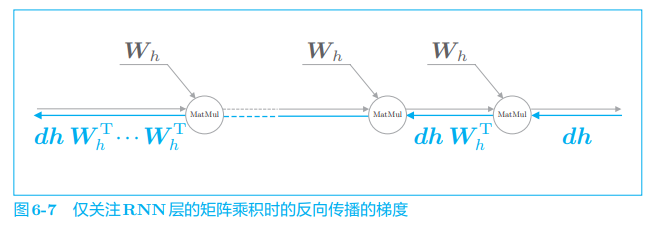
在图 6-7 中，假定从上游传来梯度 $dh$，此时 MatMul 节点的反向传播通过矩阵乘积 dhWhTdhW_h^TdhWhT​ 计算梯度。之后，根据时序数据的时间步长，将这个计算重复相应次数。这里需要注意的是，每一次矩阵乘积计算都使用相同的权重 WhW_hWh​。

这里通过下面的代码，来观察梯度大小的变化：

import numpy as np
import matplotlib.pyplot as pltN = 2 # mini-batch的大小
H = 3 # 隐藏状态向量的维数
T = 20 # 时序数据的长度dh = np.ones((N, H))
np.random.seed(3) # 为了复现，固定随机数种子
Wh = np.random.randn(H, H)norm_list = []
for t in range(T):dh = np.dot(dh, Wh.T)norm = np.sqrt(np.sum(dh2)) / Nnorm_list.append(norm)

这里用 np.ones() 初始化 $dh$（np.ones() 是所有元素均为 1 的矩阵）。然后，根据反向传播的 MatMul 节点的数量更新 $dh$ 相应次数，并将各步的 $dh$ 的大小（范数）添加到 norm_list 中。这里，$dh$ 的大小是 mini-batch（$N$ 笔） 中的平均 “L2 范数”。L2 范数对所有元素的平方和求平方根。

将上述代码的执行结果（norm_list）画在图上，如图 6-8 所示。

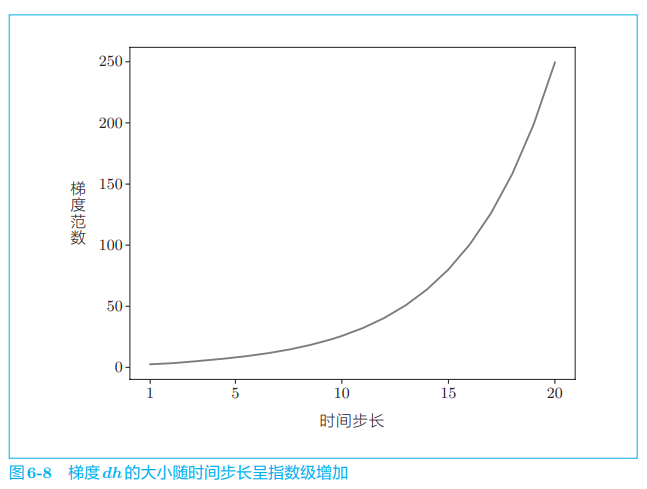
如图 6-8 所示，可知梯度的大小随时间步长呈指数级增加，这就是梯度爆炸（exploding gradients）。如果发生梯度爆炸，最终就会导致溢出，出现 NaN（Not a Number，非数值）之类的值。如此一来，神经网络的学习将无法正确运行。

现在做第 2 个实验，将 WhW_hWh​ 的初始值改为下面的值。

# Wh = np.random.randn(H, H) # before
Wh = np.random.randn(H, H) * 0.5 # after

使用这个初始值，进行与上面相同的实验，结果如图 6-9 所示。

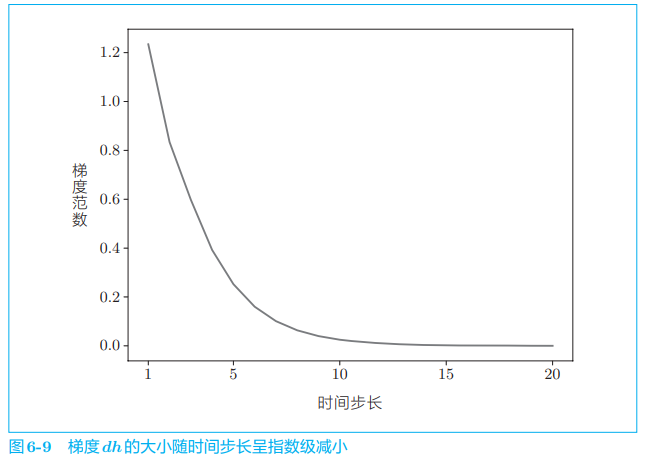
从图 6-9 中可以看出，这次梯度呈指数级减小，这就是梯度消失 （vanishing gradients）。如果发生梯度消失，梯度将迅速变小。一旦梯度变小，权重梯度不能被更新，模型就会无法学习长期的依赖关系。

在这里进行的实验中，梯度的大小或者呈指数级增加，或者呈指数级减小。为什么会出现这样的指数级变化呢？因为矩阵 WhW_hWh​ 被反复乘了 $T$ 次。如 果 WhW_hWh​ 是标量，则问题将很简单：当 WhW_hWh​ 大于 $1$ 时，梯度呈指数级增加；当 WhW_hWh​ 小于 $1$ 时，梯度呈指数级减小。

那么，如果 WhW_hWh​ 不是标量，而是矩阵呢？此时，矩阵的奇异值将成为指标。简单而言，矩阵的奇异值表示数据的离散程度。根据这个奇异值（更准确地说是多个奇异值中的最大值）是否大于 1，可以预测梯度大小的变化。

如果奇异值的最大值大于 $1$，则可以预测梯度很有可能会呈指数级增加；而如果奇异值的最大值小于 $1$，则可以判断梯度会呈指数级减小。但是，并不是说奇异值比 $1$ 大就一定会出现梯度爆炸。 也就是说，这是必要条件，并非充分条件。

6.1.4 梯度爆炸的对策

至此，我们探讨了 RNN 的梯度爆炸和梯度消失问题，现在我们继续讨论解决方案。首先来看一下梯度爆炸。

解决梯度爆炸有既定的方法，称为梯度裁剪（gradients clipping）。这 是一个非常简单的方法，它的伪代码如下所示：
if∣∣g^∣∣≥threshold:g^=threshold∣∣g^∣∣g^\\begin{align} if \\ \\ ||\\hat{g}|| &\\ge threshold: \\\\ \\hat{g} &= \\frac{threshold}{||\\hat{g}||} \\hat{g} \\end{align} if  ∣∣g^​∣∣g^​​≥threshold:=∣∣g^​∣∣threshold​g^​​​
这里假设可以将神经网络用到的所有参数的梯度整合成一个，并用符号 g^\\hat{g}g^​ 表 示。另外，将阈值设置为 $threshold$。此时，如果梯度的 L2 范数 g^\\hat{g}g^​ 大于或等于阈值，就按上述方法修正梯度，这就是梯度裁剪。如你所见，虽然这个方法很简单，但是在许多情况下效果都不错。

g^\\hat{g}g^​ 整合了神经网络中用到的所有参数的梯度。比如，当某个模型 有 W1W_1W1​ 和 W2W_2W2​ 两个参数时，$hatg$ 就是这两个参数对应的梯度 dW1dW_1dW1​ 和 dW2dW_2dW2​ 的组合。

代码实现：见书

6.2 梯度消失和LSTM

在 RNN 的学习中，梯度消失也是一个大问题。为了解决这个问题，需要从根本上改变 RNN 层的结构，这里本章的主题 Gated RNN 就要登场了。

人们已经提出了诸多 Gated RNN 框架（网络结构），其中具有代表性的有 LSTM 和 GRU。本节我们将关注 LSTM，仔细研究它的结构，并阐明为何它不会（难以）引起梯度消失。另外，附录 C 中会对 GRU 进行说明。

6.2.1 LSTM的接口

接下来，我们仔细看一下 LSTM 层。在此之前，为了将来方便，我们在计算图中引入 “简略图示法”。如图 6-10 所示，这种图示法将矩阵计算等整理为一个长方形节点。

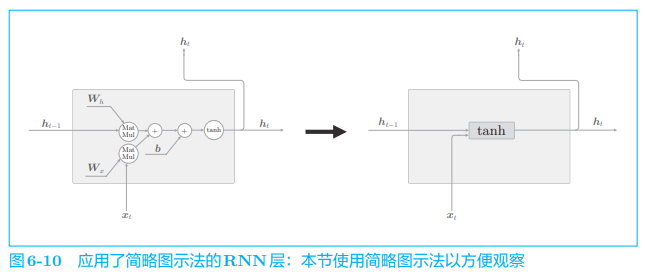
如图 6-10 所示，这里将 tanh(ht−1Wh+xtWx+b)tanh(h_{t−1}W_h + x_tW_x + b)tanh(ht−1​Wh​+xt​Wx​+b) 这个计算表示为 一个长方形节点 tanh（ht−1h_{t−1}ht−1​ 和 xtx_txt​ 是行向量），这个长方形节点中包含了矩阵乘积、偏置的和以及基于 tanh 函数的变换。

首先，我们来比较一下 LSTM 与 RNN 的接口（输入和输出）（图 6-11）。

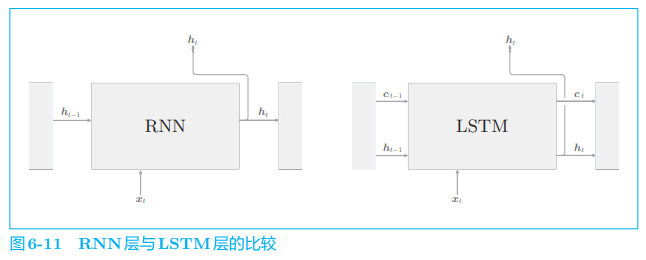
如图 6-11 所示，LSTM 与 RNN 的接口的不同之处在于，LSTM 还有路径 $c$。这个 $c$ 称为记忆单元（或者简称为“单元”），相当于 LSTM 专用的记忆部门。

记忆单元的特点是，仅在 LSTM 层内部接收和传递数据。也就是说，记忆单元在 LSTM 层内部结束工作，不向其他层输出。而 LSTM 的隐藏状态 $h$ 和 RNN 层相同，会被（向上）输出到其他层。

从接收 LSTM 的输出的一侧来看，LSTM 的输出仅有隐藏状态向量 $h$。记忆单元 $c$ 对外部不可见，我们甚至不用考虑它的存在。

6.2.2 LSTM层的结构

如前所述，LSTM 有记忆单元 ctc_tct​。这个 ctc_tct​ 存储了时刻 $t$ 时 LSTM 的记忆，可以认为其中保存了从过去到时刻 $t$ 的所有必要信息（或者以此为目的进行了学习）。然后，基于这个充满必要信息的记忆，向外部的层（和下一 时刻的 LSTM）输出隐藏状态 hth_tht​。如图 6-12 所示，LSTM 输出经 tanh 函数变换后的记忆单元。

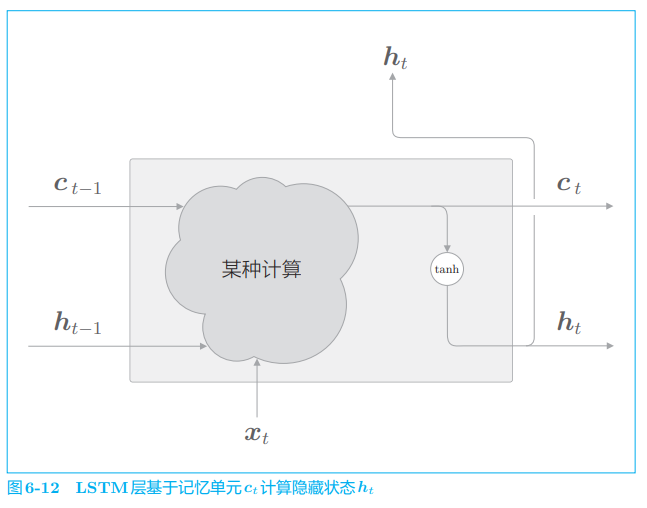
如图 6-12 所示，当前的记忆单元 ctc_tct​ 是基于 3 个输入 ct−1c_{t−1}ct−1​、ht−1h_{t−1}ht−1​ 和 xtx_txt​，经过 “某种计算”（后述）算出来的。这里的重点是隐藏状态 hth_tht​ 要使用更新后的 ctc_tct​ 来计算。另外，这个计算是 ht=tanh(ct)h_t = tanh(c_t)ht​=tanh(ct​)，表示对 ctc_tct​ 的各个元素应用 tanh 函数。

到目前为止，记忆单元 ctc_tct​ 和隐藏状态 hth_tht​ 的关系只是按元素应用 tanh 函数。这意味着，记忆单元 ctc_tct​ 和隐藏状态 hth_tht​ 的元素个数相同。如果记忆单元 ctc_tct​ 的元素个数是 100，则隐藏状态 hth_tht​ 的元素个数也是 100。

6.2.3 输出门

在刚才的说明中，隐藏状态 hth_tht​ 对记忆单元 ctc_tct​ 仅仅应用了 tanh 函数。这里考虑对 tanh(ctc_tct​) 施加门。换句话说，针对 tanh(ctc_tct​) 的各个元素，调整它们作为下一时刻的隐藏状态的重要程度。由于这个门管理下一个隐藏状态 hth_tht​ 的输出，所以称为输出门（output gate）。

输出门的开合程度（流出比例）根据输入 xtx_txt​ 和上一个状态 ht−1h_{t−1}ht−1​ 求出。此时进行的计算如下式所示。这里在使用的权重参数和偏置的上 标上添加了 output 的首字母 $o$。之后，我们也将使用上标表示门。另外，sigmoid 函数用 $\sigma ()$ 表示。
o=σ(xtWx(o)+ht−1Wh(o)+b(o))o = \\sigma(x_t W_x^{(o)} + h_{t-1} W_h^{(o)} + b^{(o)}) o=σ(xt​Wx(o)​+ht−1​Wh(o)​+b(o))
如式 (6.1) 所示，输入 xtx_txt​ 有权重 Wx(o)W_x^{(o)}Wx(o)​，上一时刻的状态 ht−1h_{t−1}ht−1​ 有权重 Wh(o)W_h^{(o)}Wh(o)​（xtx_txt​ 和 ht−1h_{t−1}ht−1​ 是行向量）。将它们的矩阵乘积和偏置 $b(o)$ 之和传给 sigmoid 函数，结果就是输出门的输出 $o$。最后，将这个 $o$ 和 tanh(ctc_tct​) 的对应元素的乘积作为 hth_tht​ 输出。将这些计算绘制成计算图，结果如图 6-15 所示。

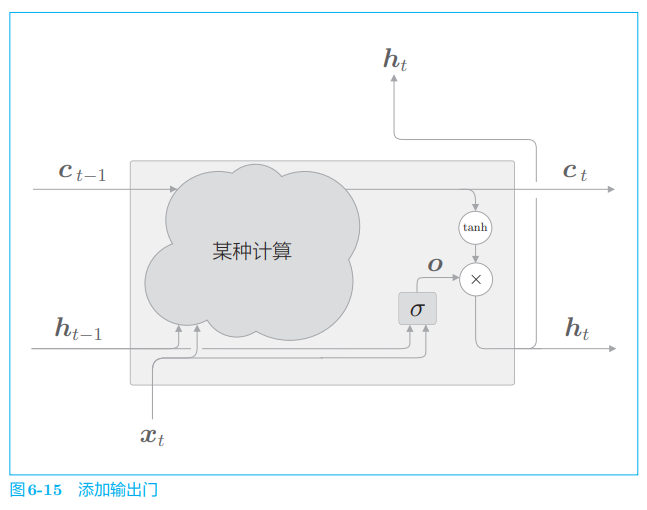
在图 6-15 中，将输出门进行的上式的计算表示为 $\sigma$。然后，将它的输出表示为 $o$，则 hth_tht​ 可由 $o$ 和 tanh(ctc_tct​) 的乘积计算出来。这里说的 “乘积” 是对应元素的乘积，也称为阿达玛乘积。如果用 $\odot$ 表示阿达玛乘积，则此处的计算如下所示：
ht=o⊙tanh(ct)h_t = o\\odot tanh(c_t) ht​=o⊙tanh(ct​)
以上就是 LSTM 的输出门。

tanh 的输出是 $-1.0\sim 1.0$ 的实数。我们可以认为这个 $-1.0\sim 1.0$ 的数值表示某种被编码的 “信息” 的强弱（程度）。而 sigmoid 函数的输出是 $0.0\sim 1.0$ 的实数，表示数据流出的比例。因此，在大多数情况下，门使用 sigmoid 函数作为激活函数，而包含实质信息的数据则使用 tanh 函数作为激活函数。

6.2.4 遗忘门

只有放下包袱，才能轻装上路。接下来，我们要做的就是明确告诉记忆单元需要 “忘记什么”。这里，我们使用门来实现这一目标。

现在，我们在记忆单元 ct−1c_{t−1}ct−1​ 上添加一个忘记不必要记忆的门，这里称为遗忘门（forget gate）。将遗忘门添加到 LSTM 层，计算图如图6-16 所示。

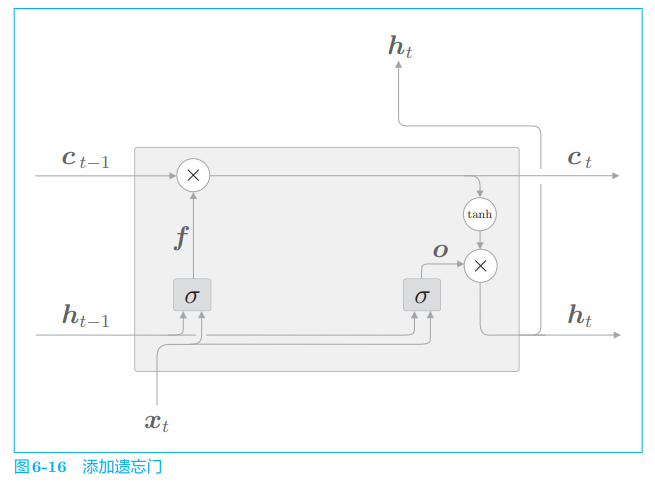
在图 6-16 中，将遗忘门进行的一系列计算表示为 $\sigma$，其中有遗忘门专用的权重参数，此时的计算如下：
f=σ(xtWx(f)+ht−1Wh(f)+b(f))f = \\sigma (x_t W_x^{(f)} + h_{t-1} W_h^{(f)} + b^{(f)}) f=σ(xt​Wx(f)​+ht−1​Wh(f)​+b(f))
遗忘门的输出 $f$ 可以由上式求得。然后，ctc_tct​ 由这个 $f$ 和上一个记忆单元 ct−1c_{t−1}ct−1​ 的对应元素的乘积求得（ct=f⊙ct−1c_t = f \\odot c_{t−1}ct​=f⊙ct−1​）。

6.2.5 新的记忆单元

遗忘门从上一时刻的记忆单元中删除了应该忘记的东西，但是这样一来，记忆单元只会忘记信息。现在我们还想向这个记忆单元添加一些应当记住的新信息，为此我们添加新的 tanh 节点（图 6-17）。

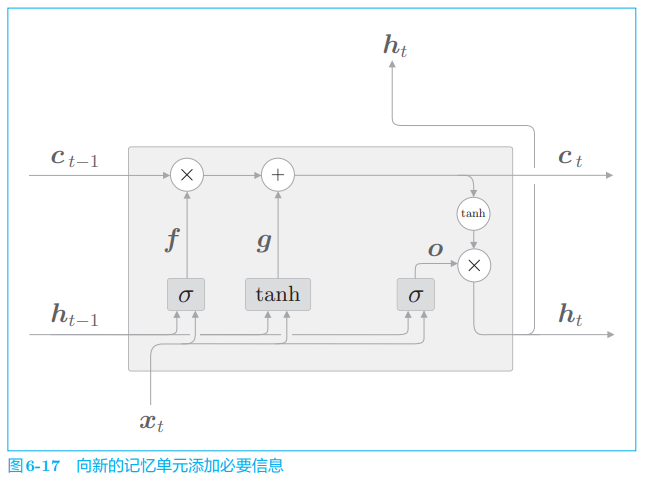
如图 6-17 所示，基于 tanh 节点计算出的结果被加到上一时刻的记忆单元 ct−1c_{t−1}ct−1​ 上。这样一来，新的信息就被添加到了记忆单元中。这个 tanh 节点的作用不是门，而是将新的信息添加到记忆单元中。因此，它不用 sigmoid 函数作为激活函数，而是使用 tanh 函数。tanh 节点进行的计算如下所示：
g=tanh(xtWx(g)+ht−1Wh(g)+b(g))g = tanh(x_t W_x^{(g)} + h_{t-1} W_h^{(g)} + b^{(g)}) g=tanh(xt​Wx(g)​+ht−1​Wh(g)​+b(g))
这里用 $g$ 表示向记忆单元添加的新信息。通过将这个 $g$ 加到上一时刻的 ct−1c_{t−1}ct−1​ 上，从而形成新的记忆。

6.2.6 输入门

最后，我们给图 6-17 的 $g$ 添加门，这里将这个新添加的门称为输入门 （input gate）。添加输入门后，计算图如图 6-18 所示。

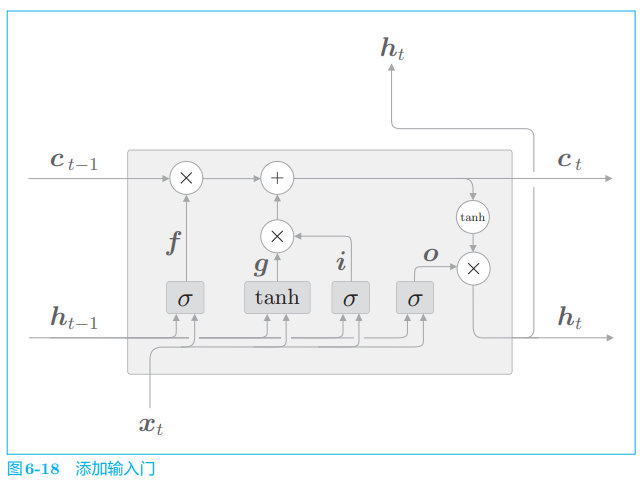
输入门判断新增信息 $g$ 的各个元素的价值有多大。输入门不会不经考虑就添加新信息，而是会对要添加的信息进行取舍。换句话说，输入门会添加加权后的新信息。

在图 6-18 中，用 $\sigma$ 表示输入门，用 $i$ 表示输出，此时进行的计算如下所示：
i=σ(xtWx(i)+ht−1Wh(i)+b(i))i = \\sigma (x_t W_x^{(i)} + h_{t-1} W_h^{(i)} + b^{(i)}) i=σ(xt​Wx(i)​+ht−1​Wh(i)​+b(i))
然后，将 $i$ 和 $g$ 的对应元素的乘积添加到记忆单元中。以上就是对 LSTM 内部处理的说明。

LSTM 有多个 “变体”。这里说明的 LSTM 是最有代表性的 LSTM，也有许多在门的连接方式上稍微不同的其他 LSTM。

6.2.7 LSTM的梯度的流动

上面我们介绍了 LSTM 的结构，那么，为什么它不会引起梯度消失呢？ 其原因可以通过观察记忆单元 $c$ 的反向传播来了解（图 6-19）。

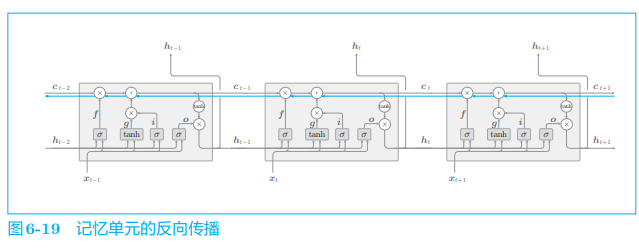
在图 6-19 中，我们仅关注记忆单元，绘制了它的反向传播。此时，记忆单元的反向传播仅流过 “+” 和 “×” 节点。“+” 节点将上游传来的梯度原样流出，所以梯度没有变化（退化）。

而 “×” 节点的计算并不是矩阵乘积，而是对应元素的乘积（阿达玛积）。顺便说一下，在之前的 RNN 的反向传播中，我们使用相同的权重矩阵重复了多次矩阵乘积计算，由此导致了梯度消失（或梯度爆炸）。而这里的 LSTM 的反向传播进行的不是矩阵乘积计算，而是对应元素的乘积计算，而且每次都会基于不同的门值进行对应元素的乘积计算。这就是它不会发生梯度消失（或梯度爆炸）的原因。

图 6-19 的 “×” 节点的计算由遗忘门控制（每次输出不同的门值）。遗忘门认为 “应该忘记” 的记忆单元的元素，其梯度会变小；而遗忘门认为 “不能忘记” 的元素，其梯度在向过去的方向流动时不会退化。因此，可以期待记忆单元的梯度（应该长期记住的信息）能在不发生梯度消失的情况下传播。

从以上讨论可知，LSTM 的记忆单元不会（难以）发生梯度消失。因此， 可以期待记忆单元能够保存（学习）长期的依赖关系。

LSTM是 Long Short-Term Memory（长短期记忆）的缩写，意思是可以长（Long）时间维持短期记忆（Short-Term Memory）。

6.3 LSTM的实现

见书

6.4 使用LSTM的语言模型

见书

6.5 进一步改进RNNLM

6.5.1 LSTM层的多层化

在使用 RNNLM 创建高精度模型时，加深 LSTM 层（叠加多个 LSTM 层）的方法往往很有效。之前我们只用了一个 LSTM 层，通过叠加多个层，可以提高语言模型的精度。例如，在图 6-29 中，RNNLM 使用了两个 LSTM 层。

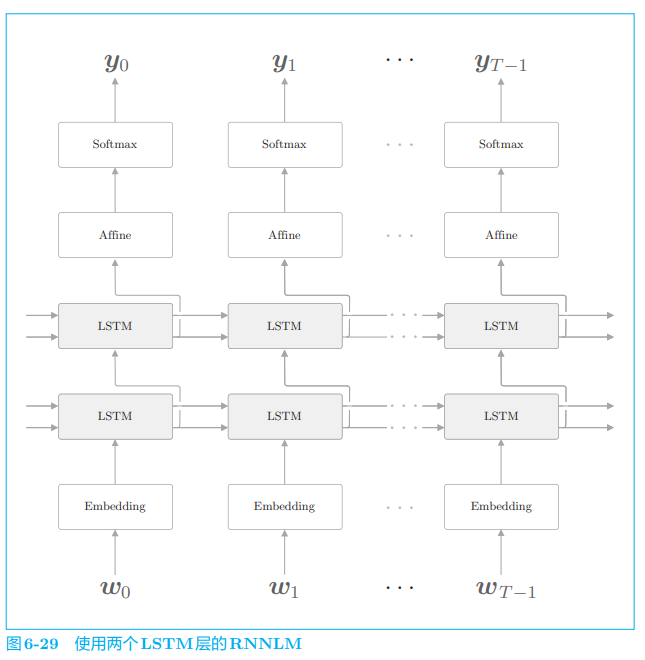
图 6-29 显示了叠加两个 LSTM 层的例子。此时，第一个 LSTM 层的隐藏状态是第二个 LSTM 层的输入。按照同样的方式，我们可以叠加多个 LSTM 层，从而学习更加复杂的模式，这和前馈神经网络时的层加深是一样的。

那么，应该叠加几个层呢？这其实是一个关于超参数的问题。因为层数是超参数，所以需要根据要解决的问题的复杂程度、能给到的训练数据的规模来确定。顺便说一句，在 PTB 数据集上学习语言模型的情况下，当 LSTM 的层数为 2 ～ 4 时，可以获得比较好的结果。

6.5.2 基于Dropout抑制过拟合

通过叠加 LSTM 层，可以期待能够学习到时序数据的复杂依赖关系。 换句话说，通过加深层，可以创建表现力更强的模型，但是这样的模型往往 会发生过拟合（overfitting）。更糟糕的是，RNN 比常规的前馈神经网络更容易发生过拟合，因此 RNN 的过拟合对策非常重要。

过拟合是指过度学习了训练数据的状态，也就是说，过拟合是一种缺乏泛化能力的状态。我们想要的是一个泛化能力强的模型，因此 必须基于训练数据和验证数据的评价差异，判断是否发生了过拟合， 并据此来进行模型的设计。

抑制过拟合已有既定的方法：一是增加训练数据；二是降低模型的复杂度。我们会优先考虑这两个方法。除此之外，对模型复杂度给予惩罚的正则化也很有效。比如，L2 正则化会对过大的权重进行惩罚。

此外，像 Dropout 这样，在训练时随机忽略层的一部分（比如 50%）神经元，也可以被视为一种正则化（图 6-30）。本节我们将仔细研究 Dropout，并将其应用于 RNN。

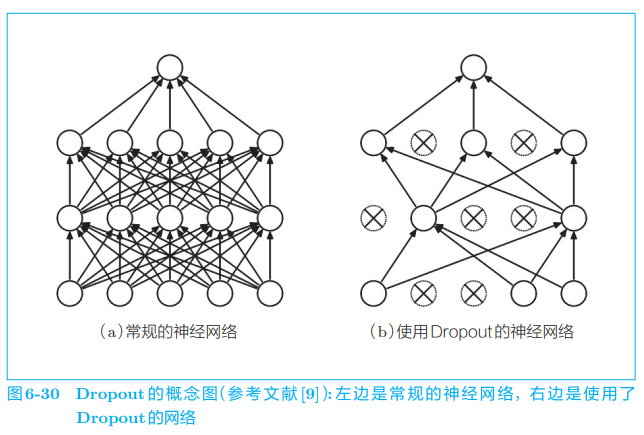
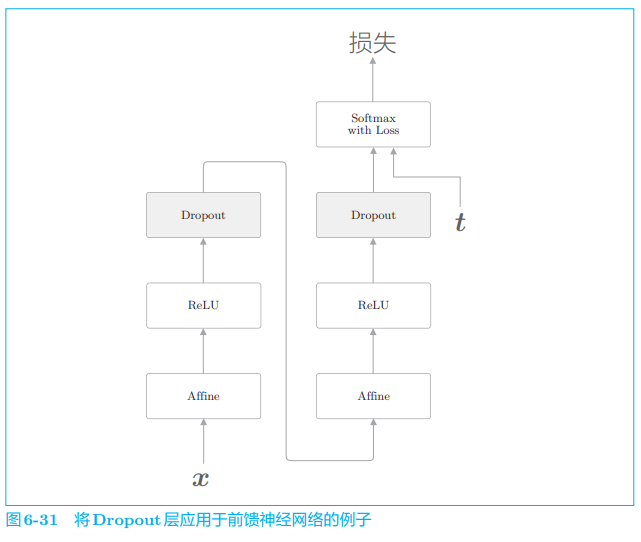
如图 6-30 所示，Dropout 随机选择一部分神经元，然后忽略它们，停止向前传递信号。这种 “随机忽视” 是一种制约，可以提高神经网络的泛化能力。我们在前作《深度学习入门：基于 Python 的理论与实现》中已经实现了 Dropout。如图 6-31 所示，当时我们给出了在激活函数后插入 Dropout 层的示例，并展示了它有助于抑制过拟合。

那么，在使用 RNN 的模型中，应该将 Dropout 层插入哪里呢？首先可以想到的是插入在 LSTM 层的时序方向上，如图 6-32 所示。不过答案是， 这并不是一个好的插入方式。

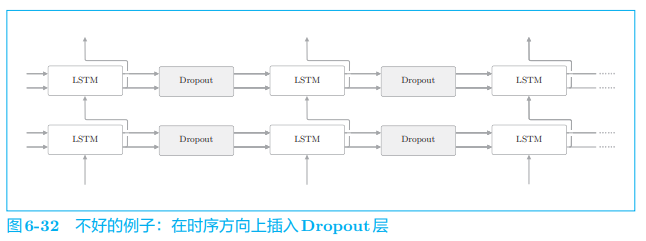
如果在时序方向上插入 Dropout，那么当模型学习时，随着时间的推移，信息会渐渐丢失。也就是说，因 Dropout 产生的噪声会随时间成比例地积累。考虑到噪声的积累，最好不要在时间轴方向上插入 Dropout。因此，如图 6-33 所示，我们在深度方向（垂直方向）上插入 Dropout 层。

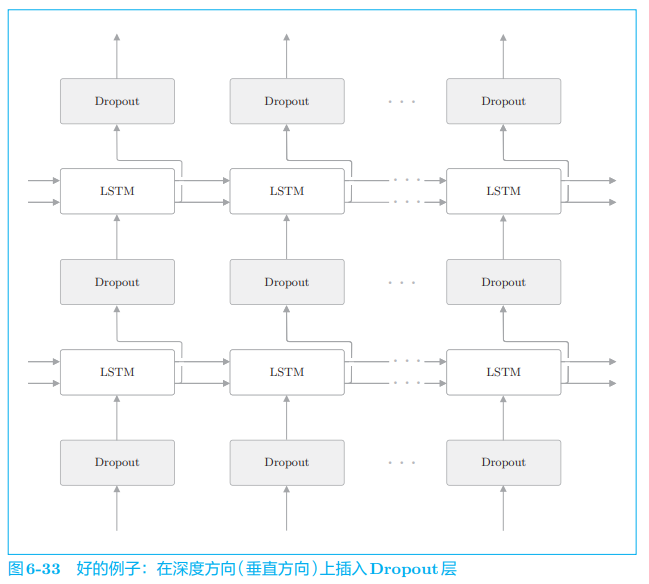
这样一来，无论沿时间方向（水平方向）前进多少，信息都不会丢失。 Dropout 与时间轴独立，仅在深度方向（垂直方向）上起作用。

6.5.3 权重共享

改进语言模型有一个非常简单的技巧，那就是权重共享（weight tying）。 weight tying 可以直译为 “权重绑定”。如图 6-35 所示，其含义就是共享权重。

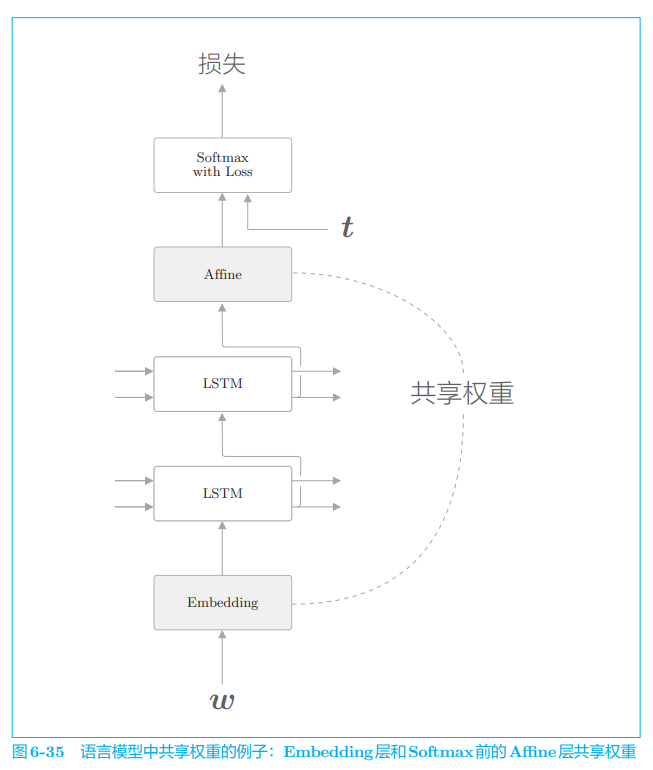
如图 6-35 所示，绑定（共享）Embedding 层和 Affine 层的权重的技巧在于权重共享。通过在这两个层之间共享权重，可以大大减少学习的参数数量。尽管如此，它仍能提高精度。真可谓一石二鸟！

现在，我们来考虑一下权重共享的实现。这里，假设词汇量为 V， LSTM 的隐藏状态的维数为 H，则 Embedding 层的权重形状为 V × H， Affine 层的权重形状为 H × V。此时，如果要使用权重共享，只需将 Embedding 层权重的转置设置为 Affine 层的权重。这个非常简单的技巧可以带来出色的结果。

为什么说权重共享是有效的呢？直观上，共享权重可以减少需要学习的参数数量，从而促进学习。另外，参数数量减少，还能收获抑 制过拟合的好处。

6.5.4 更好的RNNLM的实现

见书