机器学习:皮尔逊相关系数——影评相关性分析案例

机器学习:皮尔逊相关系数——影评相关性分析案例
文章目录
- 机器学习:皮尔逊相关系数——影评相关性分析案例
-
- :rocket:1、皮尔逊相关系数概念及公式
- :rocket:2、案例
-
- 代码部分
皮尔逊(pearson)相关系数、
斯皮尔曼(spearman)相关系数和
肯德尔(kendall)相关系数并称为统计学三大相关系数。这里我们来谈一谈皮尔逊(pearson)相关系数的公式及应用
🚀1、皮尔逊相关系数概念及公式
在统计学中,皮尔逊相关系数( Pearson correlation coefficient),又称皮尔逊积矩相关系数(Pearson product-moment correlation coefficient,简称 PPMCC或PCCs),是用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间,0表示没有相关性。
公式:
ρX,Y=cov(X,y)σXσY=E((X−μx)(Y−μY))σXσY=E(XY)−E(X)E(Y)E(X2)−E2(X)E(Y2)−E2(Y)\\rho_{X,Y}=\\frac{cov(X,y)}{\\sigma_X\\sigma_Y}=\\frac{E((X-\\mu_x)(Y-\\mu_Y))}{\\sigma_X\\sigma_Y}=\\frac{E(XY)-E(X)E(Y)}{\\sqrt{E(X^2)-E^2(X)}{\\sqrt{E(Y^2)-E^2(Y)}}} ρX,Y=σXσYcov(X,y)=σXσYE((X−μx)(Y−μY))=E(X2)−E2(X)E(Y2)−E2(Y)E(XY)−E(X)E(Y)
通过计算协方差与标准差的商,来得出相关系数。小于0时为负相关,大于0时为正相关。
🚀2、案例
我随便写了一个影评数据集做demo
| 老炮儿 | 唐人街探案 | 星球大战 | 寻龙诀 | 神探夏洛克 | 小门神 |
|---|---|---|---|---|---|
| 3.5 | 1 | 0 | 0 | 0 | 0 |
| 2.5 | 3.5 | 3 | 3.5 | 2.5 | 3 |
| 3 | 3.5 | 1.5 | 5 | 3 | 3.5 |
| 2.5 | 3.5 | 0 | 3.5 | 4 | 0 |
| 3.5 | 2 | 4.5 | 0 | 3.5 | 2 |
| 3 | 4 | 2 | 3 | 3 | 2 |
| 4.5 | 1.5 | 3 | 5 | 3.5 | 0 |
代码部分
*首先引入pandas来让我的数据处理变得简单*
import pandas
import pandas as pd
*随后引入scipy库中封装好的皮尔森系数方法*
from scipy.stats import pearsonr
*计算皮尔逊相关系数矩阵*
def calculate_pearson_correlation(data):data = pandas.DataFrame(data)correlations = data.corr(method='pearson')return correlations
def GetPvalue_Pearson(x,y):return pearsonr(x,y)[1]
*返回相关系数检验P值矩阵*
def calculate_person_correlation_P(data):data = pd.DataFrame(data)return data.corr(method=GetPvalue_Pearson)
*读取文件,由于有中文表头,所以设置gbk编码*
*最后输出相关系数矩阵*
data = pd.read_csv("movie_sperman.csv",encoding='gbk')
res = calculate_pearson_correlation(data)
res
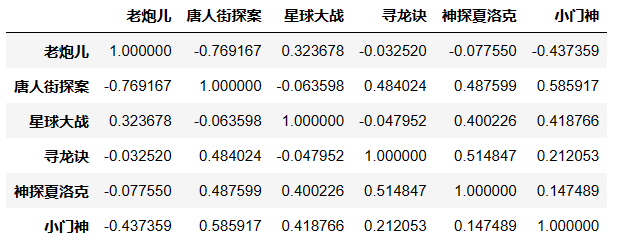
plt.rcParams['font.sans-serif'] = 'Microsoft Yahei'
ax = plt.subplots(figsize=(20, 16))#调整画布大小
ax = sns.heatmap(res, vmax=.8, square=True, annot=True)#画热力图 annot=True 显示系数
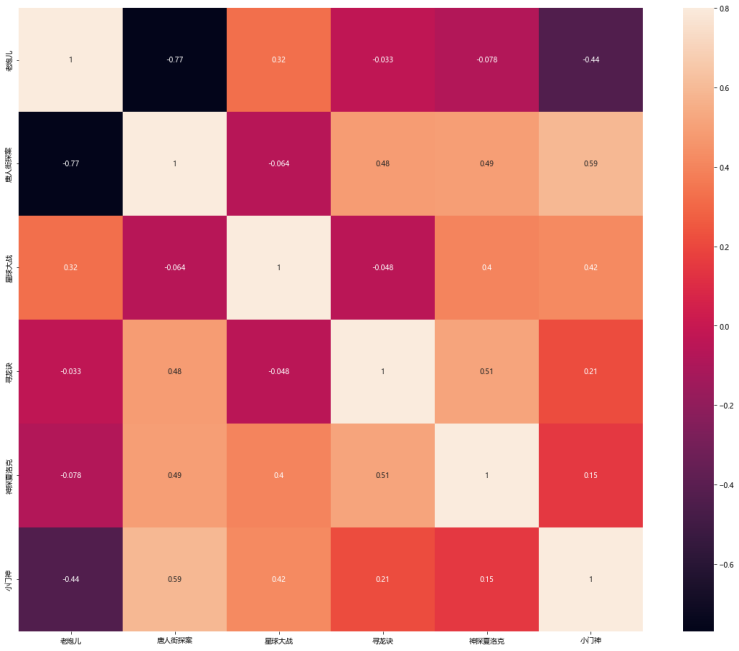
由于是相关性矩阵,所以我绘制了热力图。
可以看到颜色越深,相关性越大。
例如,唐人街探案与老炮的影评数据相关性为-0.77呈负相关,所以可以简单地推出喜欢唐人街探案的人不喜欢老炮。(非真实数据结论)


