AtCoder Beginner Contest 295——F - substr = S

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello, 大家好哇！本初中生蒟蒻讲解一下AtCoder Beginner Contest 295这场比赛的F题！

===========================================================================================

F - substr = S

原题

Problem Statement

You are given a string $S$ consisting of digits and positive integers $L$ and $R$ for each of $T$ test cases. Solve the following problem.
For a positive integer $x$, let us define $f(x)$ as the number of contiguous substrings of the decimal representation of $x$ (without leading zeros) that equal $S$.
For instance, if $S=$ 22, we have $f(122)=1$, $f(123)=0$, $f(226)=1$, and $f(222)=2$.
Find ∑k=LRf(k)\\displaystyle \\sum_{k=L}^{R} f(k)k=L∑R​f(k).

Constraints

$1\le T\le 1000$
$S$ is a string consisting of digits whose length is between $1$ and $16$, inclusive.
$L$ and $R$ are integers satisfying 1≤L≤R;10161 \\le L \\le R ; 10^{16}1≤L≤R;1016.

Input

The input is given from Standard Input in the following format, where casei\\rm{case}_icasei​ denotes the $i$-th test case:
$T$
case1\\rm{case}_{1}case1​
case2\\rm{case}_{2}case2​
$⋮$
caseT\\rm{case}_{\\it{T}}caseT​
Each test case is in the following format:
$S$ $L$ $R$

Output

Print $T$ lines in total.

The $i$-th line should contain an integer representing the answer to the $i$-th test case.

Sample Input 1

6
22 23 234
0295 295 295
0 1 9999999999999999
2718 998244353 9982443530000000
869120 1234567890123456 2345678901234567
2023032520230325 1 9999999999999999

Sample Output 1

12
0
14888888888888889
12982260572545
10987664021
1
This input contains six test cases.
In the first test case, $S=$ 22, $L=23$, $R=234$.
$f(122)=f(220)=f(221)=f(223)=f(224)=\cdots =f(229)=1$.
$f(222)=2$.
Thus, the answer is $12$.
In the second test case, $S=$ 0295, $L=295$, $R=295$.
Note that $f(295)=0$.

题目大意

本题是求∑k=LRf(k)\\displaystyle \\sum_{k=L}^{R} f(k)k=L∑R​f(k)
$f(k)=k$这个数转换为字符串后，出现S的个数
例如：$k=222,S=22$
则$f(k)=2$

思路

本题让我们求∑k=LRf(k)\\displaystyle \\sum_{k=L}^{R} f(k)k=L∑R​f(k)
那么可以利用前缀和的思想转化为求∑k=1Rf(k)−∑k=1L−1f(k)\\displaystyle \\sum_{k=1}^{R}f(k) - \\displaystyle \\sum_{k=1}^{L - 1}f(k)k=1∑R​f(k)−k=1∑L−1​f(k)

所以我们的主要任务就是求∑k=1Xf(k)(1≤X≤1016)\\displaystyle \\sum_{k=1}^{X}f(k)(1\\le X \\le 10^{16})k=1∑X​f(k)(1≤X≤1016)

然后我们可以构造$k$，对于有值的$f(k)$那么一定是包含$S$的，那么我们可以枚举$S$在哪一位，因为一共就只有16位。
如图：

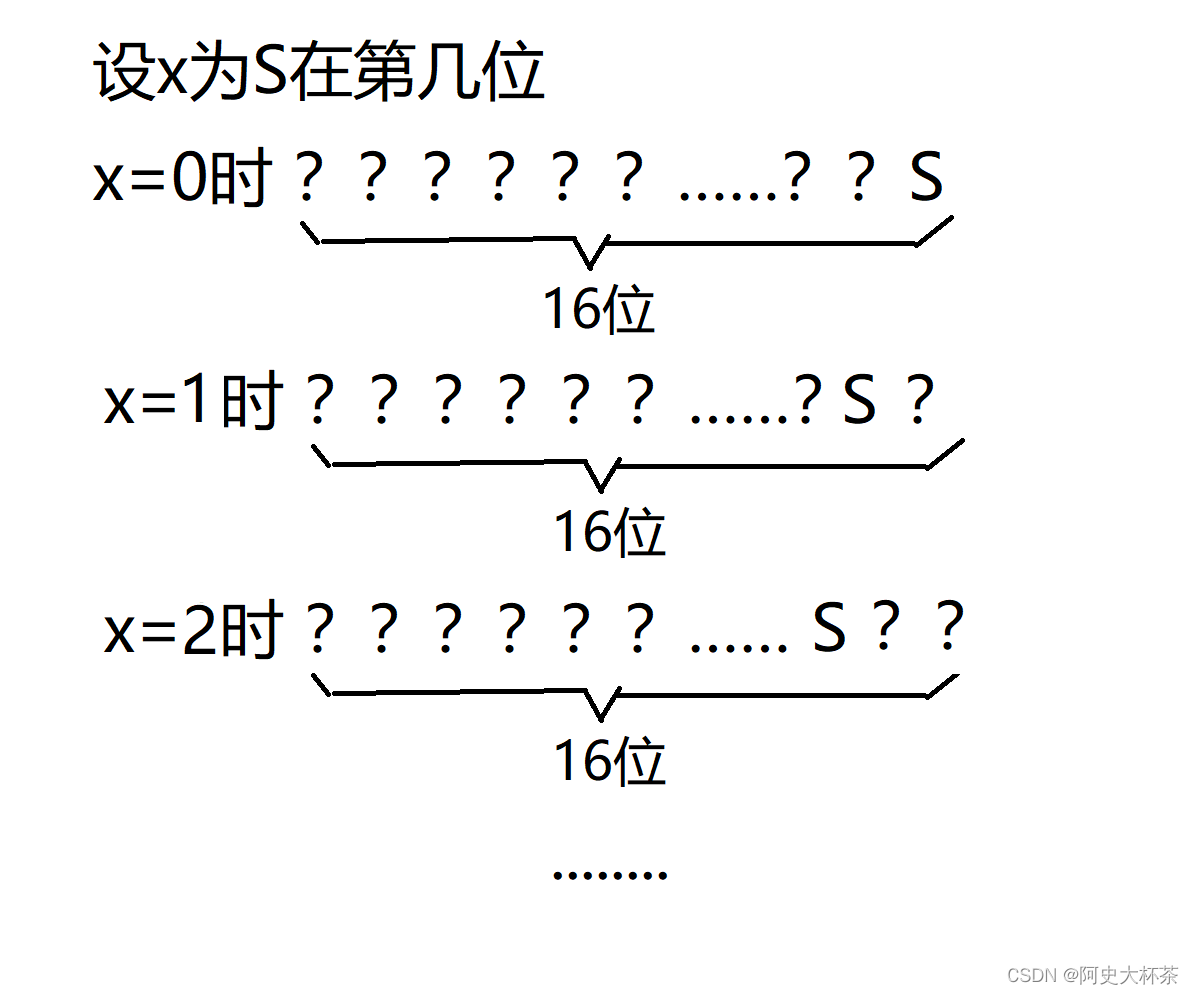
情况一：S没有前导零

我们相应的计算S在每一位上有多少个数：（注意：这里位数是从0开始的,这里k相当于前面的X）

于是我们就可以设i为从S在第k位第第i小的数，此处我们还是以S = 95为例 (注意：这里位数是从0开始的,这里k相当于前面的X)

这样，我们就能精准的计算出有没有越界（即为这个数有没有大于$X$）

情况二：S有前导零

我们可以为了以防出现$S=05,k=1,i=0$结果算成了$f(5)=1$这样的情况发生

我们可以在前面补个S的前面补充一个1。如$S=05$
$i=1,k=3$时，就是10500
所以我们不再是和情况一样是$i-1$，而是i−1+10ri-1+10^ri−1+10r
$r=k+1-|S|$（$|S|$表示S的长度）

例如，$S=05,i=151,k=3$时：
$r=3+1-2=2$
所以填写的就是：i−1+10r=150+102=150+100=250i-1+10^r=150+10^2=150+100=250i−1+10r=150+102=150+100=250

所以对应填入：

之后，我们可以用一个函数$number(i,k,s)$表示$k$位填充$S$后，第$i$小的数。之后通过二分找到最大的没有超过边界的数，然后加上这个最大的$i$即可。最后把答案累加！
具体看代码吧

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
#define endl '\\n'
#define psb(i) push_back(i)
#define ppb() pop_back()
#define psf(i) push_front(i)
#define ppf() pop_front()
#define ps(i) push(i)using namespace std;typedef pair<int, int> PII;const int N = 2e1 + 10;int T;
string s;
int l, r;
int p10[N];inline int read()
{int w = 1, s = 0;char c = getchar();while (c < '0' || c > '9'){if (c == '-') w = -1;c = getchar();}while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();return w * s;
}inline void init()
{p10[0] = 1;for (int i = 1; i <= 16; i ++)p10[i] = p10[i - 1] * 10;
}int number(int i, int k, string s)
{int r = k + 1 - s.size();if (r < 0) return -1;if (s[0] == '0') i += p10[r];i --;int p = i / p10[r]; //有前导零补得数int q = i % p10[r];return p * p10[k + 1] + stoll(s) * p10[r] + q;
}inline int solve(int x, string s)
{int res = 0;for (int k = 0; k <= 15; k ++){int first = number(1, k, s);if (first == -1 || first > x) continue;int l = 1, r = p10[16 - s.size()];while (l <= r){int fd = l + r >> 1;if (number(fd, k, s) > x) r = fd - 1;else l = fd + 1;}res += r;}return res;
}signed main()
{cin.tie(0);cout.tie(0);ios::sync_with_stdio(0);init();cin >> T;while (T --){cin >> s >> l >> r;cout << solve(r, s) - solve(l - 1, s) << endl;}return 0;
}

今天就到这里了！

大家有什么问题尽管提，我都会尽力回答的！

吾欲您伸手，点的小赞赞。吾欲您喜欢，点得小关注！