不要纠结，干就完事了，熟练度很重要！！！多练习，多总结！！！

纲领篇

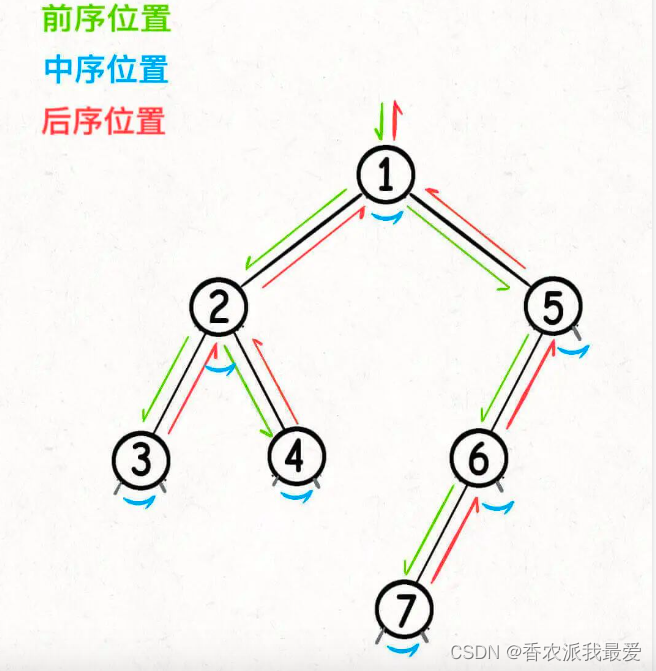
二叉树的所有问题，就是让你在前中后序位置注入巧妙的代码逻辑，去达到自己的目的，你只需要单独思考每一个节点应该做什么，其他的不用你管，抛给二叉树遍历框架，递归会在所有节点上做相同的操作。

二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题计算出答案，这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。

前序位置是刚刚进入节点的时刻，后序位置是即将离开节点的时刻。意味着前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。

后序位置的特点，只有后序位置才能通过返回值获取子树的信息。一旦你发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

LeetCode 104. 二叉树的最大深度

解题思路

法一：显然遍历一遍二叉树，用一个外部变量记录每个节点所在的深度，取最大值就可以得到最大深度，这就是遍历二叉树计算答案的思路。

法二：很容易发现一棵二叉树的最大深度可以通过子树的最大高度推导出来，这就是分解问题计算答案的思路。

代码实现

法一

class Solution {public int maxDepth(TreeNode root) {if(root == null){return 0;}int left = maxDepth(root.left);int right = maxDepth(root.right);return Math.max(left, right)+1;}
}

法二

// 记录最大深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;// 主函数
int maxDepth(TreeNode root) {traverse(root);return res;
}// 二叉树遍历框架
void traverse(TreeNode root) {if (root == null) {// 到达叶子节点，更新最大深度res = Math.max(res, depth);return;}// 前序位置depth++;traverse(root.left);traverse(root.right);// 后序位置depth--;
}

遇到一道二叉树的题目时的通用思考过程是：

1. 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个traverse函数配合外部变量来实现。
2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。
3. 无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

LeetCode 543. 二叉树的直径

解题思路

每一条二叉树的「直径」长度，就是一个节点的左右子树的最大深度之和。
现在让我求整棵树中的最长「直径」，那直截了当的思路就是遍历整棵树中的每个节点，然后通过每个节点的左右子树的最大深度算出每个节点的「直径」，最后把所有「直径」求个最大值即可。

代码实现

class Solution {int maxDia = 0;public int diameterOfBinaryTree(TreeNode root) {maxDep(root);return maxDia;}public int maxDep(TreeNode root){if(root == null){return 0;}int left = maxDep(root.left);int right = maxDep(root.right);maxDia = Math.max(maxDia, left+right);return 1+Math.max(left, right);}
}

LeetCode 124. 二叉树中的最大路径和

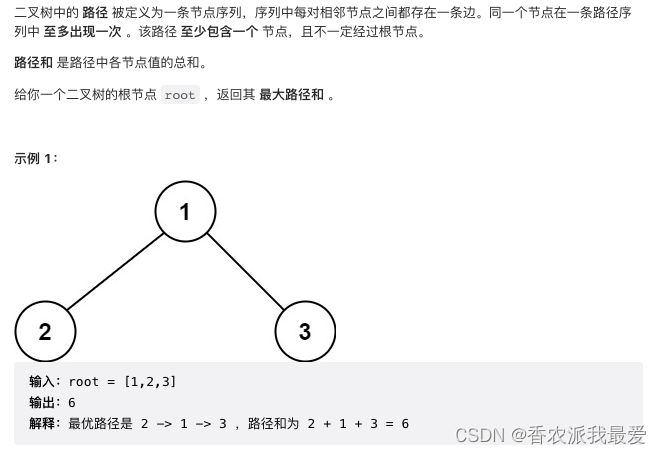
解题思路

参考LeetCode 543. 二叉树的直径

代码实现

class Solution {int pathMax = Integer.MIN_VALUE;public int maxPathSum(TreeNode root) {pathNum(root);return pathMax;}public int pathNum(TreeNode root){if(root == null){return 0;}int left = Math.max(pathNum(root.left), 0);int right = Math.max(pathNum(root.right), 0);pathMax = Math.max(left+right+root.val, pathMax);return Math.max(left, right)+root.val;}
}

LeetCode 144. 二叉树的前序遍历

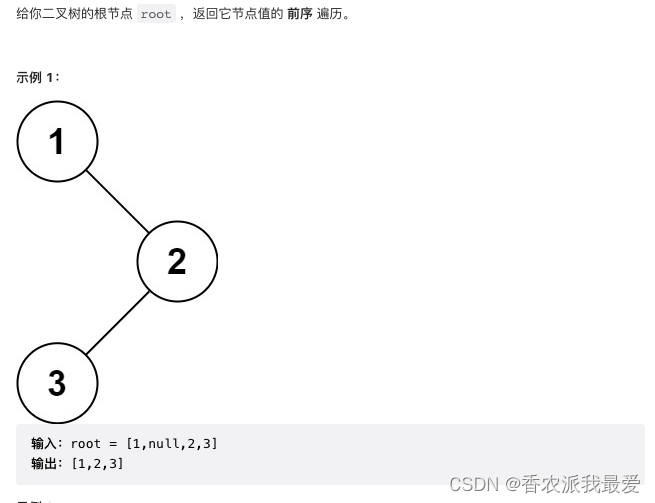
代码实现

class Solution {List<Integer> res = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {traverse(root);return res;}public void traverse(TreeNode root){if(root == null){return ;}res.add(root.val);traverse(root.left);traverse(root.right);}}

二叉树层序遍历

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode root) {if (root == null) return;Queue<TreeNode> q = new LinkedList<>();q.offer(root);// 从上到下遍历二叉树的每一层while (!q.isEmpty()) {int sz = q.size();// 从左到右遍历每一层的每个节点for (int i = 0; i < sz; i++) {TreeNode cur = q.poll();// 将下一层节点放入队列if (cur.left != null) {q.offer(cur.left);}if (cur.right != null) {q.offer(cur.right);}}}
}

思维篇

LeetCode 226. 翻转二叉树

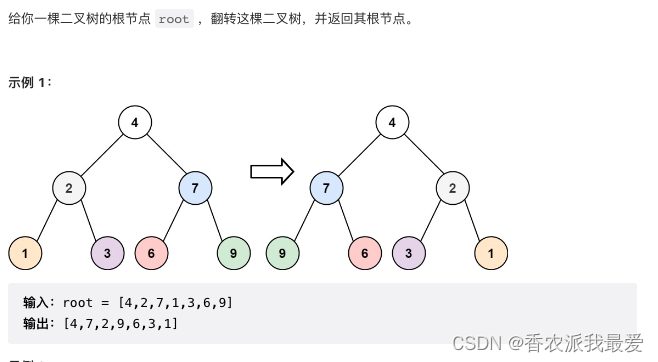
解题思路

法一：这题能不能用「遍历」的思维模式解决？
可以，我写一个traverse函数遍历每个节点，让每个节点的左右子节点颠倒过来就行了。
单独抽出一个节点，需要让它做什么？让它把自己的左右子节点交换一下。
需要在什么时候做？好像前中后序位置都可以。

法二：这题能不能用「分解问题」的思维模式解决？
我们尝试给invertTree函数赋予一个定义：

// 定义：将以 root 为根的这棵二叉树翻转，返回翻转后的二叉树的根节点
TreeNode invertTree(TreeNode root);

然后思考，对于某一个二叉树节点x执行invertTree(x)，你能利用这个递归函数的定义做点啥？
我可以用invertTree(x.left)先把x的左子树翻转，再用invertTree(x.right)把x的右子树翻转，最后把x的左右子树交换，这恰好完成了以x为根的整棵二叉树的翻转，即完成了invertTree(x)的定义。

代码实现

法一：

class Solution {public TreeNode invertTree(TreeNode root) {traverse(root);return root;}public TreeNode traverse(TreeNode root){if(root == null){return null;}traverse(root.left);traverse(root.right);TreeNode tmp = root.left;root.left = root.right;root.right = tmp;return root;}
}

法二：

// 定义：将以 root 为根的这棵二叉树翻转，返回翻转后的二叉树的根节点
TreeNode invertTree(TreeNode root) {if (root == null) {return null;}// 利用函数定义，先翻转左右子树TreeNode left = invertTree(root.left);TreeNode right = invertTree(root.right);// 然后交换左右子节点root.left = right;root.right = left;// 和定义逻辑自恰：以 root 为根的这棵二叉树已经被翻转，返回 rootreturn root;
}

LeetCode 116. 填充每个节点的下一个右侧节点指针

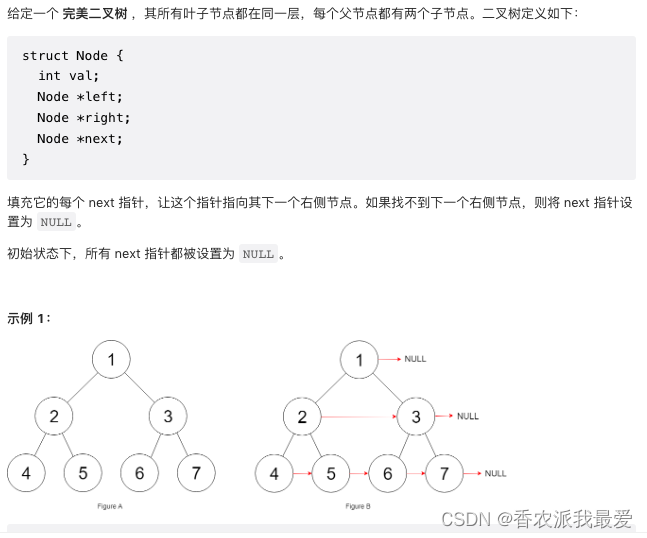
解题思路

这题能不能用「遍历」的思维模式解决？
很显然，一定可以。
每个节点要做的事也很简单，把自己的next指针指向右侧节点就行了。

传统的traverse函数是遍历二叉树的所有节点，但现在我们想遍历的其实是两个相邻节点之间的「空隙」。
可以在二叉树的基础上进行抽象，你把图中的每一个方框看做一个节点：

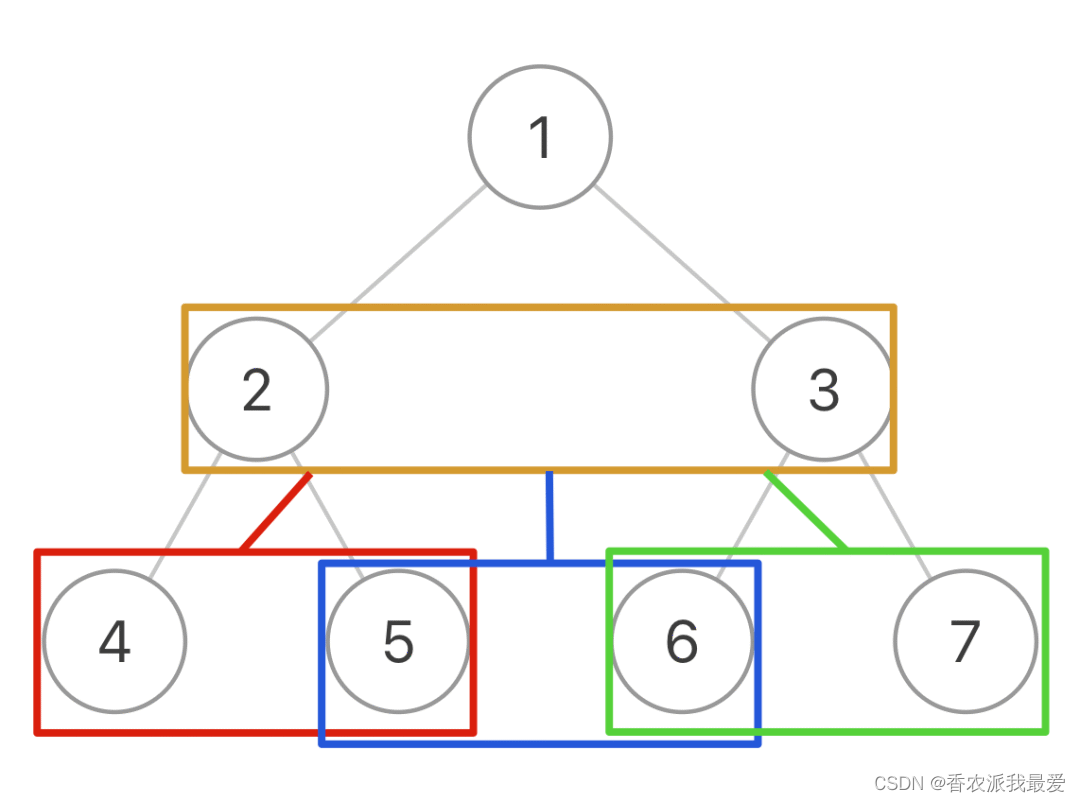
一棵二叉树被抽象成了一棵三叉树，三叉树上的每个节点就是原先二叉树的两个相邻节点。
现在，我们只要实现一个traverse函数来遍历这棵三叉树，每个「三叉树节点」需要做的事就是把自己内部的两个二叉树节点穿起来：

代码实现

class Solution {public Node connect(Node root) {if(root == null){return null;}traverse(root.left, root.right);return root;}public void traverse(Node node1, Node node2){if(node1==null || node2== null){return ;}node1.next=node2;traverse(node1.left, node1.right);traverse(node2.left, node2.right);traverse(node1.right, node2.left);return ;}
}

LeetCode 114. 二叉树展开为链表

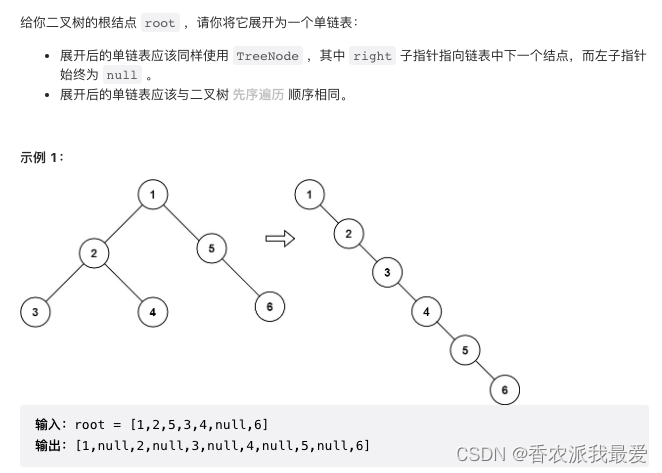
解题思路

这题能不能用「分解问题」的思维模式解决？尝试给出flatten函数的定义：

// 定义：输入节点 root，然后 root 为根的二叉树就会被拉平为一条链表
void flatten(TreeNode root);

有了这个函数定义，如何按题目要求把一棵树拉平成一条链表？
对于一个节点x，可以执行以下流程：

1. 先利用flatten(x.left)和flatten(x.right)将x的左右子树拉平。
2. 将x的右子树接到左子树下方，然后将整个左子树作为右子树。

代码实现

class Solution {public void flatten(TreeNode root) {if(root == null){return ;}flatten(root.left);flatten(root.right);TreeNode left = root.left;TreeNode right = root.right;root.left=null;root.right=left;TreeNode p = root;while(p.right != null){p = p.right;}p.right = right;}
}

总结

本题来源于Leetcode中 归属于二叉树类型题目。
同许多在算法道路上不断前行的人一样，不断练习，修炼自己！
如有博客中存在的疑问或者建议，可以在下方留言一起交流，感谢各位！

觉得本博客有用的客官，可以给个点赞+收藏哦！ 嘿嘿

喜欢本系列博客的可以关注下，以后除了会继续更新面试手撕代码文章外，还会出其他系列的文章！