Every day a leetcode

题目来源：135. 分发糖果

解法1：贪心

首先把所有孩子的糖果数初始化为1。

从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的糖果数加1。

再从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数不大于右边孩子的糖果数，则左边孩子的糖果数更新为右边孩子的糖果数加1。

代码：

#include <iostream>
using namespace std;int candy(int *ratings, int ratingsSize);int main()
{int n;cin >> n;int a[n];for (int i = 0; i < n; i++)cin >> a[i];cout << candy(a, n) << endl;system("pause");return 0;
}int candy(int *ratings, int ratingsSize)
{int n = ratingsSize;int candy[n];for (int i = 0; i < n; i++) // 每个孩子至少分配到1个糖果{candy[i] = 1;// cout << candy[i] << " ";}// cout << endl;// 从左往右遍历一遍，如果右边孩子的评分比左边的高，则右边孩子的糖果数更新为左边孩子的糖果数加1for (int i = 0; i < n - 1; i++)if (ratings[i] < ratings[i + 1])candy[i + 1] = candy[i] + 1;// 从右往左遍历一遍，如果左边孩子的评分比右边的高，且左边孩子当前的糖果数不大于右边孩子的糖果数，// 则左边孩子的糖果数更新为右边孩子的糖果数加1for (int i = n - 1; i > 0; i--)if (ratings[i - 1] > ratings[i] && candy[i - 1] <= candy[i])candy[i - 1] = candy[i] + 1;// 统计糖果总数int sum = 0;for (int i = 0; i < n; i++)sum += candy[i];return sum;
}

结果：

复杂度分析：

时间复杂度：O(n)，其中n是孩子的数量。我们需要遍历两次数组以分别计算满足左规则或右规则的最少糖果数量。

空间复杂度：O(n)，其中n是孩子的数量。我们需要candy数组储存糖果数。

解法2：常数空间遍历

注意到糖果总是尽量少给，且从1开始累计，每次要么比相邻的同学多给一个，要么重新置为1。

依据此规则，我们可以画出下图：

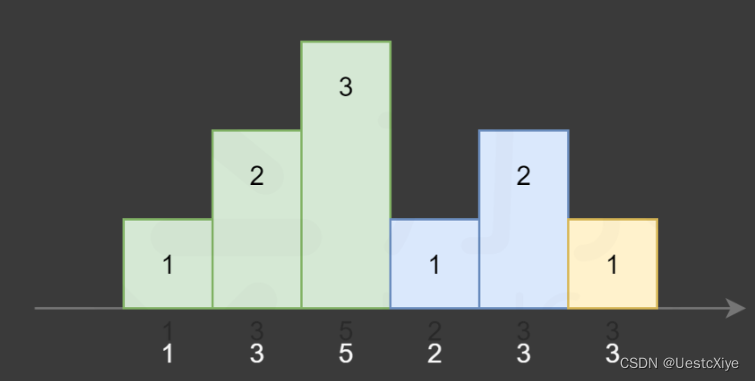
其中相同颜色的柱状图的高度总恰好为1，2，3，…。

而高度也不一定一定是升序，也可能是…，3，2，1。

注意到在上图中，对于第三个同学，他既可以被认为是属于绿色的升序部分，也可以被认为是属于蓝色的降序部分。因为他同时比两边的同学评分更高。我们对序列稍作修改：

注意到右边的升序部分变长了，使得第三个同学不得不被分配4个糖果。

依据前面总结的规律，我们可以提出本题的解法。我们从左到右枚举每一个同学，记前一个同学分得的糖果数量为pre：

如果当前同学比上一个同学评分高，说明我们就在最近的递增序列中，直接分配给该同学pre+1个糖果

否则我们就在一个递减序列中，我们直接分配给当前同学一个糖果，并把该同学所在的递减序列中所有的同学都再多分配一个糖果，以保证糖果数量还是满足条件。

我们无需显式地额外分配糖果，只需要记录当前的递减序列长度，即可知道需要额外分配的糖果数量。

同时注意当当前的递减序列长度和上一个递增序列等长时，需要把最近的递增序列的最后一个同学也并进递减序列中。

这样，我们只要记录当前递减序列的长度dec，最近的递增序列的长度inc和前一个同学分得的糖果数量pre即可。

代码：

int candy(int* ratings, int ratingsSize) {int ret = 1;int inc = 1, dec = 0, pre = 1;for (int i = 1; i < ratingsSize; i++) {if (ratings[i] >= ratings[i - 1]) {dec = 0;pre = ratings[i] == ratings[i - 1] ? 1 : pre + 1;ret += pre;inc = pre;} else {dec++;if (dec == inc) {dec++;}ret += dec;pre = 1;}}return ret;
}

复杂度分析：

时间复杂度：O(n)，其中n是孩子的数量。我们需要遍历1次数组。

空间复杂度：O(1)。我们只需要常数的空间保存若干变量。