蓝桥杯已经结束，打下来很难受。自己对于算法的掌握还是不够，遂继续开启博客书写，激励自己学习。本系列文章以牛客数据结构课程为基础，记录自己对于课程的理解和部分代码。供自己学习复习使用！

基础前缀和

int a[N],s[N];//前缀和数组
s[i]=s[i-1]+a[i];//s[i]表示a1+a2+...+ai
所以查询[l,r]的值之和就可以s[r]-s[l-1]

基础差分

差分数组b[i]=a[i]-a[i-1]
所以对差分数组求前缀和就可以得到原数组。
差分数组一般用来维护给一段区间加上或减去一直相同的值
比如给[l,r]区间的每个值都加上c
void insert(int l, int r, int c)
{b[l] += c;b[r + 1] -= c;
}
构造差分数组 for(int i=1;i<=n;i++) insert(i,i,a[i]);
或者 for(int i=1;i<=n;i++) b[i]=a[i]-a[i-1];
最后对b数组求一次前缀和就可以得到结果对原数组差分后可以发现正数之和加上负数之和等于0

区间乘积

智乃酱的区间乘积
由于乘法运算也是可差分的。所以我们配合逆元便可以求区间乘积。

int n,m;
int a[N],s[N];
int qmi(int a,int k,int p){int res=1%p;a%=p;while(k){if(k&1) res=(LL)res*a%p;a=(LL)a*a%p;k>>=1;}return res;
}
void Showball(){cin>>n>>m;s[0]=1;for(int i=1;i<=n;i++){cin>>a[i];s[i]=(LL)s[i-1]*a[i]%mod;}int l,r;while(m--){cin>>l>>r;cout<<(LL)s[r]*qmi(s[l-1],mod-2,mod)%mod<<endl;}
}

前缀置换

对于一些置换，如果我们也可以通过一些方式将它还原回去，那么我们就可以进行类似前缀和的操作，比如矩阵和矩阵求逆等等。
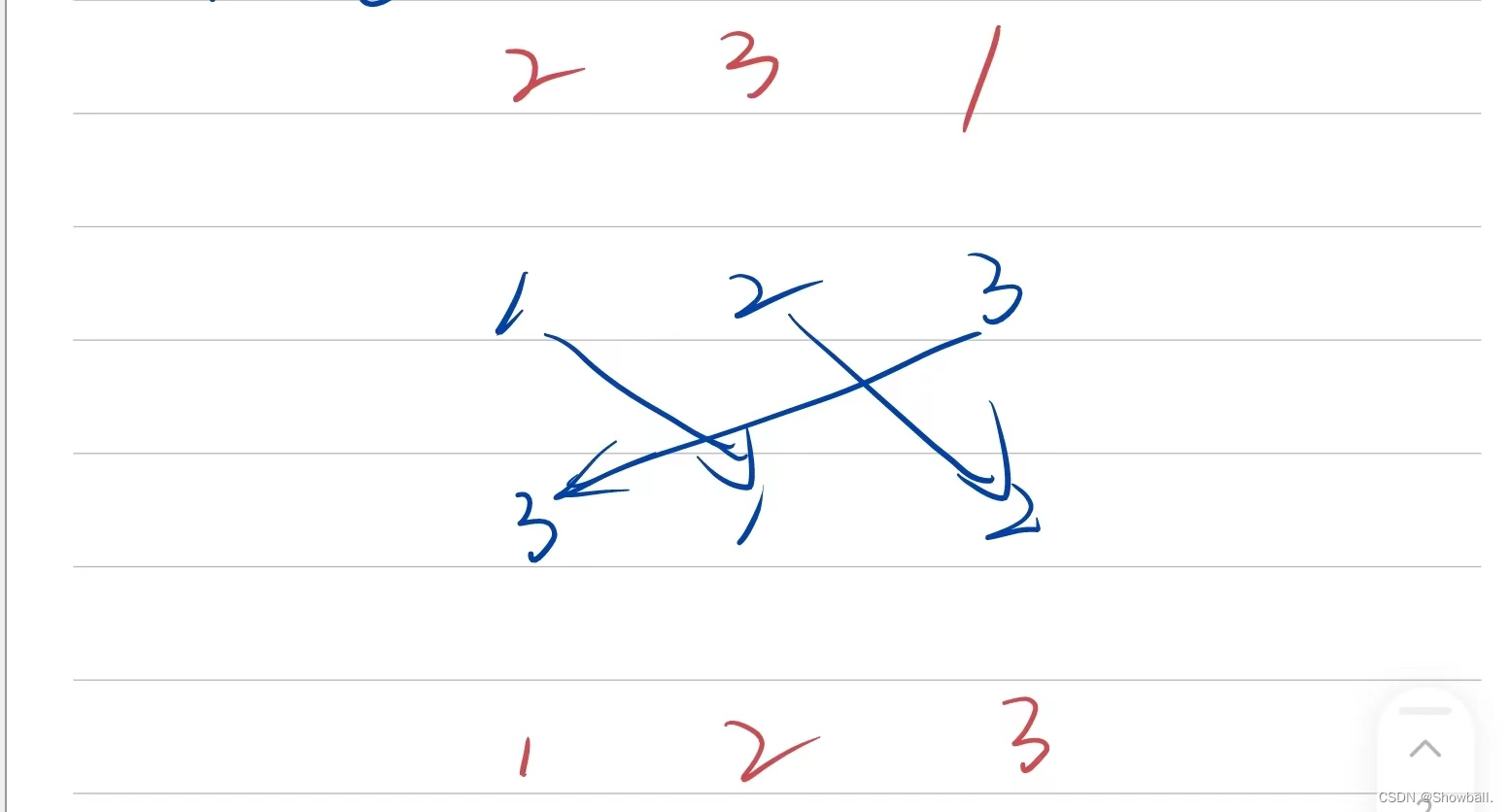
牛牛的猜球游戏

对于这道题目，我们发现对于每次交换操作，我们可以通过下标转换消去操作带来的影响，那么我们就可以进行类似前缀和的操作进行维护。

int n,m;
int s[N][10];
void Showball(){cin>>n>>m;for(int i=0;i<10;i++) s[0][i]=i;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;memcpy(s[i],s[i-1],sizeof s[i]);swap(s[i][x],s[i][y]);}int l,r;while(m--){cin>>l>>r;int p[10];for(int i=0;i<10;i++) p[s[l-1][i]]=i;for(int i=0;i<10;i++) cout<<p[s[r][i]]<<" \\n"[i==9];}
}

智乃酱的双塔问题
这个题目就涉及到了矩阵的前缀和操作。
贴一个大佬的题解

这里贴一个线段树做法

#include<bits/stdc++.h>
using namespace std;const int N=1e5+10,M=2;
const int mod=1e9+7;
int n,m;char s[N];
struct node{int l,r;int mat[M][M];
}tr[N*4];void mul(int c[M][M],int a[M][M],int b[M][M]){int ans[M][M];memset(ans,0,sizeof ans);for(int i=0;i<M;i++){for(int j=0;j<M;j++){for(int k=0;k<M;k++){ans[i][j]=(ans[i][j]+1LL*a[i][k]*b[k][j])%mod;}}}memcpy(c,ans,sizeof ans);
}
void pushup(node &u,node &l,node &r){mul(u.mat,l.mat,r.mat);
}void pushup(int u){pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}void build(int u,int l,int r){tr[u]={l,r};if(l==r){if(s[r]=='/'){auto &t=tr[u].mat;t[0][0]=t[0][1]=t[1][1]=1;t[1][0]=0;}else{auto &t=tr[u].mat;t[0][0]=t[1][0]=t[1][1]=1;t[0][1]=0;}return;}int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);
}node query(int u,int l,int r){if(l<=tr[u].l&&tr[u].r<=r) return tr[u];int mid=tr[u].l+tr[u].r>>1;if(r<=mid) return query(u<<1,l,r);if(l>mid) return query(u<<1|1,l,r);node res;node left=query(u<<1,l,r);node right=query(u<<1|1,l,r);pushup(res,left,right);return res;
}
int main(){cin>>n>>m;for(int i=1;i<n;i++){cin>>s[i];}build(1,1,n-1);while(m--){int hs,ht,ps,pt;cin>>hs>>ht>>ps>>pt;cout<<query(1,hs,ht-1).mat[ps][pt]<<endl;}return 0;
}

经典差分性质题目

[NOIP2013]积木大赛
[NOIP2018]道路铺设
两道题目题意相似：都是有不同高度的积木，每次可以给一个区间加1，求最少操作构成积木。

差分性质：

我们给原数组后面补一位0。这样我们发现差分数组的正数之和绝对值和负数之和绝对值相等。
而我们给一段区间加上1，相当于给差分数组一个值+1，一个值-1。那么最小的操作次数自然就为差分数组所有正数元素之和。

void Showball(){int n;cin>>n;vector<int> a(n+2),b(n+2);for(int i=1;i<=n;i++) cin>>a[i];int ans=0;for(int i=1;i<=n+1;i++){b[i]=a[i]-a[i-1];if(b[i]>0) ans+=b[i];}cout<<ans<<endl;
}

前缀和变种

前缀和+等差数列
对于一个等差数列 1 2 3 4 5 …
我们对其进行一次差分得到 1 1 1 1 1…
再进行一次差分即1 0 0 0 0 …
所以如果我们想要对于某一段区间加上 1,2,3,4,5,…
我们可以对它的二次差分数组该位加上1，然后求两次前缀和即可

前缀和+平方
同理 对于一个平方数列 1 4 9 16 25 …
我们对其进行一次差分得到 1 3 5 7 9 …
再进行一次差分得到 1 2 2 2 2 2…
再进行一次差分得到 1 1 0 0 0 0 …
所以如果我们想要对于某一段区间加上 1,4,9,16,25,…
我们可以对它的三次差分数组该位和下一位都加上1，然后求三次前缀和即可。

先来一道模板题
小w的糖果
三种操作分别对应普通区间加，区间加等差数列，区间加平方数列。
这里我们构建三个差分数组，然后进行对应操作即可。

#include<bits/stdc++.h>using namespace std;#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\\n'
#define debug(x) cout<<#x<<":"<<x<<endl;typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;
const int cases = 1;int n,m;
LL d1[N],d2[N],d3[N];
void presum(LL d[]){for(int i=1;i<=n;i++){d[i]+=d[i-1];if(d[i]>mod) d[i]-=mod;}
}
void Showball(){cin>>n>>m;memset(d1,0,sizeof d1);memset(d2,0,sizeof d2);memset(d3,0,sizeof d3);int t,p;while(m--){cin>>t>>p;if(t==1){d1[p]++;}else if(t==2){d2[p]++;}else{d3[p]++;d3[p+1]++;  }}presum(d1);presum(d2);presum(d2);presum(d3);presum(d3);presum(d3);for(int i=1;i<=n;i++){cout<<(d1[i]+d2[i]+d3[i]+mod)%mod<<" \\n"[i==n];}
}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int T=1;if(cases) cin>>T;while(T--)Showball();return 0;
}

牛牛的Link Power I
题意：给你一个只含有0和1的字符串，两个1之间的距离为贡献。请你算出所有的贡献值之和。
举个例子：1010010
答案：2+5+3=10
我们算出每个1对于后面1的贡献,然后想加即可。
我们先看第一个1，然后我们发现第一个1对于后面的贡献分别为1 2 3 4 5 …
由此我们想到了上面讲到的前缀和+等差数列,我们可以对于每一个为1的位置加上一个等差数列。最后进行求前缀和。然后加上每一个1位置的值（也就是对应贡献）。即为答案。

int n;
LL sum[N];
string s;
void presum(){//求前缀和for(int i=0;s[i];i++){sum[i]+=sum[i-1];if(sum[i]>mod) sum[i]-=mod;}
}
void Showball(){cin>>n;cin>>s;for(int i=0;s[i];i++){if(s[i]=='1') sum[i+1]=1;//根据之前的性质，我们给差分数组的下一个位置+1。}presum();presum();//对差分数组求两次前缀和，得到原数组LL ans=0;for(int i=0;s[i];i++){if(s[i]=='1') ans+=sum[i];//对于等于1的位置，加上对应贡献if(ans>mod) ans-=mod;//取模}cout<<ans<<endl;
}

区间加多项式
之前我们处理的问题都是特殊情况，现在来考虑一般情况。给一段区间上加上一个多项式。我们还是按照之前的方式进行差分。可以发现对于任意一个最高次为k的多项式，我们对其进行k+1次差分，它一定会变成有限几项后面全为0的形式。那么我们就可以维护差分数组，然后求多次前缀和即可。

模板题：智乃酱的静态数组维护问题多项式

#include<bits/stdc++.h>using namespace std;#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\\n'
#define debug(x) cout<<#x<<":"<<x<<endl;typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;
const int cases = 0;LL a[N],ki[N],coef1[N],coef2[N];
int n,m,q;
/*
在数组a的l，r区间加上一个多项式
然后前缀和。
P函数表示求长度为len的数组a，cnt次前缀和
D函数表示求长度为len的数组a，cnt次差分
f函数：a数组表示多项式系数，k表示最高次项
p函数：其实为-f(x+len)
*/
void P(LL a[],int len,int cnt=1){while(cnt--){for(int i=1;i<=len;i++){a[i]+=a[i-1];if(a[i]>=mod) a[i]-=mod;}}
}void D(LL a[],int len,int cnt=1){while(cnt--){for(int i=len;i;i--){a[i]-=a[i-1];if(a[i]<0) a[i]+=mod;}}
}LL f(int x,LL a[],int k){LL res=0;LL base=1;for(int i=k;i>=0;i--){res+=base*a[i]%mod;if(res>=mod) res-=mod;base=base*x%mod;}return res;
}LL g(int x,LL a[],int k,int l,int r){return (mod-f(x+r-l+1,a,k))%mod;
}
void Showball(){cin>>n>>m>>q;for(int i=1;i<=n;i++) cin>>a[i];D(a,n,6);int l,r,k;while(m--){cin>>l>>r>>k;for(int i=0;i<=k;i++){cin>>ki[i];}for(int i=1;i<=10;i++){coef1[i]=f(i,ki,k);coef2[i]=g(i,ki,k,l,r);}D(coef1,10,6);D(coef2,10,6);for(int i=1;i<=10;i++){a[l+i-1]+=coef1[i];if(a[l+i-1]>=mod) a[l+i-1]-=mod;a[r+i]+=coef2[i];if(a[r+i]>=mod) a[r+i]-=mod;}}P(a,n,7);while(q--){int l,r;cin>>l>>r;cout<<(a[r]-a[l-1]+mod)%mod<<endl;}
}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int T=1;if(cases) cin>>T;while(T--)Showball();return 0;
}

高次前缀和

快速的求k次前缀和，当k很大时，就需要用一些高级的东西进行优化，这里用的是卷积进行优化。原理尚不是很明白，先贴一个板子。
智乃酱的前缀和与差分

#include<bits/stdc++.h>
using namespace std;
namespace NTT
{
const long long g = 3;
const long long p = 998244353;
long long wn[35];
long long pow2(long long a, long long b)
{long long res = 1;while (b){if (b & 1) res = res * a % p;a = a * a % p;b >>= 1;}return res;
}
void getwn()
{for (int i = 0; i < 25; i++) wn[i] = pow2(g, (p - 1) / (1LL << i));
}
void ntt(long long *a, int len, int f)
{long long i, j = 0, t, k, w, id;for (i = 1; i < len - 1; i++){for (t = len; j ^= t >>= 1, ~j & t;);if (i < j) swap(a[i], a[j]);}for (i = 1, id = 1; i < len; i <<= 1, id++){t = i << 1;for (j = 0; j < len; j += t){for (k = 0, w = 1; k < i; k++, w = w * wn[id] % p){long long x = a[j + k], y = w * a[j + k + i] % p;a[j + k] = (x + y) % p;a[j + k + i] = (x - y + p) % p;}}}if (f){for (i = 1, j = len - 1; i < j; i++, j--) swap(a[i], a[j]);long long inv = pow2(len, p - 2);for (i = 0; i < len; i++) a[i] = a[i] * inv % p;}
}
void mul(long long *a, long long *b, int l1, int l2)
{int len, i;for (len = 1; len <= l1 + l2; len <<= 1);for (i = l1 + 1; i <= len; i++) a[i] = 0;for (i = l2 + 1; i <= len; i++) b[i] = 0;ntt(a, len, 0); ntt(b, len, 0);for (i = 0; i < len; i++) a[i] = a[i] * b[i] % p;ntt(a, len, 1);
}
};
const int MAXN = 300005;
const long long mod = 998244353;
int n;
long long a[MAXN], inv[MAXN], ki[MAXN], k;
void init(long long n)
{inv[0] = inv[1] = 1;for (long long i = 2; i <= n; i++){inv[i] = ((mod - mod / i) * inv[mod % i]) % mod;}return;
}
void get_ki(long long k, int len)
{k = (k % mod + mod) % mod;ki[0] = 1;for (int i = 1; i < len; ++i){ki[i] = ki[i - 1] * inv[i] % mod * ((k + i - 1) % mod) % mod;}
}
int main()
{NTT::getwn();init(100000);scanf("%d %lld", &n, &k);get_ki(k, n);for (int i = 0; i < n; ++i){scanf("%lld", &a[i]);}NTT::mul(a, ki, n, n);for (int i = 0; i < n; ++i){printf("%lld%c", a[i], i == n - 1 ? '\\n' : ' ');}return 0;
}

高维前缀和 (SOSDP)

对于一般的二维前缀和都是采用容斥原理进行计算的。

s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]

但是对于更高维度的就不太好写了。
这里推荐另外一种写法：

s[i][j]=a[i][j]
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
s[i][j]+=s[i-1][j];for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
s[i][j]+=s[i][j-1];

也就是对每一维分别做前缀和
然后配合状态压缩，我们就可以进行高维前缀和了。操作如下：

 for (int i = 0; i < n; ++i){for (int j = 0; j < (1<<n); ++j){if (j & (1 << i))pre_sum[j] += pre_sum[j ^ (1 << i)];}}

例题：
智乃酱的子集与超集

#include<bits/stdc++.h>using namespace std;#define ff first
#define ss second
#define pb push_back
#define all(u) u.begin(), u.end()
#define endl '\\n'
#define debug(x) cout<<#x<<":"<<x<<endl;typedef pair<int, int> PII;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int N = 1e5 + 10, M = 105;
const int mod = 1e9 + 7;
const int cases = 0;int n,m;
LL pre_sum[1<<20],suf_sum[1<<20];
LL a[M];
void Showball(){cin>>n>>m;LL sum=0;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<(1<<n);i++){LL sum=0;for(int j=0;j<n;j++){if((i>>j)&1) sum^=a[j];}pre_sum[i]=sum;suf_sum[i]=sum;}for(int i=0;i<n;i++){for(int j=0;j<(1<<n);j++){if(j&(1<<i)) pre_sum[j]+=pre_sum[j^(1<<i)];else suf_sum[j]+=suf_sum[j^(1<<i)];}}int k;while(m--){cin>>k;LL p=0;for(int i=0;i<k;i++){int x;cin>>x;p|=(1<<(x-1));}cout<<pre_sum[p]<<" "<<suf_sum[p]<<endl;}}
int main(){ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int T=1;if(cases) cin>>T;while(T--)Showball();return 0;
}

完结撒花~