写在前面的话：以排升序为例

目录

冒泡排序

单趟

循环

优化

快速排序

单趟

递归

优化

不足

冒泡排序

通过重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序错误就把他们交换过来。走访元素的工作是重复地进行，直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

单趟

单趟会通过两两比较的方式将数组中最大的元素排到末尾

	for(int j=0;j<numsSize-1;j++){if(nums[j]>nums[j+1]){Swap(&nums[j],&nums[j+1]);}}

循环

初始：第一趟，是将数组下标从0到numsSize-1的范围中的最大元素放在了numsSize-1的位置上

循环：缩小范围，将数组下标从0到numsSize-2的范围中的最大元素放在numsSize-2的位置上

终止：当范围缩小到一个元素

void Bubble(int* nums,int numsSize)
{for(int i=0;i<numsSize-1;i++){for(int j=0;j<numsSize-1-i;j++){if(nums[j]>nums[j+1]){Swap(&nums[j],&nums[j+1]);}}}
}

优化

优化点在于，当一个升序数组通过冒泡进行排序，时间复杂的是O(N*N)，可以在此种情况优化为O(N)

void Bubble(int* nums,int numsSize)
{for(int i=0;i<numsSize-1;i++){bool exchage=false;for(int j=0;j<numsSize-1;j++){if(nums[j]>nums[j+1]){Swap(&nums[j],&nums[j+1]);exchage=true;}}if(bool==false){break;}}
}

快速排序

我的理解：

快速排序使用递归，在每层的的递归中，只做一件事，那就是将当前范围内的某一个关键字元素（通常选取最左侧元素）放到正确的位置上来

回归，有深层次的递归就要有回归，当某一层递归排序的数组范围小到只有一个及以下的元素个数时，就需要回归结束递归了

单趟

.首先实现将关键元素放到正确的位置上，解释：当一个元素在数组中的位置满足两个条件，我们认为它在正确的位置上

1，在它之前的元素小于它

2，在它之后的元素大于等于它

..这里使用前后指针的方法，关于此方法的理解，我们可以这样看：

将数组划分为两部分：

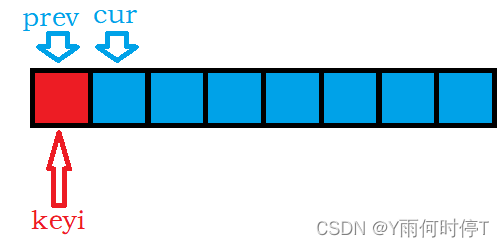
 通过指针cur,prev将蓝色部分调整为蓝色部分中的小于nums[keyi]的元素聚集在前一部分，大于等于nums[keyi]的元素聚集在后一部分：

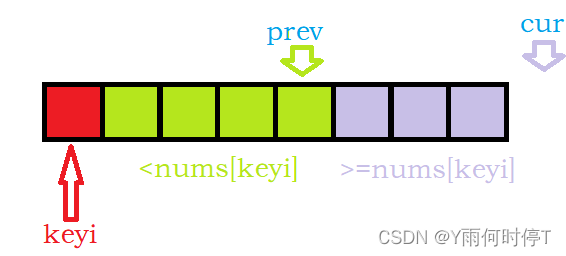
 此时，交换keyi与prev的元素即可使keyi指向的元素来到正确的位置

void QuickSort(int* nums,int left,int right)
{int keyi=left;int prev=left;int cur=prev+1;while(cur<=right){if(nums[cur]<nums[keyi]&&++prev!=cur){Swap(&nums[cur],&nums[prev]);}cur++;}Swap(&nums[prev],&nums[keyi]);
}

递归

递归至回归，即可完成排序（至此快排基本完成，可以完成多数情况下的排序）

void QuickSort(int* nums,int left,int right)
{if(left>=right){return;}int keyi=left;int prev=left;int cur=prev+1;while(cur<=right){if(nums[cur]<nums[keyi]&&++prev!=cur){Swap(&nums[cur],&nums[prev]);}cur++;}Swap(&nums[prev],&nums[keyi]);QuickSort(nums,left,prev-1);QuickSort(nums,prev+1,right);
}

优化

针对部分特殊情况，可以进行相应的优化

一，针对有序数组，当升序数组进入上述快排时，会出现递归层数过深（栈溢出）的问题，应对方法有

1，随机取keyi

2，三数取中

二，当数组长度较小的时候，使用快排是不合适的，在递归层次较深的时候，目标数组长度较小的时候，可以考虑不再继续递归，而是将这一长度较小的数组直接使用插入排序完成排序

给出快排代码：

void* Swap(int* x,int* y)
{int temp=*x;*x=*y;*y=temp;
}int MidNum(int* nums,int left,int right)
{int mid=(left+right)/2;if(nums[left]>nums[right]){if(nums[mid]>nums[right]){return mid;}else if(nums[mid]>nums[left]){return left;}else{return mid;}}else{if(nums[mid]>nums[left]){return mid;}else if(nums[mid]>nums[right]){return right;}else{return mid;}}
}void InsetSort(int* nums,int left,int right)
{for(int i=left;i<right;i++){for(int end=i;end<right;end++){if(nums[end]>nums[end+1]){Swap(&nums[end],&nums[end+1]);}}}
}void QuickSort(int* nums,int left,int right)
{if(left>=right){return;}//三数取中，避免升序数组进入快速排序后栈溢出int mid=MidNum(nums,left,right);Swap(&nums[left],&nums[mid]);int keyi=left;int prev=left;int cur=prev+1;while(cur<=right){if(nums[cur]<nums[keyi]&&++prev!=cur){Swap(&nums[cur],&nums[prev]);}cur++;}Swap(&nums[prev],&nums[keyi]);//当数组长度小到一定范围后，不再通过递归的方式排序，而是通过插入排序将这个长度较短的数组排序if(right-left+1>=13){QuickSort(nums,left,prev-1);QuickSort(nums,prev+1,right);}else{InsetSort(nums,left,right);}
}

不足

依然存在可优化的空间，针对待排序数组中存在大量重复的元素的情况，可以使用三路划分（未掌握，挖个坑）