AS-GCN 论文解读

文章列表

AS-GCN 论文解读

论文名称：Actional-Structural Graph Convolutional Networks for Skeleton-based Action Recognition
论文下载：https://arxiv.org/pdf/1904.12659.pdf
论文代码：https://github.com/GeneZC/ASGCN

论文：基于骨骼动作识别的动作-结构图卷积网络

摘要

骨骼数据动作识别近年来在计算机视觉领域引起了广泛关注。先前的研究大多基于固定的骨骼图，仅捕捉关节之间的局部物理依赖关系，可能会忽略隐含的关节相关性。

为了捕捉更丰富的依赖关系，我们引入了编码器-解码器结构，称为 A-link 推断模块，直接从动作中捕捉动作特定的潜在依赖关系，即动作链接。

我们还扩展了现有的骨骼图以表示更高阶的依赖关系，即结构链接。

将这两种链接组合成一个通用的骨骼图，我们进一步提出了动作-结构图卷积网络（AS-GCN），它将动作-结构图卷积和时间卷积堆叠成一个基本构建块，学习用于动作识别的空间和时间特征。

同时，在识别头部并行增加了未来姿态预测头部，通过自监督帮助捕捉更详细的动作模式。

我们在两个骨骼数据集 NTURGB+D 和 Kinetics 上验证了 AS-GCN 的性能，在与现有最先进方法相比，AS-GCN 取得了一致的更大改进。作为副功能，AS-GCN 展示了精确的未来姿态预测结果。

引入

ST-GCN 虽然提取了通过骨骼直接连接的关节的特征，但结构上远离的关节，可能涵盖动作的关键模式，往往被忽视。例如，走路时，手和脚是紧密相关的。虽然 ST-GCN 试图用分层 GCNs 聚合更大范围的特征，但在长扩散过程中，节点特征可能会减弱。

下图展示了 AS-GCN 模型的特征，其中我们学习了活动链接并扩展了用于动作识别的结构链接。特征响应表明，与 ST-GCN 相比，我们可以捕获更多的全局关节信息，ST-GCN 仅使用骨架图来建模局部关系。
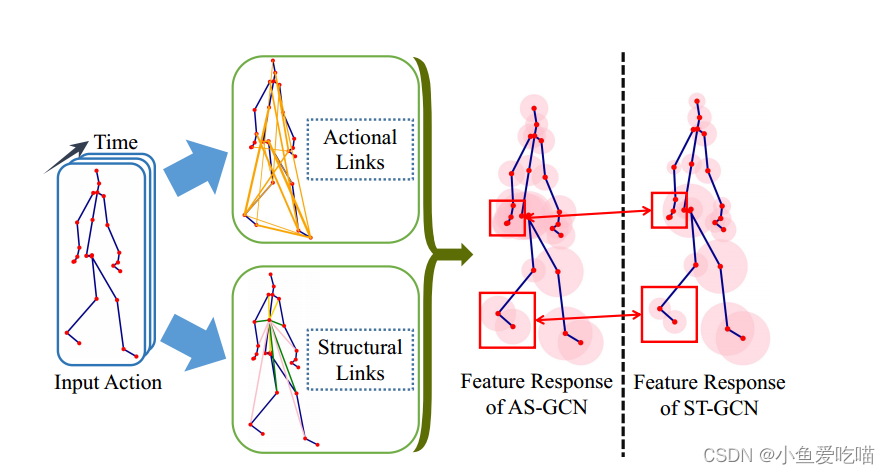
AS-GCN 论文解读
上图为使用广义骨架图进行特征学习示意图。活动链接和结构链接捕获关节之间的依赖关系。对于“行走”这个动作，动作链接表示手和脚是相关的。右侧主体上的半透明圆为用于识别的关节特征图，其面积为响应幅度。与 ST-GCN 相比，AS-GCN 得到了协同运动关节的响应(红框)。

直觉上，“行走”这个动作，手和腿的联系比较大，在 ST-GCN 中，手和腿距离较远，联系很小。而在 AS-GCN 中，手和腿的联系明显大很多，这从图上的红色圆圈大小也可以看出来。这就是 AS-GCN 改进的成果。

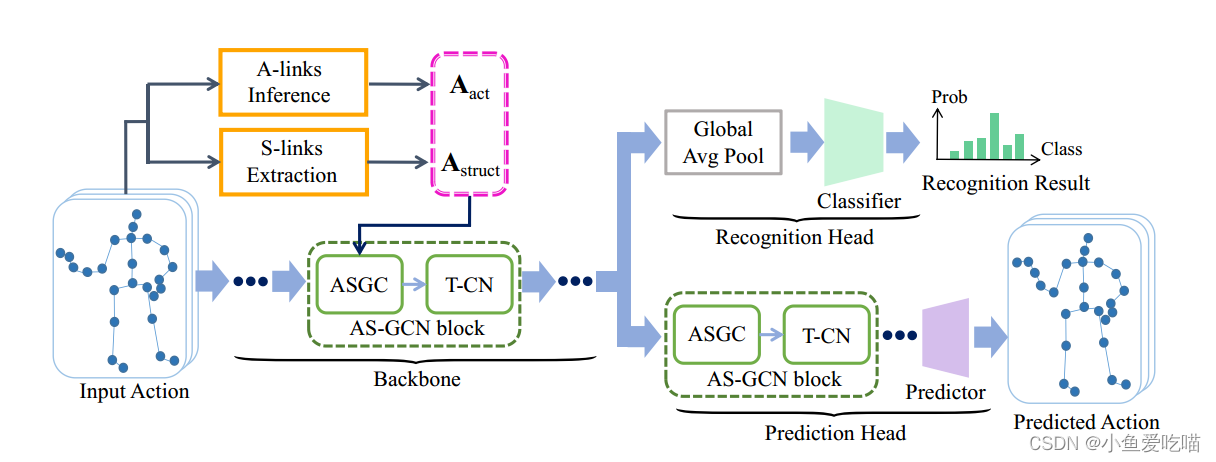
AS-GCN 论文解读
提出的 AS-GCN 的流程如上图所示。推断出的动作链接和扩展的结构链接被输入到 AS-GCN 块中以学习空间特征。最后一个 AS-GCN 块连接到两个并行分支，即识别头和预测头，两者同时进行训练。

主要贡献

我们提出了 A-link 推断模块 (AIM) 来推断动作链接，捕捉动作特定的潜在依赖关系。将动作链接与结构链接组合成通用骨架图；
我们提出了动作-结构图卷积网络 (AS-GCN)，以基于多个图的方式提取有用的空间和时间信息；
我们引入了一个额外的未来姿态预测头部来预测未来姿态，通过捕捉更详细的动作模式，同时也提高了识别性能；
在两个大规模数据集上，AS-GCN 超越了几种最先进的方法；作为副功能，AS-GCN 还能够精确地预测未来姿态。

与之前的任何方法不同，我们通过自适应地从数据中学习图形来捕捉关于动作的有用非局部信息。

背景材料

1. 符号

我们将骨架图视为 $G(V,E)\\mathcal G(V, E)$ ，其中 $V$ 是 $n$ 个身体关节的集合， $E$ 是 $m$ 个骨骼的集合。设 $A∈{0,1}n×n\\mathbf A∈\\{0,1\\}^{n×n}$ 为骨架图的邻矩阵，其中，如果第 $i$ 个和第 $j$ 个关节连通， $Ai,j=1\\mathbf A_{i,j} = 1$ ，否则为0。 $A\\mathbf A$ 完整地描述了框架结构。设 $D∈Rn×nD∈\\mathbb R^{n×n}$ 为对角度矩阵，其中 $Di,i=∑jAi,jD_{i,i} = \\sum_j \\mathbf A_{i,j}$ 。

为了获取更精确的位置信息，我们将一个根节点及其相邻节点分为三个集合，包括1)根节点本身，2)向心组，它比根更接近身体重心，3)离心组， $A\\mathbf A$ 相应地分为 $A(根)\\mathbf A^{(根)}$ ， $A(向心)\\mathbf A^{(向心)}$ 和 $A(离心)\\mathbf A^{(离心)}$ 。我们将划分组表示为 $P\\mathcal P$ ={根，向心，离心}。

注意 $∑p∈PA(P)=A\\sum_{p∈\\mathcal P} \\mathbf A^{(P)} = \\mathbf A$ ，设 $X∈Rn×3×T\\mathcal X∈\\mathbb R^{n×3×T}$ 为跨 $T$ 帧的三维关节位置。设 $Xt=X:,:,t∈Rn×3\\mathbf X_t = \\mathcal X_{:,:,t}∈\\mathbb R^{n×3}$ 为第 $t$ 帧上的三维关节位置，它在 $X\\mathcal X$ 的最后一个维度上对第 $t$ 帧进行切片。设 $xit=Xi,:,t∈Rd\\mathbf x^t_i=\\mathcal X_{i,:,t}∈\\mathbb R^d$ 是第 $i$ 个关节在第 $t$ 帧中的位置。（这里 $d = 3$ ，因为是三维关节位置）

2. ST-GCN

时空 GCN (ST-GCN)[29]由一系列 ST-GCN 块组成。每个块包含一个空间图卷积和一个时间卷积，交替提取空间和时间特征。最后一个 ST-GCN 块连接到一个全连接分类器以生成最终的预测。

ST-GCN 的关键部分是空间图卷积运算，它为每个关节引入了相邻特征的加权平均。设 $Xin∈Rn×din\\mathbf X_{in}∈\\mathbb R^{ n×d_{in}}$ 为一帧内所有关节的输入特征，其中 $d_{in}$ 为输入特征维数， $Xout∈Rn×dout\\mathbf X_{out}∈\\mathbb R^{n×d_{out}}$ 为空间图卷积得到的输出特征，其中 $d_{out}$ 为输出特征维数。空间图卷积为 $Xout=∑p∈PMst(p)∘A(p)~XinWst(p)(1)\\mathbf X_{out} = \\sum_{p∈\\mathcal P} \\mathbf M_{st}^{(p)} \\circ \\widetilde{ \\mathbf A^{(p)} } \\mathbf X_{in} \\mathbf W_{st}^{(p)}\\tag{1}$ 其中 $A(p)~=D(p)−12A(p)D(p)−12∈Rn×n\\widetilde{ \\mathbf A^{(p)} } = \\mathbf {D^{(p)}}^{-\\frac{1}{2}} \\mathbf A^{(p)} \\mathbf {D^{(p)}}^{-\\frac{1}{2}} ∈\\mathbb R^{n×n}$ 是每个分区组的归一化邻矩阵， $∘\\circ$ 表示 $H a d ama r d$ 积， $Mst(p)∈Rn×nM^{(p)}_{st}∈\\mathbb R^{n×n}$ 和 $Wst(p)∈Rn×doutW^{(p)}_{st}∈\\mathbb R^{n×d_{out}}$ 是每个分区组的可训练权值，分别用于捕获边缘权值和特征重要性。

ST-GCN 将感受野内的点分为三种：源点、近心点和远心点。这里 $p$ 就是三种里面其中一种。 $Xin\\mathbf X_{in}$ 是输入的数据， $A(p)~\\widetilde{ \\mathbf A^{(p)} }$ 是经过标准化之后的邻接矩阵， $Wst(p)\\mathbf W_{st}^{(p)}$ 是网络的权重， $Mst(p)\\mathbf M_{st}^{(p)}$ 是有关注意力机制的权重。

Actional-Structural GCN

广义图，称为动作-结构图，定义为 $Gg(V,Eg)\\mathcal G_g(V, E_g)$ ，其中 $V$ 是关节的原始集合， $E_g$ 是广义连接的集合。 $E_g$ 中有两种类型的链接：

结构链接(S-links)，显式地从主体结构派生出来；
活动链接(A-links)，直接从骨架数据推断出来。

参见下图这两种类型的说明。

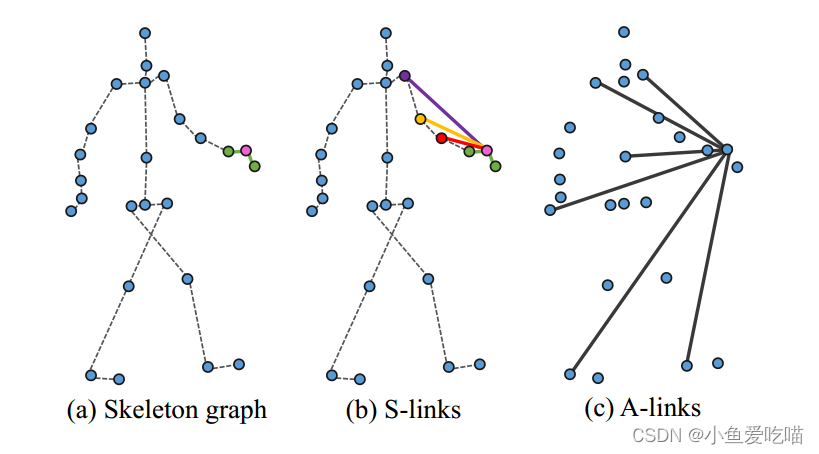
AS-GCN 论文解读

上图是骨架图的一个例子，用于行走的 S-links 和 A-links。在每个图中，从“左手”到它的邻居的链接用实线显示。（a）骨架连接有限的邻近范围；（b）S-links，使“左手”能连接到整个手臂；（c） A-links，捕捉远程具体行动关系。

图（a）的左手中紫色关节是源节点，在 ST-GCN 中只会考虑与之直接相连的绿色节点。图（c）是 A-links 的示意图，源点和身体部位任何点都有可能有关系，具体有什么关系，要网络自己去识别（训练）。图（b）是 S-links 的示意图，有点像 ST-GCN 中的结构，只不过这里会参考与源点相近的 L 个节点，这里 L>1，也就是说参考的节点多了。

1. A-links

人类的许多动作需要相距很远的关节才能协同移动，导致关节之间存在非物理依赖性。

为了捕获各种操作的相应依赖关系，我们引入了活动激活的链接(A-links)，它们可能存在于任意一对关节之间。

为了从动作中自动推断 A-links，我们开发了一个可训练的 A-links 推断模块(AIM)，它由一个编码器和一个解码器组成。

编码器通过在关节和链接之间迭代传播信息来生成 A-links，以学习链接特征；
解码器基于推断出的 A-links 预测未来的关节位置；

我们使用 AIM 来预热（warm-up）A-links，在训练过程中进一步调整，参见下图。

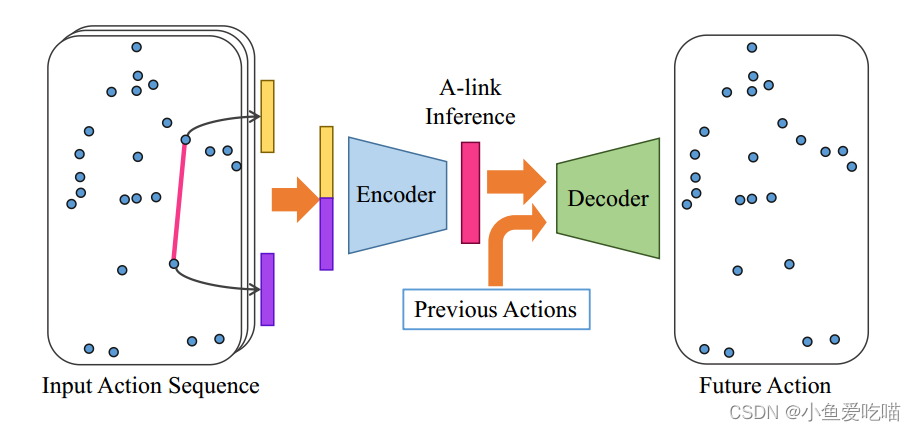
AS-GCN 论文解读
A-links 推理模块(AIM)。为了推断两个关节之间的 A-links，将关节特征连接起来，并将其输入组成 AIM 的编码器-解码器。编码器产生推断的 A-links，解码器根据 A-links 和之前的动作生成未来的姿势。

整篇文章最难的就是 A-links 的具体实现过程了，整个结构图如图，源点和其他点的连接都会通过一个编码器和解码器，输出的结果是预测的关节位置。

1.1 编码器

编码器的功能是在给定三维关节位置的情况下估计 A-links 的状态，即 $A=encode(X)∈[0,1]n×n×C(2)\\mathcal A = encode(\\mathcal X)∈[0,1]^{n×n×C} \\tag{2}$ 其中 $C$ 是 A-links 类型的数量。每个元素 $A_{i,j,c}$ 表示第 $i, j$ 个关节与第 $c$ 种类型链接的概率。

在实际情况中，不同种类的 A-links 可能具有不同的物理属性和运动约束，因此选择不同的链接方式会影响到人的运动表现等方面。

设计映射 $e n co d e (\cdot)$ 的基本思想是首先从三维关节位置精确链接特征，然后将链接特征转换为链接概率。

后一步很好解决，就是加入 $S o f t ma x$ 层， $\\ softmax$ 近似分类；
主要是提取连接特征，整个提取的过程就是循环迭代。

为了精确的链接特征，我们在关节和链接之间交替传播信息。
设 $xi=vec(Xi,:,:)∈RdT\\mathbf x_i = vec (\\mathcal X_i,:,:)∈\\mathbb R^{dT}$ 是第 $i$ 个关节在所有 $T$ 帧上的特征的向量表示。我们初始化关节特征 $pi(0)=xi\\mathbf p^{(0)}_i = \\mathbf x_i$ 。

$p_i$ 和 $p_j$ 分别是第 $i$ 个节点和第 $j$ 个节点在所有 $T$ 帧上的关节特征（特征的向量表示）， $f_v$ 和 $f_e$ 分别是对关节点和边的多层感知机（MLP）， $Q_{i,j}$ 是第 $i$ 个节点和第 $j$ 个节点的连接（link）。

在第 $k$ 次迭代中，我们在关节和链接之间来回传播信息， $linkfeatures:Qi,j(k+1)=fe(k)(fv(k)(pi(k))⊕(fv(k)(pj(k)))jointfeatures:pi(k+1)=F(Qi,:(k+1))⊕pi(k)\\begin{aligned} &link \\ features: \\mathbf Q^{(k+1)}_{i,j} = f^{(k)}_e (f^{(k)}_v (\\mathbf p^{(k)}_i)⊕(f^{(k)}_v (\\mathbf p^{(k)}_j))\\\\ &joint \\ features:\\mathbf p^{(k+1)}_i = \\mathcal F (\\mathbf Q^{(k+1)}_{i,:})⊕\\mathbf p^{(k)}_i\\\\ \\end{aligned}$

其中 $f_v(·)$ 和 $f_e(·)$ 都是多层感知器， $\oplus$ 是向量拼接， $F(⋅)\\mathcal F(·)$ 是聚合链接特征并获得关节特征的操作，比如求平均和元素最大化。

对于我们要计算的第 $i$ 个关节点，和要与之建立联系的第 $j$ 个关节点，先通过 $f_v$ 分别提取关节特征，再通过向量连接（ $\oplus$ ）拼接到一起，最后通过 $f_e$ 得到 $i$ 节点和 $j$ 节点的连接特征。这一步要计算所有 $i$ 节点和其他节点之间的连接特征。下一步 $F(⋅)\\mathcal F(·)$ 函数是取均值或者元素最大值， $F(Qi,:)\\mathcal F (\\mathbf Q_{i,:})$ 是指取所有与 $i$ 节点有联系的连接特征的均值或者最大值。然后再与原来的 $p_i$ 按向量连接得出的结果作为下一次迭代的 $p_i$ 。

在传播 $K$ 次之后，编码器输出链接概率为 $Ai,j,:=softmax(Qi,j(K)+rτ)∈RC(3)\\mathcal A_{i,j,:} = softmax \\left(\\frac {\\mathbf Q^{(K)}_{i,j} + \\mathbf r}{τ} \\right)∈\\mathbb R^C \\tag{3}$ 其中 $r\\mathbf r$ 为随机向量，其元素为从 $G u mb e l (0, 1)$ 分布采样的 $i . i . d .$ ， $τ$ 控制 $Ai,j,:\\mathcal A_{i,j,:}$ 的离散化。这里我们设 $τ = 0.5$ 。我们用 $\\ softmax$ 近似分类形式得到了连接概率 $Ai,j,:\\mathcal A_{i,j,:}$ 。

编码过程中，输入的是关节数据，输出的是每种类型的概率值。

1.2 解码器

解码器的功能，以预测未来的三维关节位置为条件，由编码器和以前的姿势推断 A-links，即 $Xt+1=decode(Xt,...,X1,A)∈Rn×3\\mathbf X_{t+1} = decode( \\mathbf X_t, ... ,\\mathbf X_1, \\mathcal A) ∈\\mathbb R^{n×3}$ 其中 $Xt\\mathbf X_t$ 是第 $t$ 帧的三维关节位置。其基本思想是首先基于 A-links 提取关节特征，然后将关节特征转换为未来的关节位置。

设 $xit∈Rd\\mathbf x_i^t∈\\mathbb R^d$ 是第 $i$ 个关节在第 $t$ 帧中的特征。映射 $d eco d e (\cdot)$ 的工作方式为

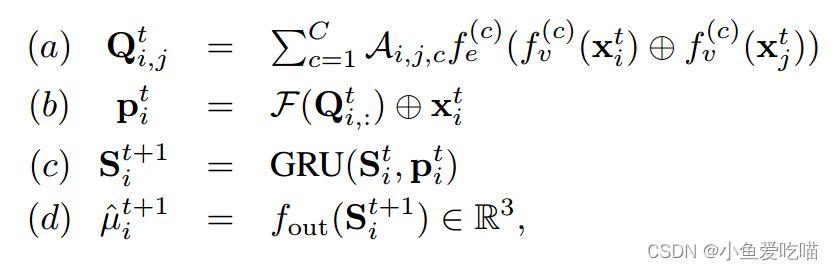
AS-GCN 论文解读
其中 $fv(c)(⋅)f^{(c)}_v(·)$ ， $fe(c)(⋅)f^{(c)}_e(·)$ 和 $f_{out}(·)$ 为 MLPs。

用 GRU 更新关节特征是因为这里输入的是序列，GRU 和 LSTM 类似都是处理序列的，只不过 GRU 参数较少。

步骤（a）通过对链接概率 $A_{i,j,:}$ 进行加权平均生成链接特征，得到的是 $t$ 帧的连接特征，注意这里不是所有帧。
步骤（b）对链接特征进行聚合，得到相应的关节特征；
步骤（c）使用门控循环单元(GRU)更新关节特征；
步骤（d）预测未来关节位置的平均值。

这里要满足一个条件： $∑c=1CAi,j,c=1\\sum^C_{c=1} \\mathcal A_{i,j,c} =1$ ，也就是每种类型的概率和为1。但是注意这里 $c$ 的取值不包括0。其实这样设置就增加了复杂性，虽然 A-links 是在所有节点寻找连接的类型，但是并不是所有节点都有很强的联系，所以这里相当于加了一个0类型，也就是没有连接。最后是： $\\mathcal A_{i,j,0} + \\sum^C_{c=1} \\mathcal A_{i,j,c} =1$ ，并且将0类型的概率设置大一点。

最后，我们从服从以公式（d）作为均值的高斯分布中对未来关节位置 $x^it+1∈R3\\hat {\\mathbf x}^{t+1}_i∈\\mathbb R^3$ 进行抽样，即 $x^it+1∼N(µ^it+1，σ2I)\\hat {\\mathbf x}^{t+1}_i∼ \\mathcal N( \\hat{µ}^{t+1}_i， σ^2 \\mathbf I)$ ，其中 $σ^2$ 表示方差， $I\\mathbf I$ 是单位矩阵。

我们预先训练 AIM 几个阶段来热身 A-links。数学上，AIM 的代价函数为
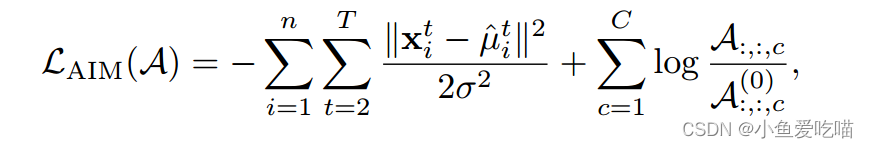
AS-GCN 论文解读
其中， $A:,:,c(0)\\mathcal A^{(0)}_{:,:,c}$ 是 $A\\mathcal A$ 的先验。在实验中，我们发现当 $p(A)p(\\mathcal A)$ 促进稀疏性时，性能提高。背后的直觉是，太多的链接会捕获无用的依赖关系，从而混淆动作模式学习；而在(a)中，我们保证 $∑c=1CAi,j,c=1\\sum^C_{c=1} \\mathcal A_{i,j,c} =1$ 。

由于概率1分配给 $C$ 链路类型，当 $C$ 较小时，很难促进稀疏性。为了控制稀疏度，我们引入了一个大概率的幽灵链接，表示两个关节没有通过任何 A-link。幽灵链接仍然确保概率之和为1；即 $\\mathcal A_{i,j,0} + \\sum^C_{c=1} \\mathcal A_{i,j,c} =1$ ，其中 $A_{i,j,0}$ 为隔离概率。

这里我们设置了 $c = 1, 2,\cdot\cdot\cdot\cdot, C$ 时的先验 $A:,:,0(0)=P0\\mathcal A^{(0)}_{:,:,0} = P_0$ 和 $A:,:,c(0)=P0/C\\mathcal A^{(0)}_{:,:,c} = P_0/ C$ 。在 AIM 的训练中，我们只更新 A-links $A_{i,j,c}$ 的概率，其中 $c = 1,\cdot\cdot\cdot\cdot, C$ 。

我们对多个样本累积 $LAIM\\mathcal L_{AIM}$ 并将其最小化，以获得一个 warmed-up $A\\mathcal A$ 。令 $Aact(c)=A:,:,c∈[0,1]n×n\\mathbf A^{(c)}_{act} = \\mathcal A_{:,:,c} ∈ [0,1]^{n×n}$ 表示第 $c$ 类连接概率，表示第 $c$ 类行动图的拓扑结构。我们定义了行动图卷积（AGC），它利用 A-links 来捕捉关节之间的行动性依赖关系。在 AGC 中，我们使用 $A^act(c)\\hat A^{(c)}_{act}$ 作为图卷积核，其中 $A^act(c)=Dact(c)−1Aact(c)\\hat {\\mathbf A}^{(c)}_{act} = { \\mathbf D^{(c)}_{act} }^{−1} \\mathbf A^{(c)}_{act}$ 。给定输入 $Xin\\mathbf X_{in}$ ，AGC 是
$Xact=AGC(Xin)=∑c=1CA^act(c)XinWact(c)∈Rn×dout(4)\\begin{aligned} \\mathbf X_{act} & = AGC(\\mathbf X_{in}) \\tag{4} \\\\ &=\\sum^C_{c=1} \\hat { \\mathbf A}^{(c)}_{act} \\mathbf X_{in} \\mathbf W^{(c)}_{act} ∈ \\mathbb R^{n × d_{out}} \\end{aligned}$
其中 $Wact(c)W^{(c)}_{act}$ 行为是捕获特征重要性的可训练权重。请注意，我们在预训练过程中使用 AIM 来热身 A-links；在动作识别和姿态预测训练过程中，只对 AIM 编码器进行前向传递，进一步优化 A-links。

2. S-links

正如(1)所示， $A(p)~Xin\\widetilde{ \\mathbf A^{(p)} } \\mathbf X_{in}$ 在骨架图中聚合1跳邻居信息；也就是说，ST-GCN 的每一层都只扩散局部范围内的信息。为了获得长距离链接，我们使用 $A\\mathbf A$ 的高阶多项式，表示 S-links。这里我们使用 $A^L\\hat {\\mathbf A}^L$ 作为图卷积核，其中 $A^=D−1A\\hat {\\mathbf A} = \\mathbf D^{-1} \\mathbf A$ 是图转换矩阵， $L$ 是多项式阶数。 $A^\\hat {\\mathbf A}$ 引入度归一化以避免星等爆炸，具有概率直觉[1,4]。利用 $L$ 阶多项式，我们定义了结构图卷积(SGC)，它可以直接到达 $L$ 跳邻居来增加接收域。

S-links 其实很好理解，因为 ST-GCN 只考虑源节点直接连接的节点，也就是说只有1跳，这篇文章是设置 L 跳，打个比方就是如果源节点在手上，那么 S-links 就能将整只手连接起来。

SGC 的公式为：

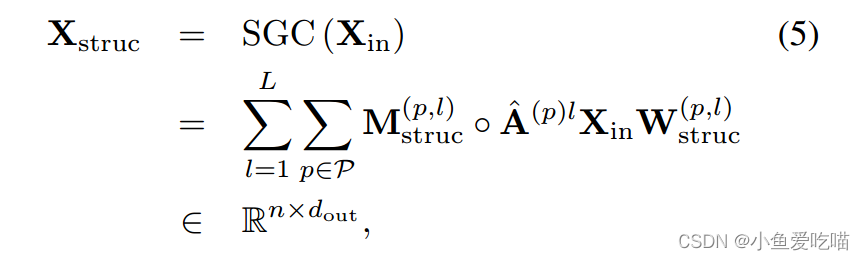
AS-GCN 论文解读

其中 $l$ 为多项式阶， $A^(p)\\hat{\\mathbf A}^{(p)}$ 为 $p$ 分图的图转移矩阵， $Mstruc(p,l)∈Rn×n\\mathbf M^{(p,l)}_{struc}∈\\mathbb R^{n×n}$ 和 $Wstruc(p,l)∈Rn×dstruc\\mathbf W^{(p,l)}_{struc}∈\\mathbb R^{n×d_{struc}}$ 为可训练权值，用于捕获边权值和特征重要性；即权重越大，对应的特征越重要。为每个多项式阶和每个单独的分离图引入权重。

注意，通过度归一化，图转换矩阵 $A^(p)\\hat{\\mathbf A}^{(p)}$ 为边权提供了很好的初始化，这稳定了 $Mstruc(p,l)\\mathbf M^{(p,l)}_{struc}$ 结构的学习。当 $L = 1$ 时，SGC 退化为原来的空间图卷积运算。对于 $L > 1$ ，SGC 的作用类似于切比雪夫滤波器，能够近似图谱域[2]中设计的卷积。

3. 动作结构图卷积块

为了从整体上捕捉任意关节间的运动和结构特征，我们将 AGC 和 SGC 结合起来，建立了运动-结构图卷积(AS-GC)。

在(4)和(5)中，我们分别从每个时间戳中的 AGC 和 SGC 中获得关节特征。我们使用两者的凸组合作为 AS-GC 的响应。在数学上，AS-GC 操作被表述为
$Xout=ASGC(Xin)=Xstruc+λXact∈Rn×dout\\begin{aligned} \\mathbf X_{out} &= ASGC (\\mathbf X_{in}) \\\\ &= \\mathbf X_{struc} + λ \\mathbf X_{act}∈ \\mathbb R^{n×d_{out}} \\end{aligned}$
其中 $λ$ 是一个超参数，它权衡了结构特征和动作特征之间的重要性。AS-GC 后可以进一步引入非线性激活函数，如 $R e LU (\cdot)$ 。

还需要注意的就是，A-links 和 S-links 是相互独立的，因为 A-links 只是考虑关节点坐标，没有考虑他们物理上有没有连接，而 S-links 只是考虑物理上相连的关节点。所以他们满足线性关系，他们的贡献相互不影响。

定理1

动作-结构图卷积是一种有效的线性运算；即当 $Y1=ASGC(X1)\\mathbf Y_1 = ASGC (\\mathbf X_1)$ ， $Y2=ASGC(X2)\\mathbf Y_2 = ASGC (\\mathbf X_2)$ 那么， $\\mathbf Y_1 + b \\mathbf Y_2 = ASGC (a \\mathbf X_1 + b \\mathbf X_2)$ ， $\\mathbb R$ 。

线性特性确保 ASGC 从结构和作用两个方面有效地保存信息；例如，当动作方面的响应较强时，可以通过 ASGC 有效地反映出来。

为了捕获帧间动作特征，我们沿时间轴使用一层时间卷积(T-CN)，它独立提取每个关节的时间特征，但共享每个关节的权重。由于 ASGC 和 T-CN 分别学习空间和时间特征，我们将这两层连接为一个动作-结构图卷积块(AS-GCN 块)，以从各种动作中提取时间特征；参见下图：

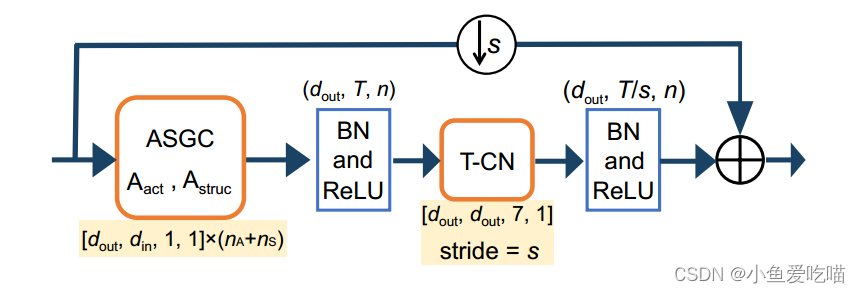
AS-GCN 论文解读
AS-GCN 块由 ASGC、T-CN、批处理归一化(batch normalization, BN)、ReLU 和残差块等操作组成。数据的维度在 BN 和 ReLU 块之上，网络参数的维度在ASGC 和 T-CN 下。

请注意，ASGC 是一个仅提取空间信息的单一操作，而 AS-GCN 块包括一系列同时提取空间和时间信息的操作。

4. AS-GCN 的多任务处理

4.1 骨干网络

我们将一系列 AS-GCN 块堆叠成骨干网，称为 AS-GCN；AS-GCN 的骨干网包括9个 AS-GCN 块，每个块的特征维数见下图：

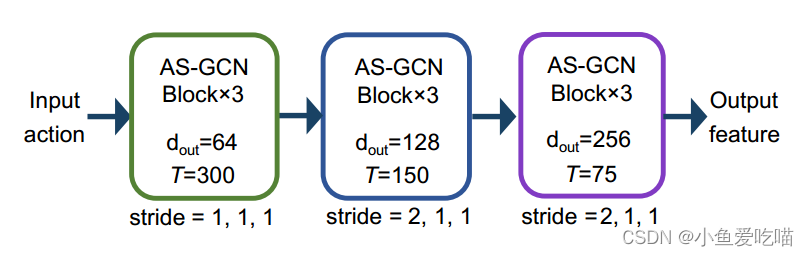
AS-GCN 论文解读
经过多个时空特征聚合后，AS-GCN 提取出跨时间的高级语义信息。

4.2 动作识别头部网络

为了对动作进行分类，我们根据骨干网构造了一个识别头。在骨干网输出的特征图的关节维和时间维上进行全局平均池化，得到特征向量，最后将特征向量输入softmax分类器，得到预测的类标签 $y^\\hat {\\mathbf y}$ 。动作识别的损失函数是标准交叉熵损失 $Lrecog=−yTlog(y^)\\mathcal L_{recog} = - \\mathbf y^T log(\\hat{ \\mathbf y})$ 其中 $y\\mathbf y$ 是动作的基本真理标签。

4.3 未来姿态预测头

以往关于骨架数据分析的工作大多集中在分类任务上。这里我们还考虑了姿态预测；也就是说，使用 AS-GCN 来预测基于骨骼的历史动作给出的未来3D关节位置。

为了预测未来的姿态，我们构建了一个预测模块，然后是骨干网。我们使用几个 AS-GCN 块对从历史数据中提取的高级特征图进行解码，得到预测的未来三维关节位置 $X^∈Rn×3×T′\\hat{ \\mathcal X}∈ \\mathbb R^{n×3×T'}$ ；AS-GCN 未来预测头参见下图：

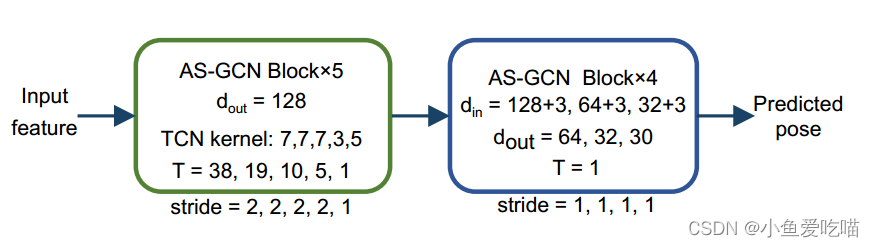
AS-GCN 论文解读
未来预测的损失函数是标准的 $ℓ2\\ell _2$ 损失 $Lpredict=1ndT′∑i=1nd∑t=1T′∥X^i,:,t−Xi,:,t∥22(6)\\mathcal L_{predict} = \\frac{1}{ndT'} \\sum^{nd}_{i=1} \\sum^{T'}_{t=1} \\left\\| \\hat{\\mathcal X}_{i,:,t} - \\mathcal X_{i,:,t} \\right\\| ^2_2 \\tag{6}$

4.4 联合模型

在实践中，将识别头和未来预测头结合起来训练，识别性能得到了提高。背后的直觉是，未来预测模块促进了自我监督，避免了识别上的过拟合。

实验

我们将基于骨骼的动作识别任务上的 AS-GCN 与 NTU-RGB+D 和 Kinetics 数据集上的最先进方法进行了比较。

论文理解参考：【骨骼行为识别】AS-GCN论文理解

AS-GCN 论文解读

论文：基于骨骼动作识别的动作-结构图卷积网络

摘要

引入

主要贡献