力扣70爬楼梯:思路分析+优化思路+代码实现+补充思考

文章目录
- 第一部分:题目描述
- 第二部分:思路分析
-
- 2.1 初步分析
- 2.2 问题描述
- 2.3 优化思路
- 第三部分:代码实现
- 第四部分:补充思考
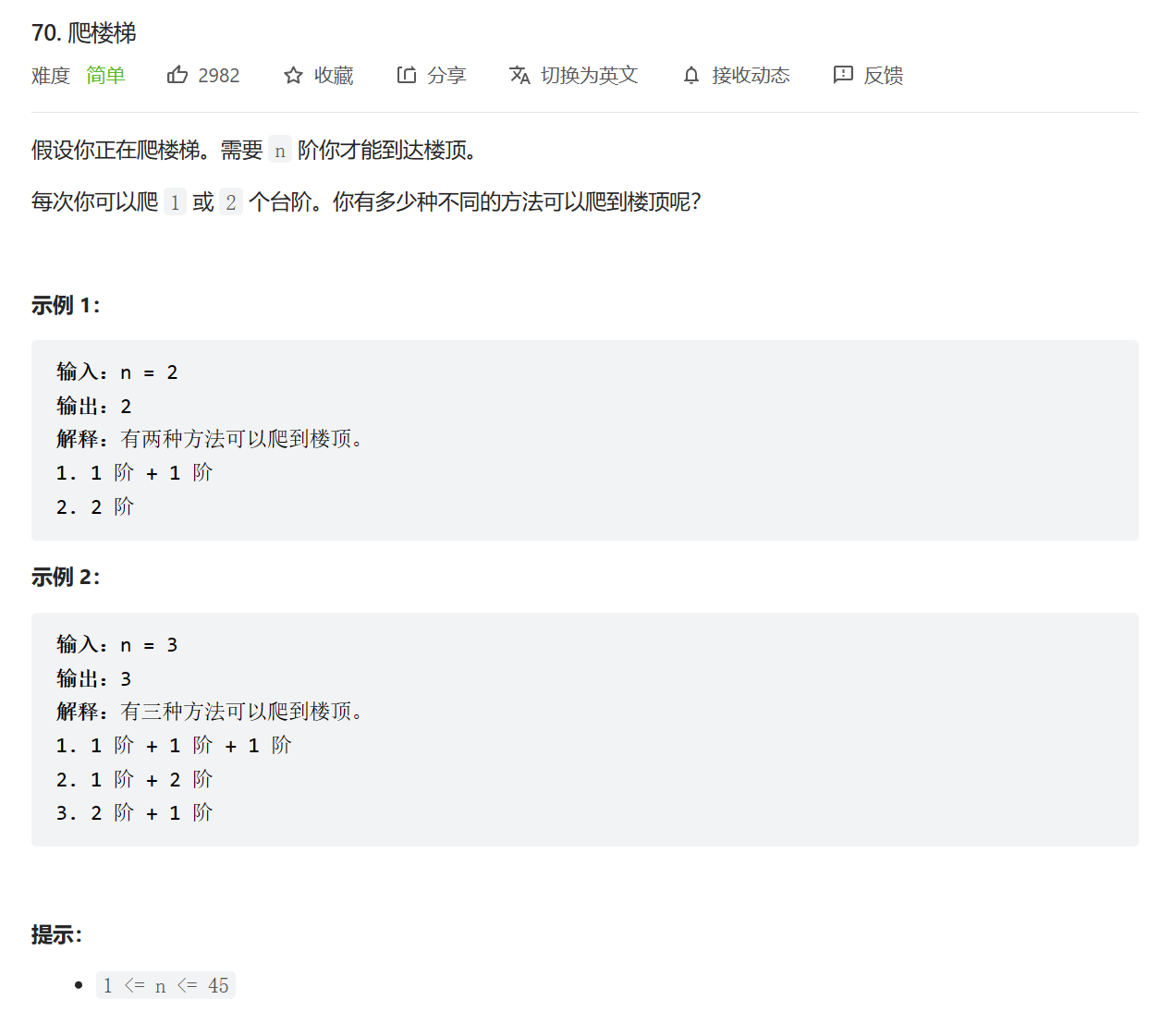
第一部分:题目描述
🏠 链接:70. 爬楼梯 - 力扣(LeetCode)
⭐ 难度:简单
第二部分:思路分析
2.1 初步分析
| n | 跳法 | 规律 |
|---|---|---|
| 1 | (1) | |
| 2 | (1,1) (2) | |
| 3 | (1,1,1) (1,2) (2,1) | 最后一跳,跳一个台阶的,基于f(2) 最后一跳,跳两个台阶的,基于f(1) |
| 4 | (1,1,1,1) (1,2,1) (2,1,1) (1,1,2) (2,2) |
最后一跳,跳一个台阶的,基于f(3) 最后一跳,跳两个台阶的,基于f(2) |
| 5 | … | … |
其实际上,我们只需要分析青蛙的最后一跳:
- 如果最后一跳是跳一个台阶,那么在这之前跳过的 n-1 个台阶总共的跳法有
f(n-1)种。 - 如果最后一跳是跳两个台阶,那么在这之前跳过的 n-2 个台阶总共的跳法有
f(n-2)种。
那么我们可以得到一个青蛙的斐波拉契数列公式:f(n) = f(n-1) + f(n-2)
所以java代码就很简单了:
class Solution {public int climbStairs(int n) {if (n == 1) {// 如果台阶为1,则调到台阶为1的跳法有1种return 1;} else if (n == 2) {// 如果台阶为2,则调到台阶为2的跳法有2种return 2;} else {// 否则调到台阶为n的跳法为:跳到台阶为n-1的跳法总数 + 跳到台阶为n-2的跳法总数return climbStairs(n - 1) + climbStairs(n - 2);}}
}
2.2 问题描述
遗憾的是,使用普通的斐波拉契递归方法会出现如下错误:
关于原因,是由于上述代码存在很多重复的计算导致了超时,例如求 f(5)f(5)f(5) 递归分解过程:

可以看到(颜色相同的是重复的):
- f(3)f(3)f(3) 重复了 2 次
- f(2)f(2)f(2) 重复了 3 次
- f(1)f(1)f(1) 重复了 5 次
- f(0)f(0)f(0) 重复了 3 次
随着 nnn 的增大,重复次数非常可观,如何优化呢?
2.3 优化思路
Memoization 记忆法(也称备忘录)是一种优化技术,通过存储函数调用结果(通常比较昂贵),当再次出现相同的输入(子问题)时,就能实现加速效果。
我们需要做的,就是提前建立一个 n+2 大小的数组cache,每次递前先查询 cache[x] 是否已经缓存了 f(x) 的值:
- 如果没有那么就把这个 f(x) 的值放入到 cache[x] 中,下次如果再遇到要计算 f(x) 时先去数组中cache[x]寻找是否已经缓存。
- 如果有,就直接从缓存数组中拿到 cache[x] 作为 f(x) 的值,避免重复计算。
第三部分:代码实现
class Solution {public int climbStairs(int n) {// 建立缓存数组,大小为 n+2 是避免当n为1时存在cache[2] = 2的赋值数组越界异常。/// 我们规定 台阶数为 x 时,跳法f(x) 对应 cache[x]int[] cache = new int[n + 2];// 初始化:当台阶数为1时,跳法为1cache[1] = 1;// 初始化:当台阶数为2时,跳法为2cache[2] = 2;return recursion(cache, n);}public int recursion(int[] cache, int x) {// 先计算是否已经对台阶数为x的跳法f(x)值进行了缓存// 如果缓存了,则直接返回 cache[x] 的值if (cache[x] != 0) {return cache[x];}// 走到这里说明If不成立,没有缓存,则使用斐波拉契公式递归计算 f(x) 的值int cacheValue = recursion(cache, x - 1) + recursion(cache, x - 2);// 递归计算完成,则在数组中进行缓存cache[x] = cacheValue;// 返回 跳法种数 f(x)return cacheValue;}
}
第四部分:补充思考
- 改进后的时间复杂度为 O(n)O(n)O(n)。
- 记忆法是动态规划的一种情况,强调的是自顶向下的解决。
- 记忆法的本质是空间换时间


