背包问题，简单概括就是如何在有限的容量下，装下最大价值的东西。这个问题听起来像是一个简单的选择题，但实际应用中可能是一个大写的“南”。这篇文章主要讲了几种常见的背包问题，包括01背包、完全背包、多重背包和分组背包，还给出了它们的状态转移方程和代码实现。现在，咱们来聊聊这些背包问题到底在讲啥，以及它们能解决哪些问题。

引言
背包问题听起来很基础，但其实是一个经典的动态规划问题。在现实生活中，我们可以把这个模型想象成一个“怎么装下更多更有价值的东西”的问题。比如，你去旅行，只能带一个容量有限的背包，但有很多物品可以选，每个物品占据一定的空间，同时有不同的价值。这时候，你该如何装呢？这就是背包问题的核心。

相关问题
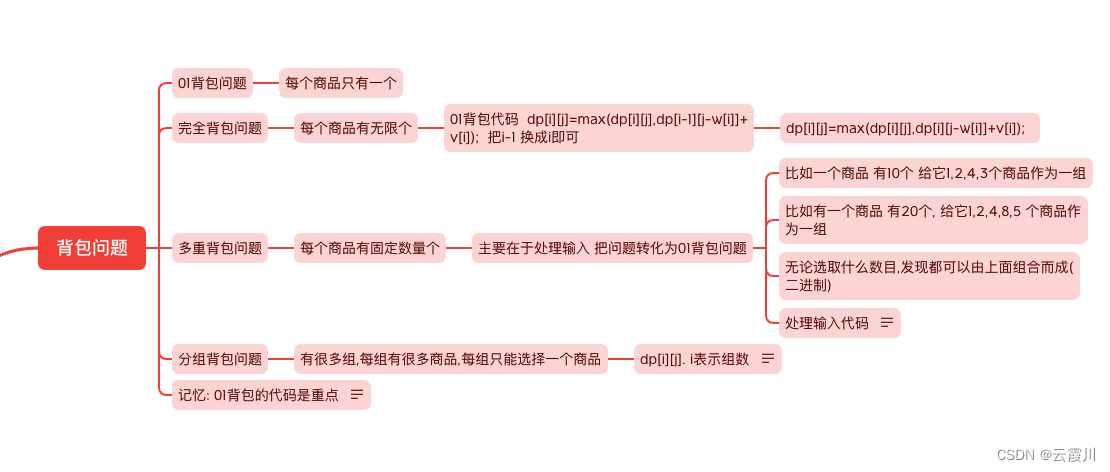
1. 01背包问题的核心是什么？
- 每个物品只能选一次。
- 方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
- 类比：就像在一个考试中选题，每个题目只能做一遍。

2. 完全背包问题怎么处理？
- 每个物品可以选无限次。这种情况下，状态方程变成了：
dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]] + v[i])
- 类比：你可以无限次购买某种商品，比如优惠券可以无限次使用。

3. 多重背包问题有什么特点？
- 每个物品有固定的数量限制。这种情况的实现可以用“二进制拆分”来优化。
- 类比：比如你有5个苹果，想知道怎么组合价值最高。

4. 分组背包问题怎么解决？
- 物品分组，每组只能选一个。状态方程类似多重背包。
- 类比：比如你有好几组衣服，只能选其中一组。

相关答案
1. 为什么动态规划能解决这样的问题？
- 因为动态规划通过记录子问题的解，避免了重复计算，从而提高了效率。
- 举个例子，假设你已经计算了装满容量5的背包的最大价值，那当你装容量6的时候，可以直接用已经算好的数据，而不需要从头计算。

2. 如何理解“二进制拆分”？
- 一个物品有k个，可以把k拆分成二进制的表示，把问题转化为01背包。
- 例如，k=5可以拆分成分成1、2、2（或者1、2、剩下的部分）。
- 这样做的好处是可以用01背包的方法来解，从而提高效率。

3. 分组背包有什么实际应用场景？
- 比如在工作中，你可以选择不同的项目组，每个项目组只能选一个项目，这时候分组背包就能帮助你最大化收益。

总结
背包问题不仅仅是装东西的问题，它更像是一种资源分配的优化问题。动态规划的思路在这里显得尤为重要，它让我们能够通过小问题的解决，逐步构建出整体的最优解。无论是装物品还是做选择，背包问题都给了我们一个思考和解决问题的方式。

如果你觉得这篇文章对你有帮助，不妨再深入研究一下动态规划的其他问题，比如最长递增子序列、矩阵链乘法等。这些看似复杂的问题，其实都有类似的解决思路。加油！

背包问题

容量有限的背包，给很多商品，商品有相应的体积与价值

01背包问题

一个背包 每个物品只有一个

最终状态方程

dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])

推导过程

由上一层推导过来

选择拿不拿i

最终代码

#include<iostream>
#include<vector>
using namespace std;
// 1 2 3 4 5 分别代表商品编号
int bag_01(int n,int b,vector<int> &v,vector<int> &w)
{// b 代表bag v代表价值 w代表weightvector<vector<int>> dp(n+1,vector<int>(b+1));//int dp[v.size()+1][b+1]; // 代表选完i产品，背包有b容积 能获得的最大价值// 当i=0时for(int i=1;i<=n;i++){for(int j=0;j<=b;j++){// 等于在背包容积允许的情况下给背包加了重量，同时也加入了价值dp[i][j]=dp[i-1][j];if(j>=w[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);}}return dp[n][b];
}int main()
{// dp[i][j] i 表示第i次选择 j表示剩余的体积int n=0;cin>>n;vector<int> v(n+1);vector<int> w(n+1);int b=0;cin>>b;for(int i=1;i<=n;i++){cin>>w[i]>>v[i];}cout<<bag_01(n,b,v,w)<<endl;
}

完全背包问题

每个商品无限个

最终状态方程

dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i])

推导过程

每个物品无限个,尝试为每个产品都尝试塞进去

for(int i=1;i<=n;i++)
{for(int j=0;j<=b;j++){for(int k=0;j*w[i]<=j;k++){dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);}}
}

可以转化为2维，[i][j]中与[i][j-w[i]] 有很相似的部分

[i][j]=max([i-1][j],[i-1][j-w]+v,[i-1][j-2w]+2v,[i-1][j-3w]+3v....)
[i][j-w]=max([i-1][j-w],[i-1][j-2w]+v,[i-1][j-3w]+2v....). 
[i][j]=max([i-1][j],[i][j-w]+v)

最终代码

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int whole_bag(int n,int b,vector<int> &v,vector<int> &w)
{//cout<<"进入"<<endl;vector<vector<int> > dp(n+1,vector<int>(b+1));for(int i=1;i<=n;i++){for(int j=0;j<=b;j++){dp[i][j]=dp[i-1][j];if(j>=w[i]){dp[i][j]=max(dp[i][j],dp[i][j-w[i]]+v[i]);}}}return dp[n][b];
}
int main()
{int n=0;cin>>n;vector<int> v(n+1);vector<int> w(n+1);int b=0;cin>>b;for(int i=1;i<=n;i++){cin>>w[i]>>v[i];}cout<<whole_bag(n,b,v,w)<<endl;
}

多重背包问题

每个物品数量不一样

推导过程

朴素解法，给k的数目加上一个限制

for(int i=1;i<=n;i++){for(int j=0;j<=b;j++){for(int k=0;k*w[i]<=j&&k<=s[i];k++){dp[i][j]=max(dp[i][j],dp[i-1][j-k*w[i]]+k*v[i]);}}}

看能否采用完全背包的优化方法呢？

[i][j]=max([i-1][j],[i-1][j-w]+v,[i-1][j-2w]+2v,[i-1][j-3w]+3v+...+[i-1][j-sw]+sw)
[i][j-w]=max([i-1][j-w],[i-1][j-2w]+v,[i-1][j-3w]+2v....+[i-1][j-sw]+(s-1)w+[i-1][j-(s+1)w]+sw). 
会发现[i][j-w] 多了一项，这就无法用max

采用二进制方法优化，将 多重背包问题 转化成 01背包问题

如一个商品有100个

1 个 作为一个商品

2 个 作为一个商品

4 个 作为一个商品

8 个 作为一个商品

.. 最后一个商品用剩余的数目当成整体商品

512 个 作为一个商品

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int bag_01(int n,int b,vector<int>&w,vector<int>&v)
{vector<vector<int> > dp(n+1,vector<int>(b+1));for(int i=1;i<=n;i++){for(int j=0;j<=b;j++){dp[i][j]=dp[i-1][j];if(j>=w[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i]]+v[i]);}}return dp[n][b];
}int main()
{int n_fake=0;cin>>n_fake;int b=0;cin>>b;int n=0;vector<int> v;vector<int> w;v.push_back(-1);w.push_back(-1);for(int i=1;i<=n_fake;i++){int l1,l2,l3;// l1 是 体积// l2 是 价值// l3 是 个数cin>>l1>>l2>>l3;int k=1;while(k>=l3){l3-=k;v.push_back(l2*k);w.push_back(l1*k);n+=1;k*=2;}if(l3!=0){v.push_back(l2*k);w.push_back(l1*k);}}cout<<bag_01(n,b,w,v)<<endl;}

分组背包问题

物品有n组，每组物品有若干个，每组最多选一个

分组背包问题

dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i,k]]+v[i,k])

选择第k个商品

类似多重背包问题的朴素写法,非常符合逻辑

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int group_bag(int n,int b,vector<vector<int> >& w,vector<vector<int> >& v)
{vector<vector<int> > dp(n+1, vector<int>(b+1));for(int i=1;i<=n;i++){for(int j=0;j<=b;j++){dp[i][j]=dp[i][j-1];for(int l=0;l<v[i].size();l++){if(w[i][l]<=j) dp[i][j]=max(dp[i][j],dp[i-1][j-w[i][l]]+v[i][l]);}}}return dp[n][b];
}
int main()
{vector<vector<int> > w;vector<vector<int> > v;int n=0;int b=0;cin>>n>>b;w.push_back(vector<int>(1));v.push_back(vector<int>(1));for(int i=1;i<=n;i++){int n1=0;cin>>n1;vector<int> v1(n1);vector<int> w1(n1);for(int j=0;j<n1;j++){int a=0;int b=0;cin>>a>>b;w1.push_back(a);v1.push_back(b);}w.push_back(w1);v.push_back(v1);}cout<<group_bag(n,b,w,v)<<endl;
}

欢迎大家 star ✨ GitHub - stolendance/acwing

正在更新算法模板   写上去就能用