数据结构刷新知识总结,为了与题目分开,特地在这里开一篇博客

文章目录
- 二叉树、树、森林的转换
- 二叉树的五个特性
- 常用算法总结
- 常用算法详解
- 图的概念
- 堆
- 排序
- 哈希
- 查找
二叉树、树、森林的转换
- 树转二叉树
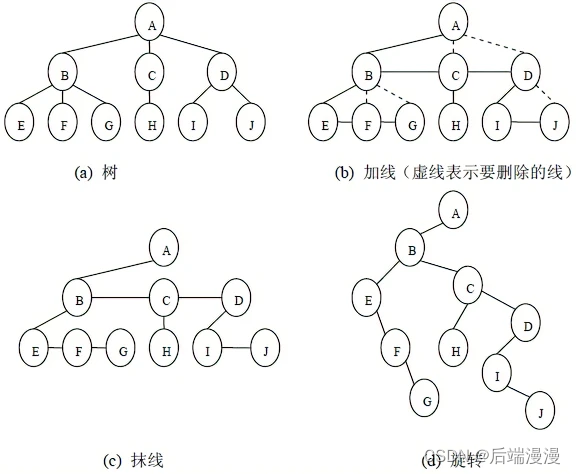
- 二叉树转树
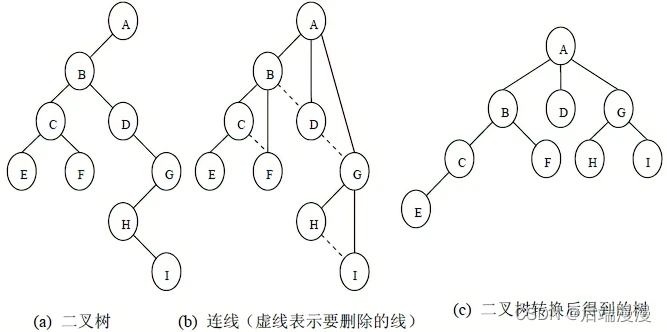
- 森林转二叉树
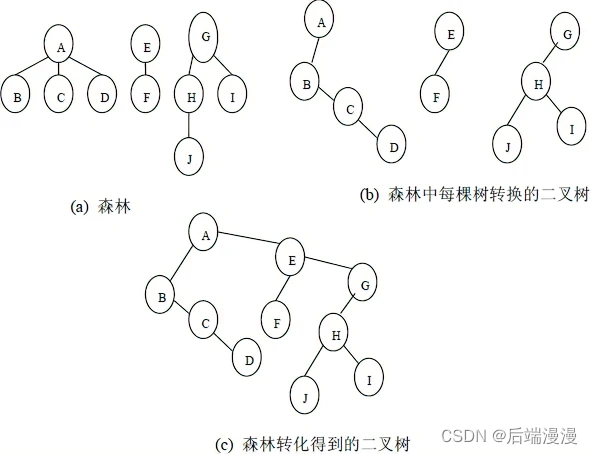
- 二叉树转森林
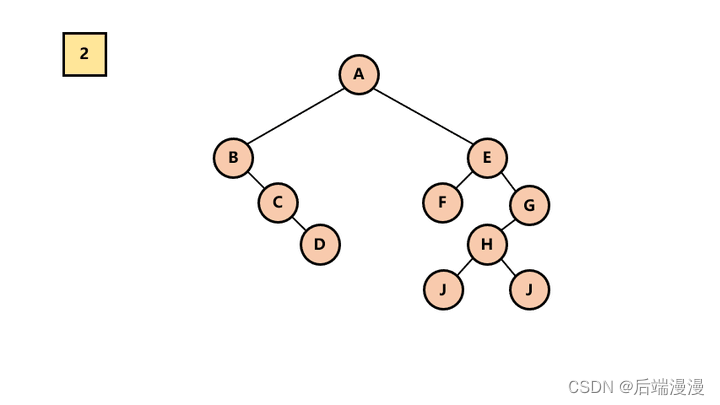
二叉树的五个特性
- 性质1:在二叉树的第i层上至多有2i-1个结点
- 性质2:深度为k的二叉树至多有2k-1个结点
- 性质3:具有n个节点的完全二叉树深为log2(n+1)
- 性质4:度为 0 的叶子结点总是比度为 2 的结点多一个n0 = n2 + 1
- 性质5:完全二叉树中,结点i的左孩子是2i,右孩子是2i+1
常用算法总结
- 最小生成树:Prim算法、Kruskal算法
- 最短路径:Dijkstra算法、Floyd算法、DFS算法、BFS算法、Ford算法
- 拓扑排序:AOV网
- 关键路径:AOE网
常用算法详解
- 广度优先遍历BFS

- 深度优先遍历

- Prim算法
- Kruskal算法
- Dijkstra算法:实现单源最短路径问题
- 算法介绍:Dijkstra算法应用了贪心算法思想,是目前公认的最好的求解最短路径的方法。
- 辅助数组
dist[]:记录从源点v0到其他各顶点当前的最短路径长度。
path[]:path[i]表示源点到顶点i之间的最短路径的前驱结点。- 算法思想:
设置一个集合S记录已求得的最短路径的顶点,初始时把源点v~0~放入S; 集合S每并入一个新顶点v ~i~ ,都要修改源点v ~0 ~到集合V-S中顶点当前的最短路径长度值;- 具体实例

- 拓扑排序
算法思想
- 从AOV网中选择一个没有前驱的顶点并输出
- 从网中删除该顶点和所有以它为起点的有向边
- 重复步骤1和步骤2直到当前AOV网为空
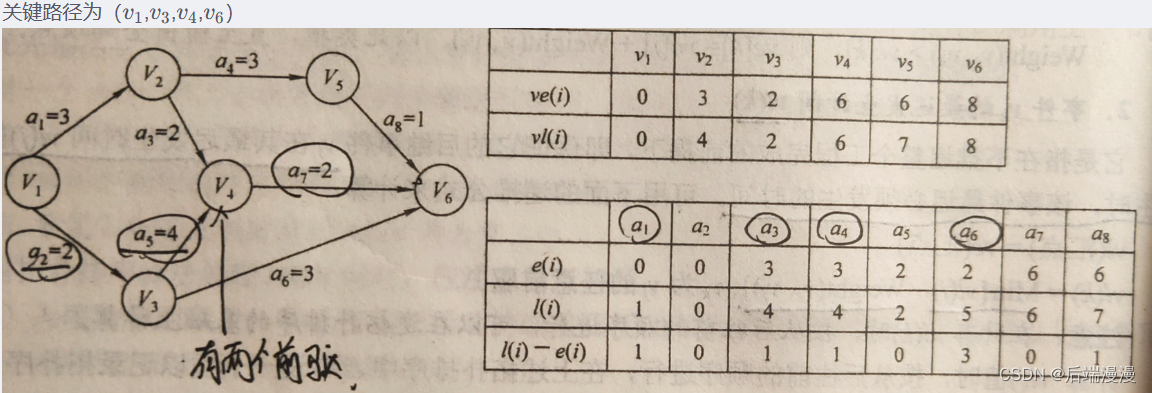
- 关键路径
算法思想
- 从源点出发,令ve(源点)=0,按拓扑排序求其余顶点的最早发生时间ve();
- 从汇点出发,令vl(汇点)=ve(汇点),按逆拓扑排序求其余顶点的最迟发生时间vl();
- 根据各顶点的ve()值求所有弧的最早开始时间e();
- 根据个顶点的vl()值求所有弧的最迟开始时间l();
- 求AOE网中所有差额d(),找出所有d()=0的活动构成关键路径
具体实例
图的概念
- 完全图:对于无向图来说有n(n-1)/2条边,对于有向图来说有n(n-1)条边
- 连通图:对于无向图来说,符合完全图的无向图就是连通图
- 强连通图:对于有向图来说,符合完全图的有向图就是强连通图
存储结构
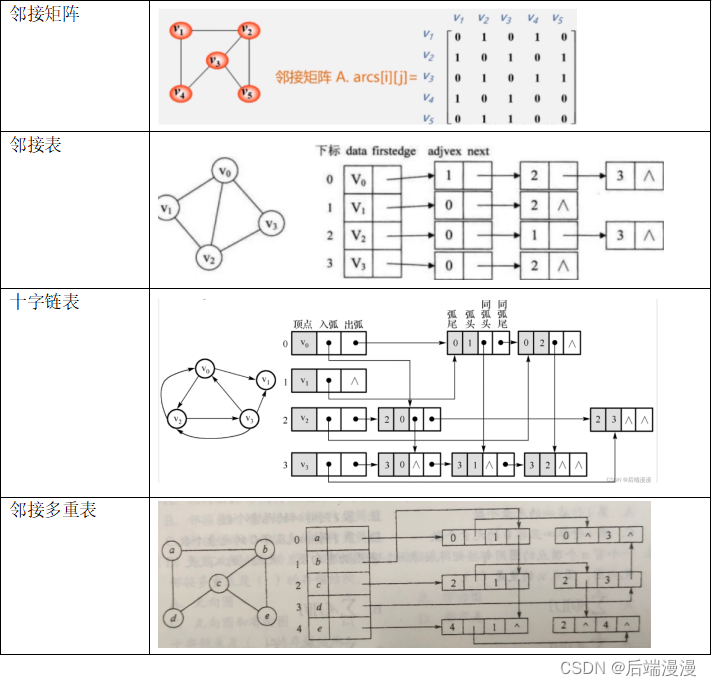
堆
注意:下标从1开始
- 堆:可以理解为顺序存储的完全二叉树
- 大根堆:完全二叉树,根>=左右
- 小根堆:完全二叉树,根<=左右
- 堆排序分为两个过程:堆初始化、输出堆顶后调整新堆
- 自下而上算法

排序
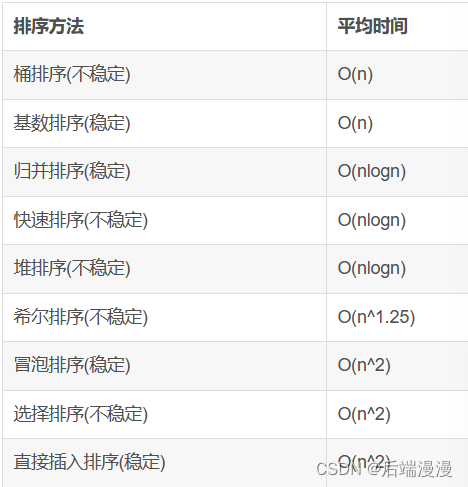
- 直接插入排序

- 折半插入排序
对直接插入排序算法的改进,在对有序部分进行折半查找并插入
-
希尔排序

-
冒泡排序

-
快速排序

-
简单选择排序

-
堆排序

-
归并排序
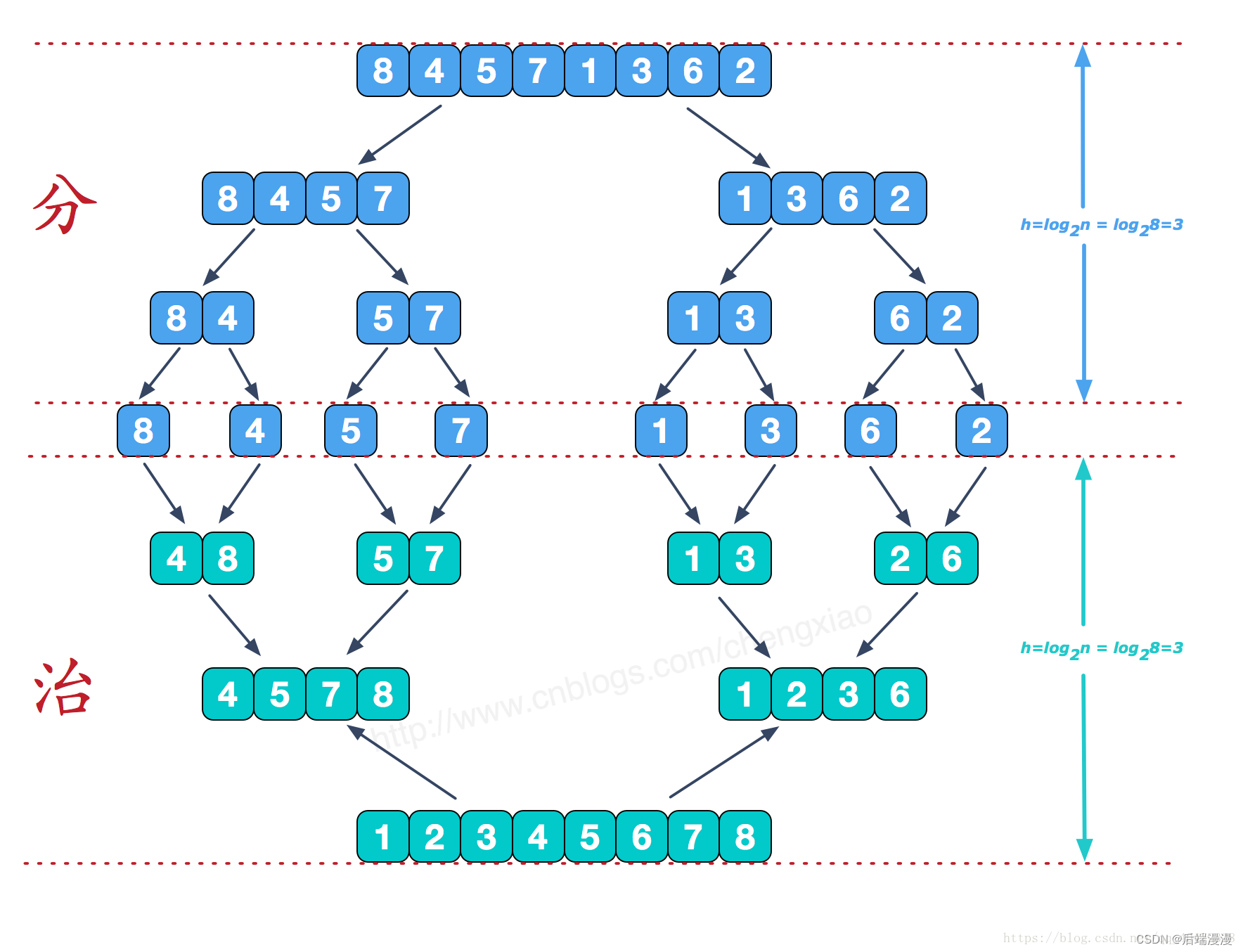
-
基数排序

哈希
- 散列函数
- 直接定址法:H(key)=a*key+b
- 除留余数法:H(key)=key%p
- 数字分析法:抽取关键字中分布较为均匀的若干位作为散列地址
- 平方取中法:关键字的平法值中间几位作为散列地址
- 处理冲突
- 线性探测法:Hi=(Hash(key)+did_idi)mod m,其中di=0,1,2,3…
- 平方探测法:Hi=(Hash(key)+did_idi)mod m,其中di=0,121^212,-121^212,222^222,-222^222…
- 伪随机序列法:Hi=(Hash(key)+did_idi)mod m,其中di=伪随机序列法
- 双散列法 : Hi=(Hash(key)+i*did_idi)mod m,其中di=Hash2Hash_2Hash2(key)
- 链接法:把所有的同义词存储在一个线性链表中,这个线性链表可以由其散列地址唯一标识。
- 散列查找
- 检测表中地址为Addr的位置上是否有记录,若无记录,返回查找失败;
若有记录,比较Addr对应元素与关键字,如相等则返回查找成功的标记;
否则执行步骤2- 用给定的冲突处理方法计算下一个散列地址,并把Addr置为此地址,转入步骤1
查找
1. 线性结构
- 顺序查找
- 折半查找
- 分块查找:块内无序,块之间有序。即第一个块中的最大关键字小于第二个块中的所有记录的关键字
2. 树形结构
- 二叉排序树BST
- 二叉平衡树
- 红黑树
- B树
- B+树
3. 散列结构