LeetCode算法小抄--花式遍历二叉树

⚠申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计3545字，阅读大概需要3分钟
🌈更多学习内容， 欢迎👏关注👀【文末】我的个人微信公众号：不懂开发的程序猿
个人网站：https://jerry-jy.co/

花式遍历二叉树

翻转二叉树

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

// 用「遍历」的思维模式
class Solution {public TreeNode invertTree(TreeNode root) {// 遍历二叉树，交换每个节点的子节点traverse(root);return root;}private void traverse(TreeNode root){if(root == null) return;/ 前序位置 /// 每一个节点需要做的事就是交换它的左右子节点 TreeNode temp = root.left;root.left = root.right;root.right = temp;// 遍历框架，去遍历左右子树的节点traverse(root.left);traverse(root.right);}
}

可以用 invertTree(x.left) 先把 x 的左子树翻转，再用 invertTree(x.right) 把 x 的右子树翻转，最后把 x 的左右子树交换，这恰好完成了以 x 为根的整棵二叉树的翻转，即完成了 invertTree(x) 的定义。

// 用「分解问题」的思维模式
class Solution {// 定义：将以 root 为根的这棵二叉树翻转，返回翻转后的二叉树的根节点public TreeNode invertTree(TreeNode root) {if(root == null) return null;// 利用函数定义，先翻转左右子树TreeNode left = invertTree(root.left);TreeNode right = invertTree(root.right);// 然后交换左右子节点root.left = right;root.right = left;// 和定义逻辑自恰：以 root 为根的这棵二叉树已经被翻转，返回 rootreturn root;}
}

这种「分解问题」的思路，核心在于你要给递归函数一个合适的定义，然后用函数的定义来解释你的代码；如果你的逻辑成功自恰，那么说明你这个算法是正确的。

填充节点的右侧指针

116. 填充每个节点的下一个右侧节点指针

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {int val;Node *left;Node *right;Node *next;
}

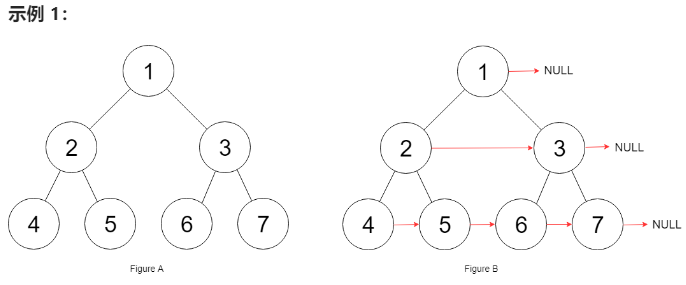
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

很容易写出以下代码：

// 错误的，因为它只能把相同父节点的两个节点穿起来
class Solution {public Node connect(Node root) {traverse(root);return root;}private void traverse(Node root){if(root == null || root.left == null) return;// 把左子节点的 next 指针指向右子节点root.left.next = root.right;traverse(root.left);traverse(root.right);}
}

节点 5 和节点 6 不属于同一个父节点，那么按照这段代码的逻辑，它俩就没办法被穿起来

传统的 traverse 函数是遍历二叉树的所有节点，但现在我们想遍历的其实是两个相邻节点之间的「空隙」。

所以我们可以在二叉树的基础上进行抽象，你把图中的每一个方框看做一个节点：

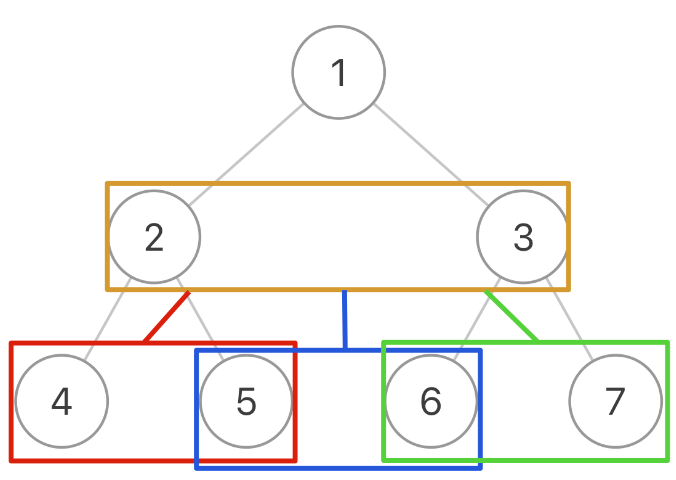
一棵二叉树被抽象成了一棵三叉树，三叉树上的每个节点就是原先二叉树的两个相邻节点

现在，我们只要实现一个 traverse 函数来遍历这棵三叉树，每个「三叉树节点」需要做的事就是把自己内部的两个二叉树节点穿起来

/*
// Definition for a Node.
class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
*/class Solution {public Node connect(Node root) {if(root == null) return null;traverse(root.left, root.right);return root;}// 三叉树遍历框架private void traverse(Node node1, Node node2){if(node1 == null || node2 == null) return;/ 前序位置 /// 将传入的两个节点穿起来node1.next = node2;// 连接相同父节点的两个子节点traverse(node1.left, node1.right);traverse(node2.left, node2.right);// 连接跨越父节点的两个子节点traverse(node1.right, node2.left);}
}

将二叉树展开为链表

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

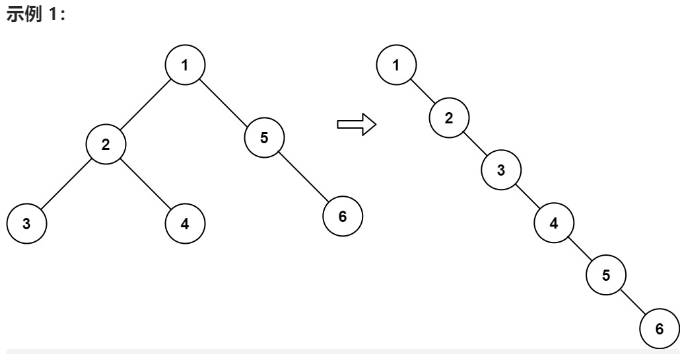
思路

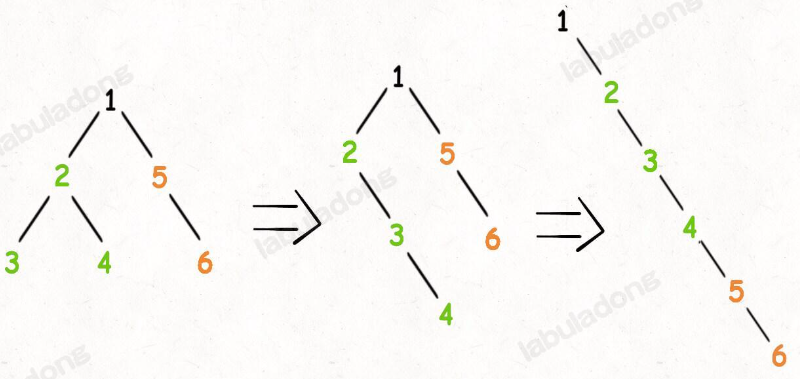
对于一个节点 x，可以执行以下流程：

1、先利用 flatten(x.left) 和 flatten(x.right) 将 x 的左右子树拉平。

2、将 x 的右子树接到左子树下方，然后将整个左子树作为右子树。

/* Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {// 定义：将以 root 为根的树拉平为链表public void flatten(TreeNode root) {// base caseif(root == null) return;// 利用定义，把左右子树拉平flatten(root.left);flatten(root.right);/ 后序遍历位置 /// 1、左右子树已经被拉平成一条链表TreeNode left = root.left;TreeNode right = root.right;// 2、将左子树作为右子树root.left = null;root.right = left;// 3、将原先的右子树接到当前右子树的末端TreeNode p = root;while(p.right != null){p = p.right;}p.right = right;}}

总结

二叉树解题的思维模式分两类：

1、是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现，这叫「遍历」的思维模式。

2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

–end–