功率因素角和电压电流的相位差相等

功率因素角和相位差相等,电路分析中给了结论,但没有给出证明过程。其次,对余弦函数的积分了解不够深刻。最后在电气工程师考试题目也会经常遇到。
功率因数表示一个负荷所需要的有功功率和视在功率的比值。
即cosφ=P/S,
其中:
P为有功功率
Q为无功功率
S为视在功率:S = U*I
cosφ为功率因数,φ为功率因数角。
相位差:电压与电流之间的时间差为ψ,cosφ= cosψ,为什么?
余弦积分计算:
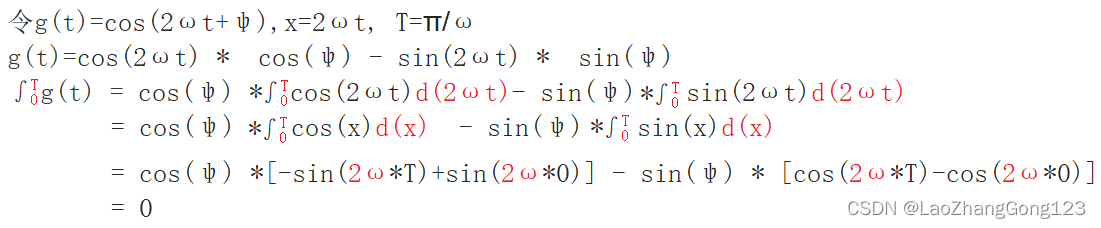
有功功率计算:
已知u=Um * sin(ωt),i=Im * sint(ωt+ψ),有效值为U和I,
则:
相位差:电压与电流之间的时间差为ψ
p(t) = Um * cos(ωt) * Im * cos(ωt+ψ)
= Um * Im * cos(ωt) * cos(ωt+ψ)
= Um * Im * [ cos(2ωt+ψ) + cos(ψ) ] / 2
= U * I * [ cos(2ωt+ψ) + cos(ψ) ]

又因为P=S * cosφ,
所以cosφ=cos(ψ)
相位差是指电压与电流之间的时间差,通常用θ表示
cosθ= cosφ
高等数学,没有学好,可能存在理解和计算错误,欢迎交流。
