( “树” 之 DFS) 617. 合并二叉树 ——【Leetcode每日一题】

在这个问题中，我们探讨的是合并二叉树的问题，这是一个涉及树结构的经典算法问题。通过观察我们可以发现，合并二叉树的关键在于理解如何将两个树合并为一个新树，同时保持节点值的正确性和树的结构。

理解问题的核心:

合并二叉树的基本思想是将两个树的节点值相加，得到新树的节点值。如果两个树的节点值不同，那么新树的这个节点就设为两者之和。此外，如果两个树的同一层节点都有子树，那么子树的节点将通过递归的方式合并，这保证了树的整体结构得以保留。

如何解决问题:

1. 递归处理每个节点: 每个节点的合并策略是根据左右子树的合并结果来确定的。如果一个节点在原树中不存在，那么另一个树中的对应节点将成为此新节点的子节点。

root1->val += root2->val;
root1->left += mergeTrees(root1->left, root2->left);
root1->right += mergeTrees(root1->right, root2->right);

2. 处理边界情况: 如果其中一个树为空，另一个树的相应节点将直接成为新树的节点，这避免了在空树中寻找节点的错误。

代码示例和解释:

在Java和C++中，我们提供了代码示例。这些代码展示了如何使用递归和合并策略来解决这一问题。通过阅读代码，我们可以更好地理解如何在实际中应用这些策略。

深入思考与应用:

这个问题不仅是一个简单的数据结构问题，它还涉及到递归和树结构的深刻理解。通过解决这类问题，我们可以加深对树的结构和动态变化的理解，同时提升我们处理复杂数据结构问题的能力。此外，这个问题也经常出现在实际的编程问题中，特别是在需要处理树形数据结构的项目中。

总之，617. 合并二叉树问题是一个很好的例子，展示了如何将理论知识应用到具体的编程问题中，同时也提供了一个加深对树结构理解的机会。通过解决这类问题，我们可以在编程和算法领域获得更深入的洞察力和更高级的技能。

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

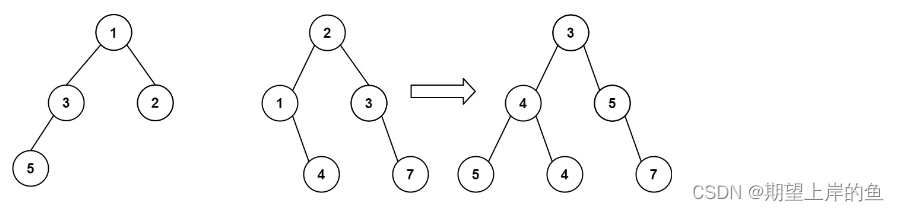
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

提示：

• 两棵树中的节点数目在范围 [0, 2000] 内
• −104<=Node.val<=104-10^4 <= Node.val <= 10^4−104<=Node.val<=104

思路：递归 DFS

1、首先要清楚我们要写的递归函数返回什么？

• 这里的mergeTrees返回合并后的头结点；

2、然后考虑边界，就是什么时候返回return，以及是否需要合并：

• 如果root1和root2中有一个节点为空，则不需要合并，直接另外一个节点即可；
• 如果都不空，则需要合并，可以将root2合并到root1，不用再申请新的节点；
• 当前节点处理完，在递归处理左子树和右子树；
• 返回合并后的头结点root1.

代码：(Java、C++)

Java

/* Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1 == null) return root2;if(root2 == null) return root1;root1.val += root2.val;root1.left = mergeTrees(root1.left, root2.left);root1.right = mergeTrees(root1.right, root2.right);return root1;}
}

C++

/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1 == NULL) return root2;if(root2 == NULL) return root1;root1->val += root2->val;root1->left = mergeTrees(root1->left, root2->left);root1->right = mergeTrees(root1->right, root2->right);return root1;}
};

运行结果：