一、线段数Segment Tree

也叫 区间树

1.1 线段树的优势

一面墙，长度n，每次选择一段染色

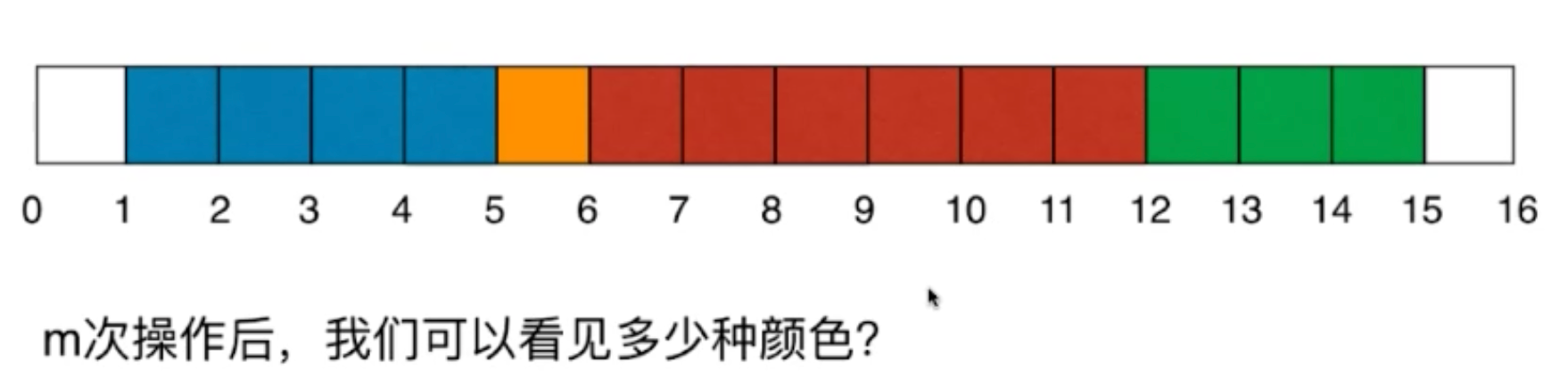
关注的是一个个区间

染色操作：更新区间
查询

1.1.2 数组实现线段树

可以很快想到直接用 数组 实现

数组实现时间复杂度很高，需要优化

1.2 线段树结构

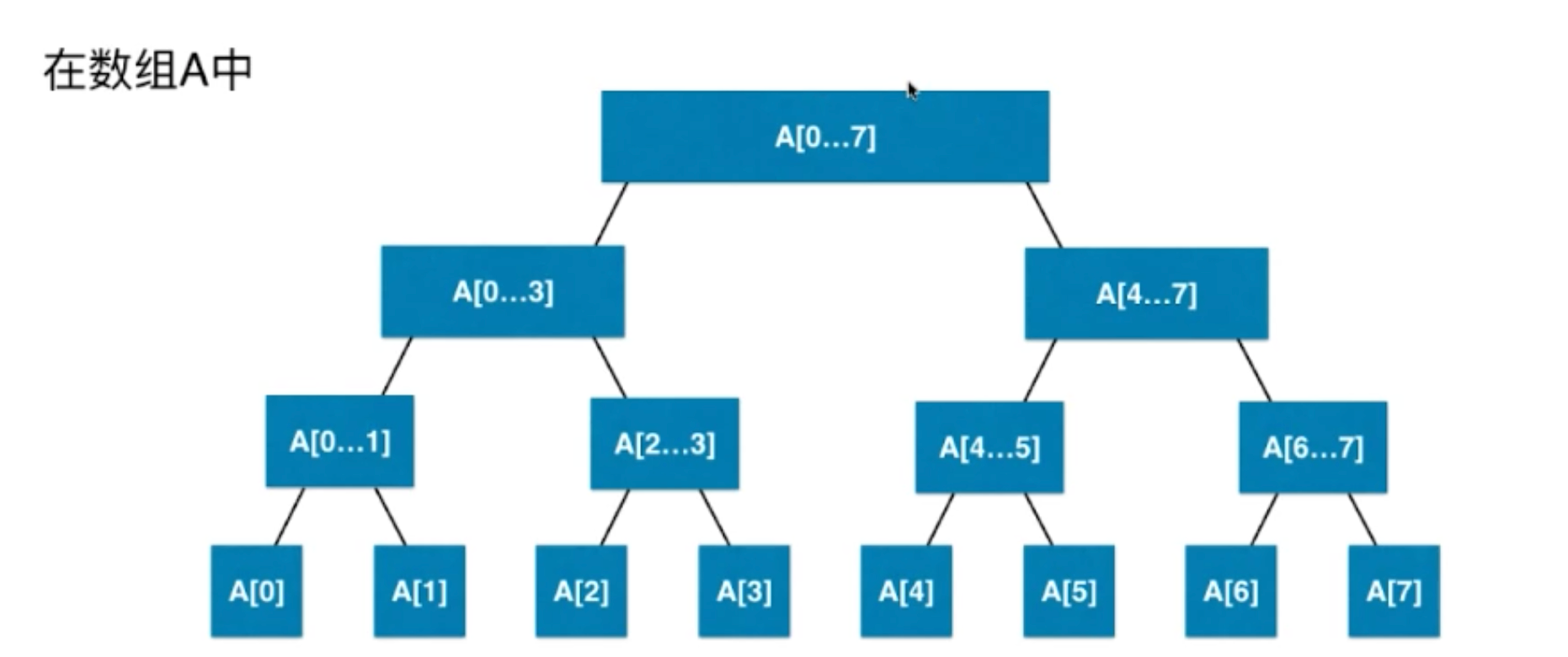
数组嵌套链表

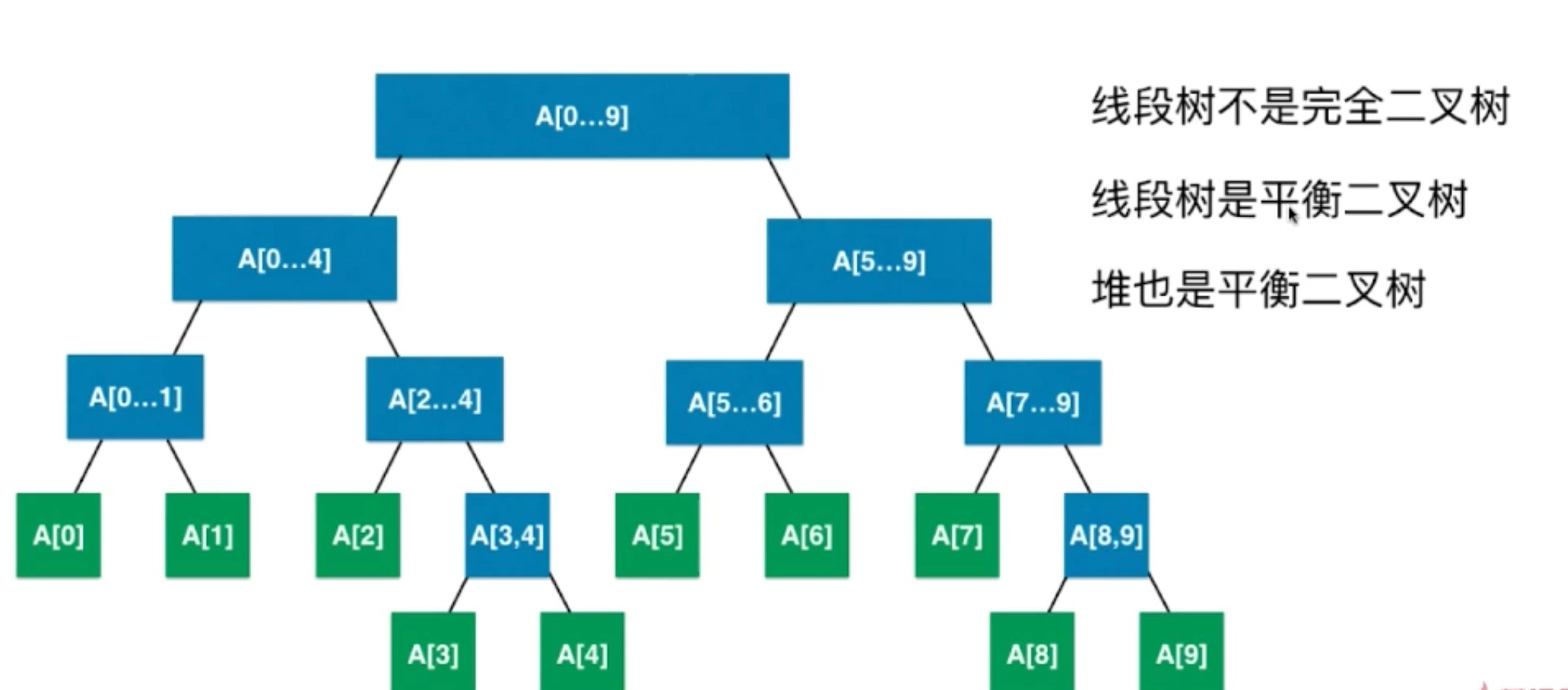
平衡二叉树：最大层 - 最小层 <= 1

1.2.1 数组的节点

区间有n个元素，数组要有多少？

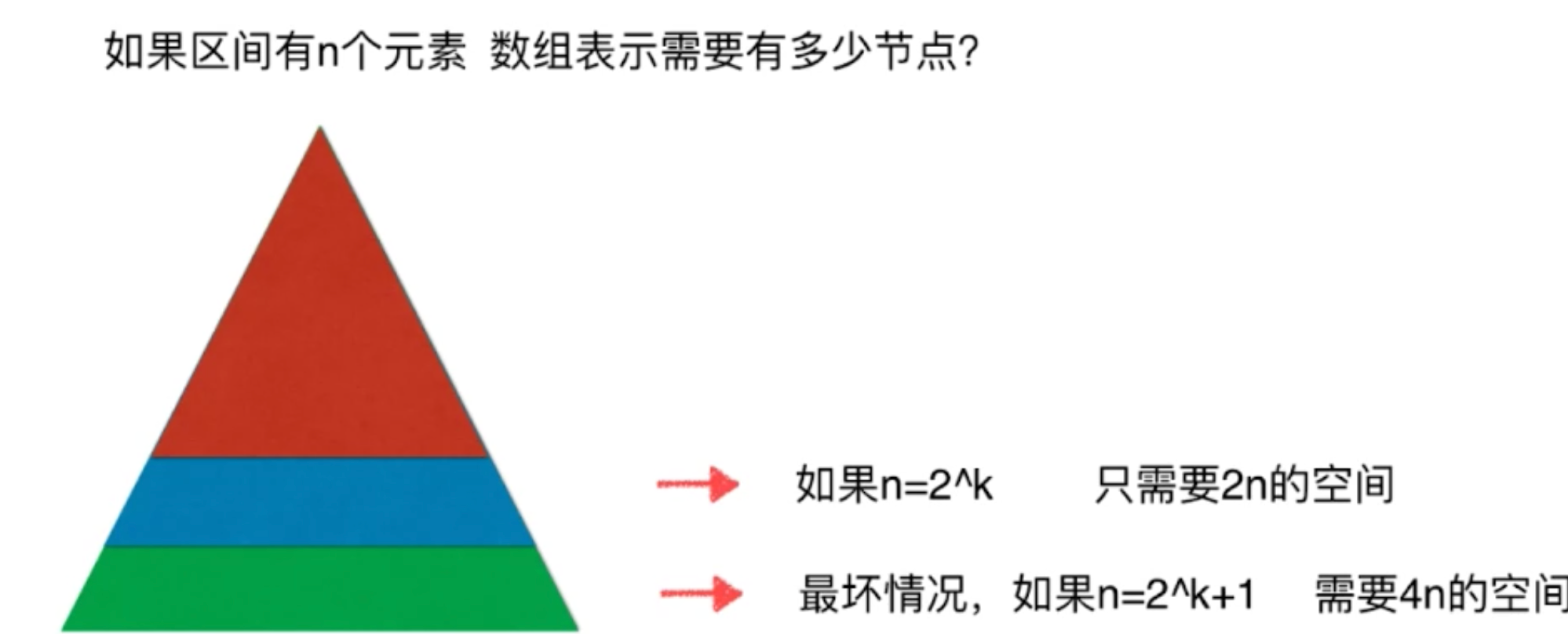
最差的情况4n，有接近一半的空间是浪费：

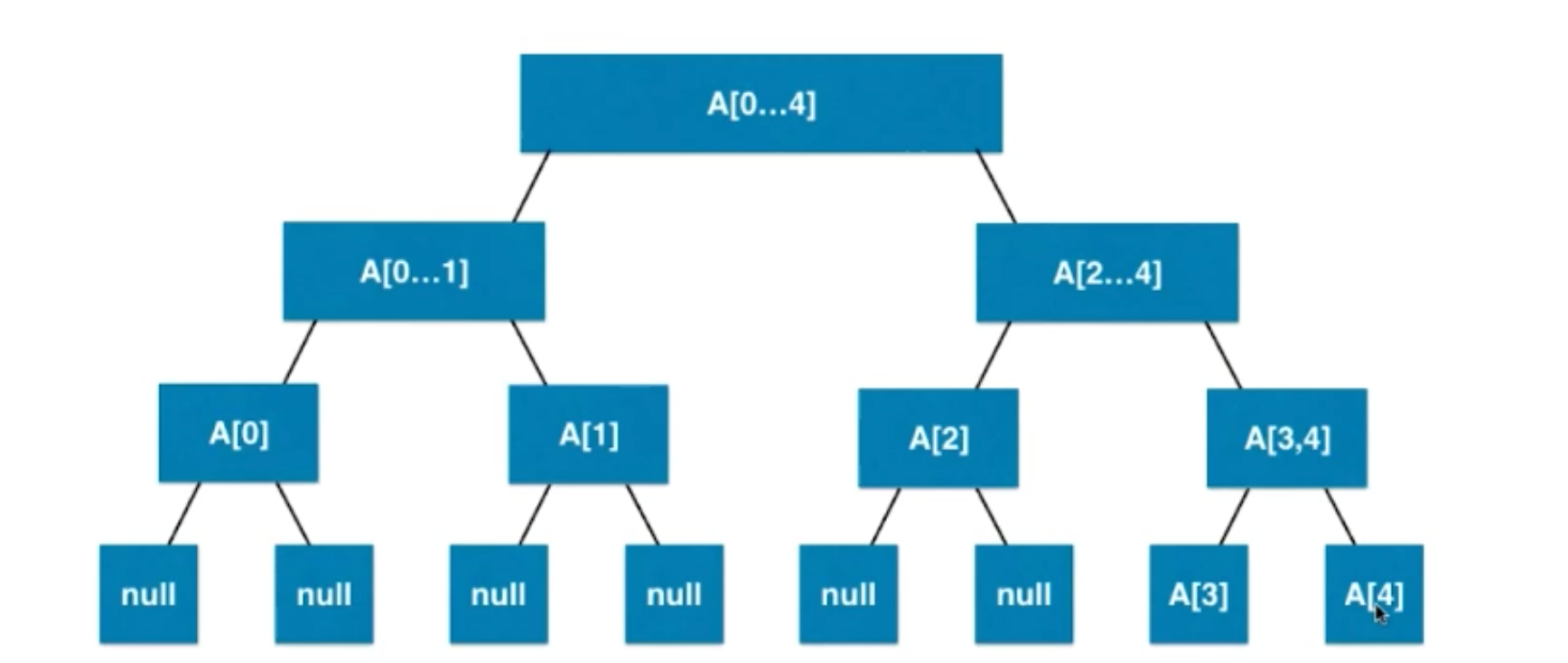
public class SegmentTree<E> {private E[] tree;private E[] data;private Merger<E> merger;public SegmentTree(E[] arr, Merger<E> merger){this.merger = merger;data = (E[])new Object[arr.length];for(int i = 0 ; i < arr.length ; i ++)data[i] = arr[i];tree = (E[])new Object[4 * arr.length];buildSegmentTree(0, 0, arr.length - 1);}// 在treeIndex的位置创建表示区间[l...r]的线段树private void buildSegmentTree(int treeIndex, int l, int r){if(l == r){tree[treeIndex] = data[l];return;}int leftTreeIndex = leftChild(treeIndex);int rightTreeIndex = rightChild(treeIndex);// int mid = (l + r) / 2;int mid = l + (r - l) / 2;buildSegmentTree(leftTreeIndex, l, mid);buildSegmentTree(rightTreeIndex, mid + 1, r);tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);}public int getSize(){return data.length;}public E get(int index){if(index < 0 || index >= data.length)throw new IllegalArgumentException("Index is illegal.");return data[index];}// 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引private int leftChild(int index){return 2*index + 1;}// 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引private int rightChild(int index){return 2*index + 2;}@Overridepublic String toString(){StringBuilder res = new StringBuilder();res.append('[');for(int i = 0 ; i < tree.length ; i ++){if(tree[i] != null)res.append(tree[i]);elseres.append("null");if(i != tree.length - 1)res.append(", ");}res.append(']');return res.toString();}
}