一. 浮点数存储时是有精度损失的

下面程序中我们打印一个浮点数的值

int main()
{double d = 3.6;printf("%.50f\\n", d);return 0;
}

观察到浮点数存储在内存空间中是有内存损失的：

二. 浮点数不能直接进行 == 比较

所有存储在内存中的浮点数都不能做到完全精确，如果拿它们进行计算，那误差更是在所难免。

int main()
{double x = 1.0;double y = 0.1;printf("%.50f\\n", x - 0.9);// 预计得到0.1printf("%.50f\\n", y);if ((x - 0.9) == y){printf("you can see me!\\n");}else{printf("oops!\\n");}return 0;
}

编译运行：

三. 使用精度来比较两个浮点数是否相等

既然浮点数的误差在所难免，那么我们可以考虑两个浮点数相等的条件是：它们差值的绝对值是一个很小的数的话，那么可以说这两个浮点数是相等的。

我们可以自定义一个最小差值，或者叫最小精确度EPSILON，它的值是 0.0000001

#define EPSILON 0.0000001int main()
{double x = 1.0;double y = 0.1;printf("%.50f\\n", x - 0.9);printf("%.50f\\n", y);// 另一种写法：// if(((x - 0.9) - y) > -EPSILON && ((x - 0.9) - y) < EPSILON)if (fabs((x - 0.9) - y) < EPSILON){printf("you can see me!\\n");}else{printf("oops!\\n");}return 0;
}

编译运行：

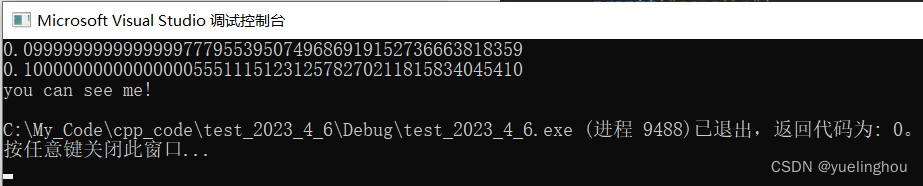
实际比较时，有各种各样的数据，这个最小精度我们不好掌握的话，可以使用系统提供的最小精度：

• #define DBL_EPSILON 2.2204460492503131e-016 // smallest such that 1.0+DBL_EPSILON != 1.0
• #define FLT_EPSILON 1.192092896e-07F // smallest such that 1.0+FLT_EPSILON != 1.0

四. 浮点数和0比较

上面我们知道了判断两个浮点数是否相等的方法就是看

if ( fabs(x - y) < DBL_EPSILON)

这个条件是否成立。

是否可以以此类推，判断一个浮点数 x 是否和 0 相等的话就是看

if ( fabs(x - 0) < DBL_EPSILON) 即 if ( fabs(x) < DBL_EPSILON)

下面用一段代码举例：

int main()
{double x = 0.000000000000000000000001;if (fabs(x) < DBL_EPSILON){printf("x == 0.0\\n");}else{printf("x != 0.0\\n");}return 0;
}

编译运行：

还有一个问题，就是用绝对值和 DBL_EPSILON 进行比较时能否用 <= 呢？

我们在来看看 DBL_EPSILON 是怎么定义的：

所有两个浮点数如果要相等，那它们差值的绝对值肯定是要小于DBL_EPSILON的，相等都不行。