AtCoder Regular Contest 159（A，B）

A

题目大意：
给你一个n$\ast$n的矩阵，矩阵中只有0和1，然后给的k是复制2k^ kk 个所给的n*n矩阵，每行放k个n$\ast$n矩阵,一共放k行。算最短路（0为没路，1为边权为1的路)
思路：
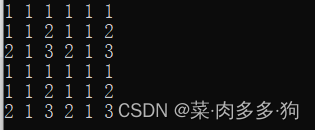
n很小，k很大，复制2k^kk个肯定做不到，猜测只需要原矩阵直接计算最短路，然后查询所输入的点%n。用第一个样例复制一下验证一下猜测：
这是通过Floyd算过的最短路之后的距离矩阵，可见复制的四个3 $\ast$ 3方块完全一样。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define INF 0x3f3f3f3fvoid solve()
{int n, k;cin >> n >> k;int a[n][n];memset(a, 0x3f, sizeof a);for(int i = 0; i < n; i ++ )for(int j = 0; j < n; j ++ ){int x;cin >> x;if(x) a[i][j] = x;}for(int k = 0; k < n; k ++ )for(int i = 0; i < n; i ++ )for(int j = 0; j < n; j ++ )a[i][j] = min(a[i][j], a[i][k] + a[k][j]);int q;cin >> q;while(q -- ){LL s, t;cin >> s >> t;s --, t --;int tmp = a[s % n][t % n];if(tmp == INF){cout << -1 << endl;}else{cout << tmp << endl;}}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;while(t -- ) solve(); system("pause");    return 0;
}

B

每进行一次题目所说的操作相当于a变成了g$\ast$(a/g - 1)，b变成了g$\ast$(b/g - 1)，且新的a和b的g会大于（之前g的倍数）等于旧的g。
如果a和b相等，减一次就够
如果a和b相差1，那么每次操作就只能减1，进行的操作数就是min(a,b)
直接将a和b除等于g，如果a和b不互质就一直除到互质。需要找到一个最小的t使得gcd（a-t，b-t）min，这个t就是将a和b变成a-t和b-t需要的操作数。设gcd（a-t，b-t）=k，a-t = k$\ast$ka, b-t = k$\ast$kb, 两式相减可得k能整除a和b的差值，那枚举k，求最小t

#include <bits/stdc++.h>
#pragma GCC optimize(3,"Ofast","inline")
using namespace std;
typedef long long LL;
#define int LLint solve(int a, int b)
{if(a == b) return 1;if(!a || !b) return 0;int d = abs(a - b);if(d == 1) return min(a, b);int g = __gcd(a, b);a /= g;b /= g;if(g > 1) return solve(a, b);if(a > b) swap(a, b); //不交换也一样int t = a % d;for(int i = 2; i <= d / i; i ++ ){if(d % i == 0){t = min(t, a % i);t = min(t, a % (d / i));}}a -= t;b -= t;return solve(a, b) + t;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int t = 1;// cin >> t;int a, b;cin >> a >> b;while(t -- ) cout << solve(a, b) << endl; system("pause");    return 0;
}