数学分析：多元微积分1

卓里奇的数学分析的好处在于直接从多元函数来入手多元微积分，引出矩阵，十分自然。

紧集的概念，感觉直接用闭集去理解就行，（对于图形学来说）。

多元函数的极限，其实和单元函数并没有什么区别。

 这里引出了完备度量空间的概念，其实我一开始也没明白为什么基本点列会没有极限，后来查了才知道，对于一个开区间(a,b),如果它的基本点列最终的极限是b，那么因为b不在这个空间中，所以我们认为这个空间不是完备度量的空间。

 这个还挺有意思的，对于极限趋于无穷的写法是，对于任何球的邻域，都可以找到一组基，使得这组基对应的像都不在这个球中。换句话说，再大的球，我们都可以找到一组基，使得基里的每个像都比这个球还要大，这就是无穷。

这里引出了道路的定义，就是一个区间I到R^n的连续映射。一般来说，就是闭区间[a,b]，

根据f(t)=R^n的映射建立的道路。

一致连续的意思是，对于任何，都可以找到一个足够小的区间，在这个区间上的任何两点对应的像的距离都小于它。

这里面强调的紧集，可以理解成闭集（对于图形学）。

 这是数学分析这本书里面的简写，但我感觉对于不习惯的人来说，理解起来很费劲。还是尽量用求和公式来表示吧。

 我们把(7)用普通的求和公式来写：

具体子母上我做了调整。不过这里也可以看到爱因斯坦符号的好处，确实非常简洁。

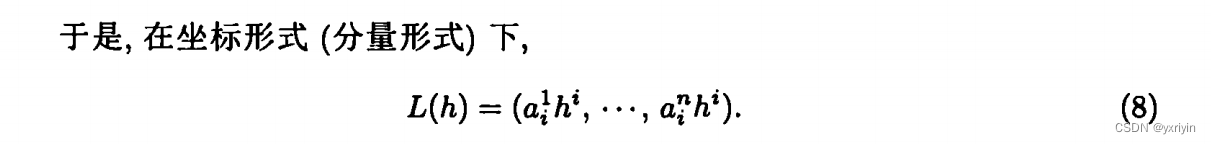
我们挑第一个分量验证下，

确实就是(8)

写成矩阵形式，就是（10），所以线性映射对应一个矩阵，而自变量对应一个向量，结果也是一个向量。

 这是范数的定义，就是我们常规理解下的距离。

接下来的内容是非常重要的，我觉得有必要单独另起一篇来讲