【深度学习】常见优化算法的PyTorch实现

优化算法（Optimization Algorithms）

深度学习的优化算法主要是解决神经网络的参数优化问题。在深度学习中，我们需要不断调整神经网络的参数，以使得神经网络的预测结果更加准确。而优化算法就是用来调整神经网络参数的算法。

优化算法的目标是找到一组参数，使得神经网络的预测结果与实际结果之间的误差最小。最常用的优化算法是梯度下降算法，其基本思想是在每一步迭代中，沿着损失函数的梯度方向更新参数，使得损失函数的值不断减小，从而使得神经网络的预测结果更加准确。

import torch
import torch.utils.data as Data
import torch.nn.functional as F  # 包含激励函数
import matplotlib.pyplot as plt

LR = 0.01  # 学习率
BATCH_SIZE = 32
EPOCH = 10

# 伪数据
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1 * torch.normal(torch.zeros(*x.size()))# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()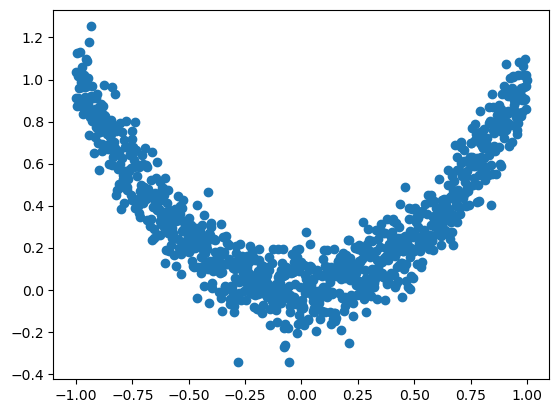

# DataLoader 是 torch 用来包装开发者自己的数据的工具.
# 将自己的 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中.
# 使用 DataLoader 的好处就是他们帮你有效地迭代数据# 先转换成 torch 能识别的 Dataset
# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
# 把 dataset 放入 DataLoader
loader = Data.DataLoader(dataset=torch_dataset,batch_size=BATCH_SIZE,shuffle=True,num_workers=2,
)  # 随机打乱数据 (打乱比较好)# 每个优化器优化一个神经网络# 默认的 network 形式
# default network
class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.hidden = torch.nn.Linear(1, 20)  # 隐藏层self.predict = torch.nn.Linear(20, 1)  # 输出层def forward(self, x):x = F.relu(self.hidden(x))  #添加激活函数x = self.predict(x)  # 输出return x

四种用于优化神经网络训练的算法，它们的全称及解释如下：

1.SGD（Stochastic Gradient Descent）随机梯度下降算法：指每次更新时只考虑随机抽取的一个样本数据，而不是全部数据，可以大大加快训练速度。但是它比较容易陷入局部最优解，并可能因数据抖动和噪声误差而导致不稳定的收敛速度和难以调整的学习率。

1.SGD (Stochastic Gradient Descent) algorithm: This algorithm considers only one randomly selected sample at a time during each update, instead of considering all the data, which can greatly accelerate the training speed. However, it is prone to getting stuck in local optimal solutions and may result in unstable convergence speed and difficult-to-adjust learning rates due to data jitter and noise errors."

2.Momentum（动量）：是在SGD基础上加上了惯性项，以避免SGD的两个问题，一方面增加了更新时考虑历史梯度信息的权重，另一方面减少了更新的方差，从而提高收敛速度和稳定性。其中动量参数决定了只考虑历史梯度的权重有多大，一般取值0.9左右。

2.Momentum: It adds an inertia term to SGD to avoid two problems with SGD. On the one hand, it increases the weight of considering historical gradient information during updates. On the other hand, it reduces the variance of updates, thereby improving convergence speed and stability. The momentum parameter determines how much weight to give to historical gradients and is generally set to about 0.9.

3.RMSProp（Root Mean Square Propagation）算法：主要是针对Adam的变量自适应调整学习率问题而提出的一种算法。它主要是对SGD算法引入了一个梯度平方加权平均项，从而使得学习率能够自适应地调整。具体地说，它在更新时除以了梯度的标准差来归一化梯度，从而可以对不同的梯度做出不同的调节。当然，它的超参数也会影响到效果。

3.RMSProp (Root Mean Square Propagation) algorithm: It is an algorithm mainly designed to address the issue of adaptive learning rate adjustment in Adam. It introduces a gradient square weighted average term to SGD, which enables the learning rate to adaptively adjust. Specifically, it normalizes the gradient by dividing it by the standard deviation during updates, which allows for different adjustments to be made for different gradients. Of course, its hyperparameters also affect its effectiveness.

4.Adam（Adaptive Moment Estimation）算法：Adam算法是SGD和动量算法的结合体，并引入了RMSProp算法的思想。它主要是将学习率自适应地调整为每个参数的自适应学习率，并且它可以防止随时间而逐渐降低的实际学习率逐渐逼近于零而导致收敛速度过慢的问题。同时，还能够对超参数进行调整，以适应不同的问题和数据集。Adam算法已经成为了许多机器学习工程师进行神经网络训练的首选算法之一。

4.Adam (Adaptive Moment Estimation) algorithm: Adam is a combination of SGD and momentum algorithms, incorporating the idea of RMSProp. It adapts the learning rate to each parameter's adaptive learning rate and prevents the actual learning rate from gradually approaching zero over time, thus avoiding the problem of slow convergence speed. Additionally, it can adjust hyperparameters to suit different problems and datasets. Adam has become one of the preferred algorithms for many machine learning engineers to train neural networks.

• SGD（随机梯度下降）

其中，表示第t次迭代后的权重，表示损失函数对于权重的梯度，表示学习率。

• Adam（自适应矩估计优化算法）

其中，和分别表示梯度的一阶矩估计和二阶矩估计，和分别表示偏差修正后的一阶矩估计和二阶矩估计，和分别表示一阶矩估计和二阶矩估计的衰减率，为防止分母为0的小数。

• RMSprop（均方根传播）

其中，表示梯度，表示梯度平方的指数加权平均数，为指数加权平均数的衰减率，为防止分母为0的小数。

• Adagrad（自适应梯度算法）

其中，表示梯度，表示梯度平方的累积和，为防止分母为0的小数。

• Adadelta（自适应学习率算法）

其中，表示梯度，表示梯度平方的指数加权平均数，表示参数更新值的指数加权平均数，为指数加权平均数的衰减率，为防止分母为0的小数。

# 创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差。
# different nets
net_SGD         = Net() # create a neural network with Stochastic Gradient Descent optimizer
net_Momentum    = Net() # create a neural network with Momentum optimizer
net_RMSprop     = Net() # create a neural network with RMSprop optimizer
net_Adam        = Net() # create a neural network with Adam optimizer
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
# 4种常用的优化器
opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR) # create a SGD optimizer
opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8) # create a Momentum optimizer
opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9) # create a RMSprop optimizer
opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99)) # create an Adam optimizer
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss() # create a mean squared error loss function
losses_his = [[], [], [], []]   # used to save loss values
# 训练/出图
# training
for epoch in range(EPOCH):print('Epoch: ', epoch)for step, (b_x, b_y) in enumerate(loader): # train 4 models with different optimizers and save the results for printing# 对每个优化器, 优化属于他的神经网络for net, opt, l_his in zip(nets, optimizers, losses_his):output = net(b_x) # get the output of each networkloss = loss_func(output, b_y) # calculate the loss of each networkopt.zero_grad() # clear the gradients of the previous iterationloss.backward() # backward propagation, compute gradientsopt.step() # update parametersl_his.append(loss.data.numpy()) # save the loss
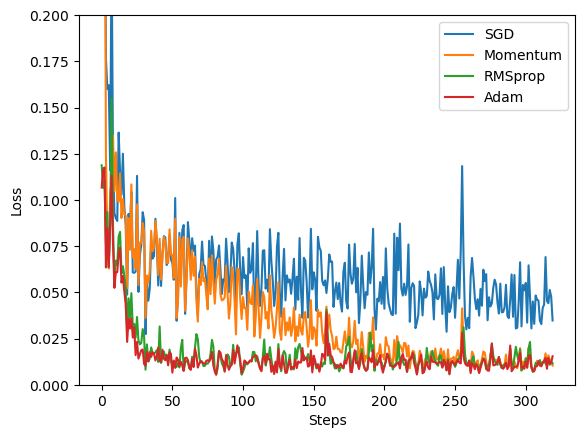
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()

Epoch:  0
Epoch:  1
Epoch:  2
Epoch:  3
Epoch:  4
Epoch:  5
Epoch:  6
Epoch:  7
Epoch:  8
Epoch:  9