笔记：代码随想录

概述

定义

满二叉树：一颗二叉树只有度为0和度为2的结点，度为0的结点在同一层上。

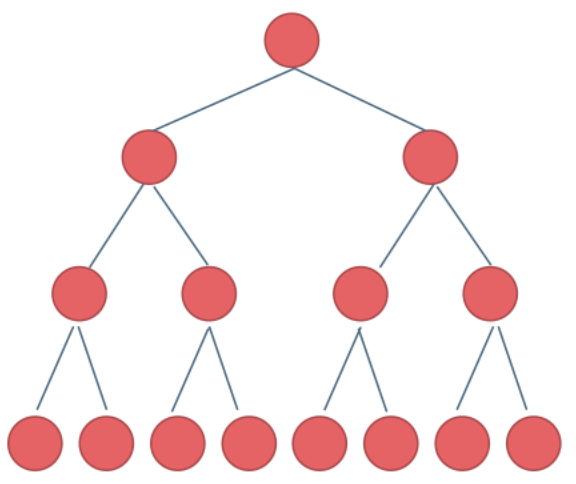
 完全二叉树：除最后一层不满，其余层都满，且有左到右的顺序。

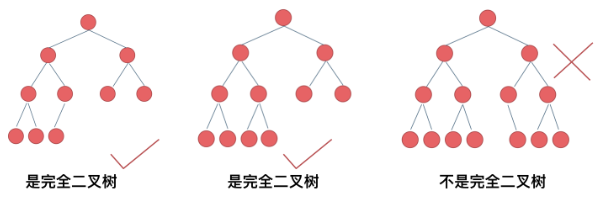
二叉搜索树BST：左小右大，对结点布局没有要求。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉排序树

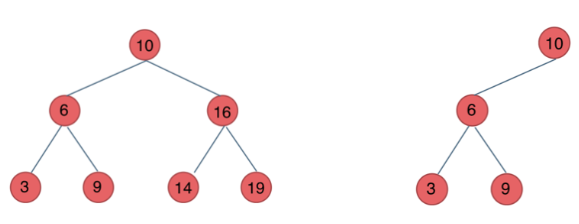
平衡二叉搜索树：空树或子树高度差不超过1。

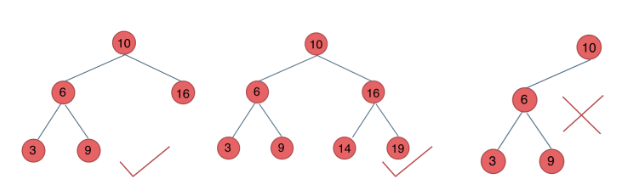
 二叉树存储方式：链式存储和线式存储。

链式存储方式就用指针， 顺序存储的方式就是用数组。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）

二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

其他

优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，unordered_map、unordered_set，unordered_map、unordered_set底层实现是哈希表。

方法

遍历

深度优先遍历：先往深走，遇到叶子节点再往回走（叶子节点是指没有子节点的节点）。前中后。【递归遍历】【迭代遍历】【统一迭代遍历】。

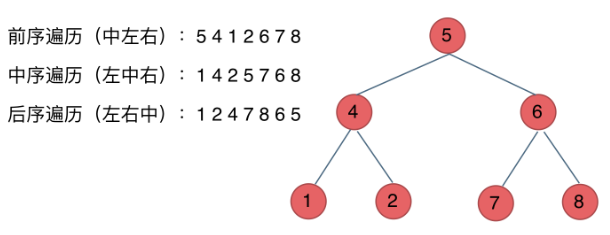
 广度优先遍历：一层一层的去遍历。【层序遍历】。

递归法三部曲

（1）确定递归函数参数和返回值。

（2）确定终止条件（就要确定节点为空的情况，否则就会操作空指针）。

（3）确定单层递归逻辑。

力扣

遍历

1.递归遍历

2.迭代遍历

前后序遍历稍作修改即可，中序遍历大改。这是与递归写法的区别。

3.统一迭代法

4.层序遍历

5.翻转二叉树

深度/高度

6.对陈二叉树

后序遍历：左右中，右左中

迭代法使用队列，栈或数组等容器实现，如果是模拟前中后序遍历就用栈，如果是适合层序遍历就用队列，当然还是其他情况，那么就是先用队列试试行不行，不行就用栈。

7.二叉树的最大深度

前序遍历和后序遍历：前序求深度，后序求高度，可利用后序求根节点高度来求深度。

8.二叉树的最小深度

求二叉树的最小深度和求二叉树的最大深度的差别主要在于处理左右孩子不为空的逻辑。

9.平衡二叉树

10.二叉树的所有路径

前序遍历：根节点到叶子节点。

遍历及深度，二叉树返回值的不同应用。构造二叉树

11.左叶子之和

节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

后序遍历：要通过返回值类加来求左叶子数值之和。

12.找树左下角的值

中序遍历/后序遍历都可：保证左优先，并且没有中间节点的处理逻辑，所以二者均可。

层序遍历喜欢的题。

13.路径之和

前中后序均可：无中间节点的处理逻辑。

递归函数返回值的判断。

• 如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
• 如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。 （这种情况我们在236. 二叉树的最近公共祖先
• (opens new window)中介绍）
• 如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

14.从中序与后序遍历序列构造二叉树

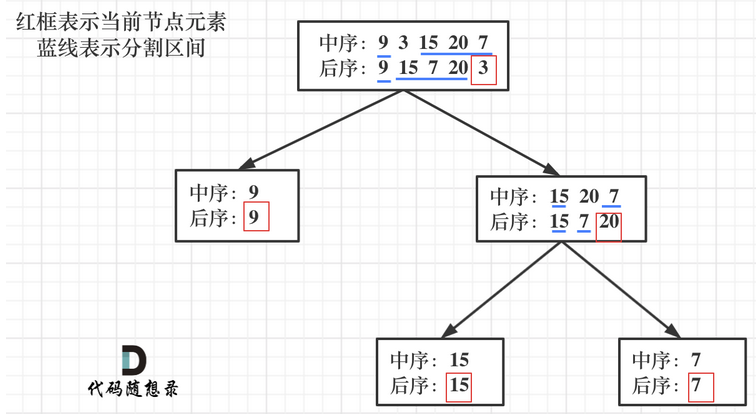
 15.最大二叉树

 前序遍历：因为先构造中间节点，再递归构造左子树和右子树。

二叉搜索树的综合应用

一般用中序遍历，因为可以形成排序好的数列。

16.合并二叉树

前中后序遍历：不涉及中间点逻辑。

17.二叉搜索树中的搜索

18.验证二叉搜索树

中序遍历：输出的节点数值为有序序列。

19.二叉搜索树的最小绝对差。

中序遍历

20.二差搜索树中的众数

21.二叉树的最近公共祖先

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

后序遍历：自底向上，天然的回溯过程。

二叉搜索树的综合应用（二）

22.二叉搜索树的最近公共祖先

前中后序：不涉及中间节点处理逻辑。

23.二叉搜索树中的插入操作

遍历整颗树就是对搜索树的侮辱。

24.删除二叉搜索树中的插入操作

25.修剪二叉搜索树

可以理解为：当不满足条件时，代码直接对树进行返回，而不接本层的值。

26.将有序数组转化为二叉搜索树

27.把二叉搜索树转化为类加树

反中序遍历