1. 概述

在这一章中，我们将解释如何使用 Alloy 来探索文件系统的设计。本章的目标是介绍 Alloy 的关键概念，即签名字段的概念，所以我们的例子将特意简单，是一个真实文件系统的非常高级的抽象。我们将只关注设计的结构方面，即我们的主要目标是描述文件和目录是如何组织的。

考虑到高度的抽象性，我们的结构规范将类似于领域模型，正式描述文件系统的概念和它们的关系。这个设计探索的另一个目标是引出一组约束条件，这些约束条件是一个完善的文件系统的特征。如果以后我们开发一个更详细的文件系统规范，即它的操作，这些将是我们想要验证的保持不变的约束。我们的最终目标将是验证这套约束条件是否包含文件系统的其他相关属性。特别是，我们对验证文件系统中没有分区的属性感兴趣，这意味着所有文件和目录都可以从根目录中访问。

2. 签名声明 Signature declaration

首先，我们将声明签名来捕捉文件系统中的概念：目录和文件。正如我们在前一章中所看到的，签名是一个集合，它将我们领域的一些元素组合在一起。由于文件和目录都有一些共同的属性，即它们都可以出现在一个目录中，所以在一个包含所有文件系统对象的顶级签名中声明各自的签名是很方便的。为了声明一个顶层签名，我们使用关键字 sig，后面是签名名称和大括号之间的字段声明列表。目前我们不会声明字段，所以一个包含所有文件系统对象的签名可以简单地声明如下。

sig Object {}

要声明一个子集签名，应该在签名名称后面使用关键字 in，然后是包括（或父）签名的名称。例如，包含目录和文件的 Object 的两个子集签名可以被声明如下。

sig File in Object {}
sig Dir in Object {}

在 Alloy 中，我们通常在规范过程的早期就开始验证一个设计，当时规范还很不完整。我们的目标是尽早发现设计问题或规范错误，而不是让它们积累到调试变得非常困难的程度。例如，我们可以立即使用 run 命令来查看我们的规范到目前为止的一些实例。

run example {}

这个命令可能返回的第一个实例是下面这个。回顾一下，一个实例是对签名（和字段，当规范也声明了这些字段时）的估值，它满足所有指定的约束，包括 run 命令中大括号之间的公式。一对空的大括号等同于真，所以在这种情况下，我们的签名没有受到任何约束。

这里我们有两个对象，其中一个是目录，另一个是文件。如果我们在可视化工具条上按下 "New"，我们可以得到以下实例。

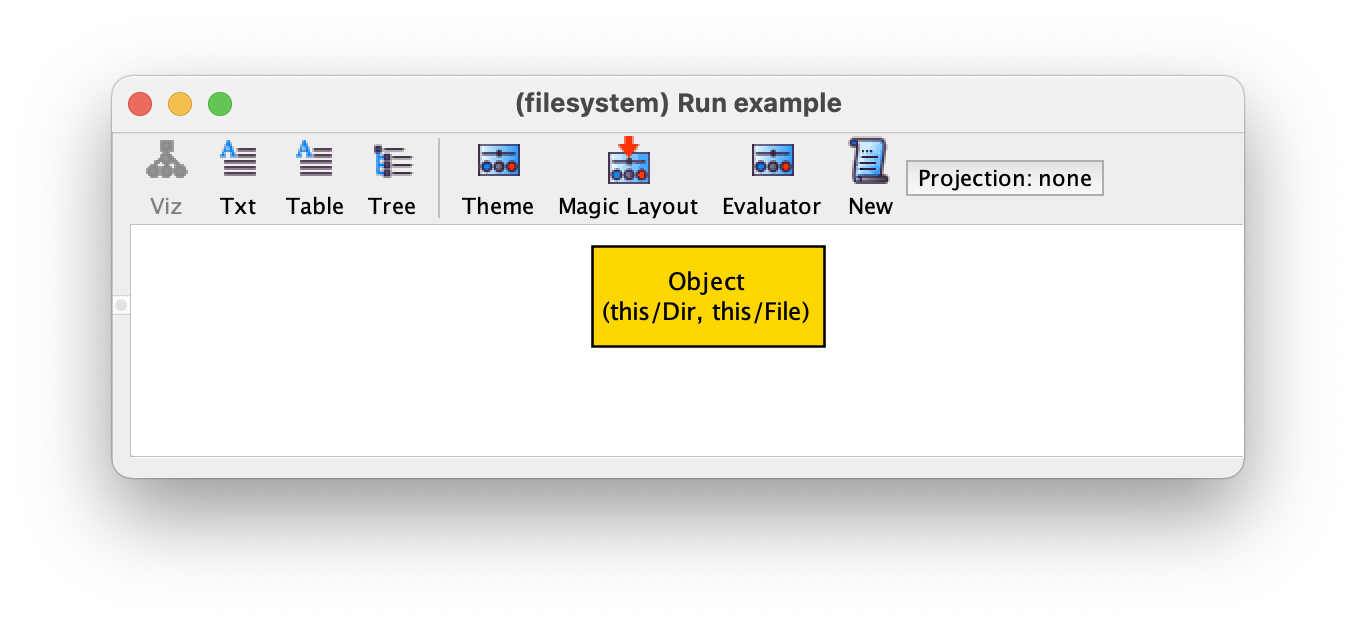
在这个例子中，我们有一个单一的对象，同时是一个目录和一个文件。很明显，这不是我们想要的，但当然它是允许的，因为 File 和 Dir 都是 Object 的任意子集。为了禁止这种情况，我们可以添加一个约束，禁止一个对象既是文件又是目录，方法是指定 File 和 Dir 是不相交的集合。为了在我们的规范中强加这个约束，我们可以在一个事实中指定它，如下所示。

fact { no File & Dir }

回顾一下，  & 表示集合相交，不检查集合的空性。

如果我们重新执行这个 example 的命令，并使用 "New "遍历我们的实例，我们将不再看到既是文件又是目录的对象，但我们最终会得到如下的实例，我们有一个对象（Object0）既不是文件也不是目录的问题。

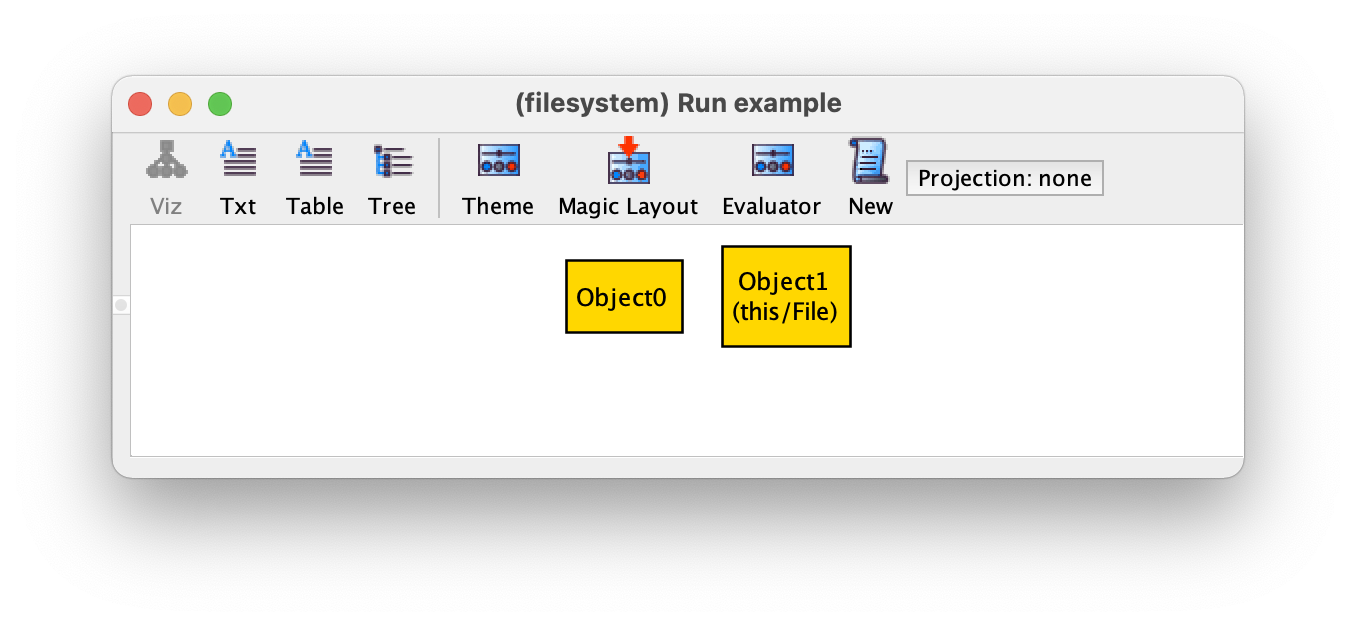
为了解决这个问题，我们可以给我们的事实添加另一个约束，要求 Object 只包含 File 或 Dir 中的原子，方法是要求 Object 是两者的联合（记得 + 表示集合的联合，事实内部不同行中的约束是隐含的连在一起的）。

fact {no File & DirObject = File + Dir
}

通过重新执行 example 命令并迭代实例，我们现在可以确认之前的问题已经解决了。

要求一些子集签名是不相干的，这是非常常见的。Alloy 有一个特殊的语法来声明这些：在签名声明中应该使用关键字 extends 来代替 in。例如，为了将 File 和 Dir 作为 Object 的两个不相交的子集，我们应该这样声明。

sig File extends Object {}
sig Dir extends Object {}

我们事实中的第一个约束现在是多余的，可以被删除。实际上，我们可以尝试通过发出下面的 check 命令来检查它确实是多余的，应该不会产生反例。回顾一下，check 命令验证了在指定的范围内，大括号之间声明的公式是由声明的事实所暗示的。如果不是这样，我们将得到一个反例，即事实成立但要检查的公式不成立的例子。

check { no File & Dir }

当执行这个命令时，我们实际上得到了一个警告：Analyzer 拒绝执行这个命令，并告诉我们，& 运算符是不相关的，因为它试图相交的两个子表达式是不相交的。这是由Alloy的类型系统发出的警告，也是使用 extends 来声明不相交的子集签名，而不是依赖 in 和额外的事实的优势之一。Alloy 的类型系统的主要目标是找到所谓的不相关表达式，基本上是分析器确信总是表示空集的表达式，因此最可能是用户所做的规范错误。如果用户确实想写一个总是表示空集的表达式，应该使用特殊的常量 none 来代替，以明确表示这一意图。

使用 extends 的另一个好处是，在可视化工具中，原子将根据它们所属的最具体的签名来命名，这简化了对 example 的理解。例如，由示例命令返回的一个可能的实例如下，现在更清楚的是我们有两个文件和一个目录。

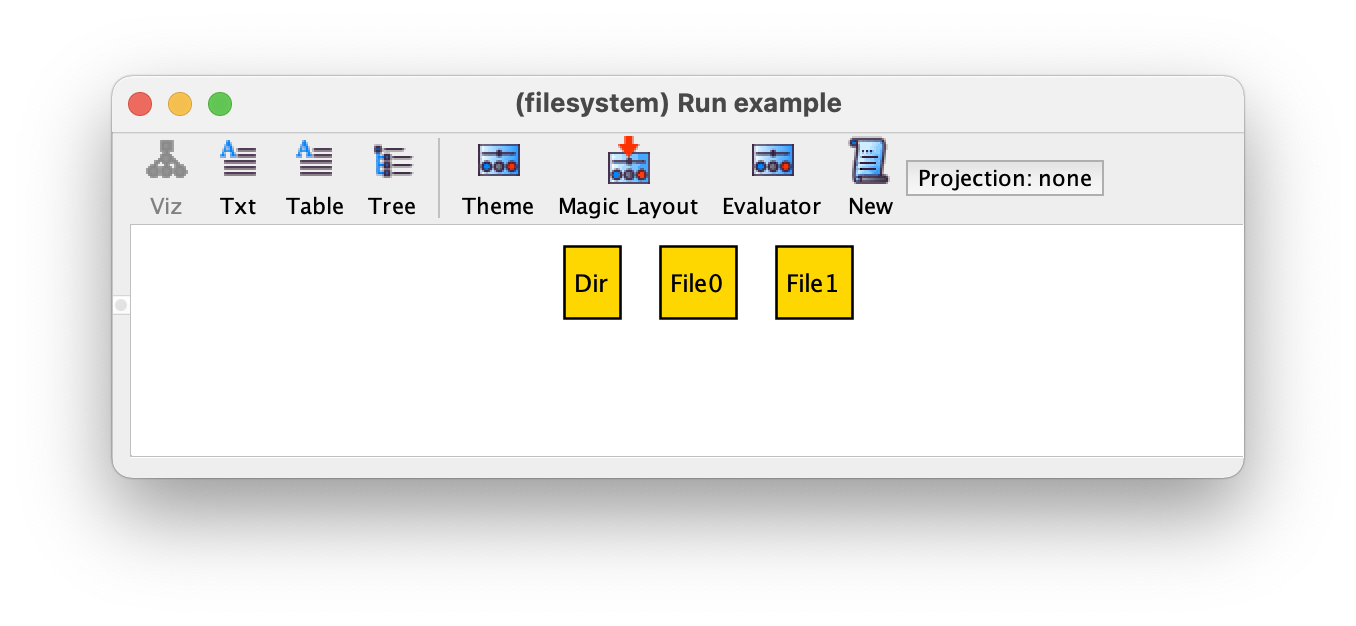
对扩展签名的另一个常见要求是，它们构成了父签名的一个分区。这就是签名 Object 的情况，它被分割成两个集合，即 File 和 Dir，并且除了已经包含在其扩展中的原子外，不包含其他原子。同样，与其像我们在约束 Object = File + Dir 时那样添加事实来确保这一点，不如在签名的声明前面加上关键字 abstract，这样就可以把签名声明为抽象的（abstract）。因此，我们对文件系统对象的规范可以如下，不需要任何额外的事实。

abstract sig Object {}
sig File extends Object {}
sig Dir extends Object {}

现在我们想添加一个特殊的对象来表示作为文件系统根的目录。在 Alloy 中，不可能在规范中直接引用（和命名）inhabit signatures 中的原子。但是有一个技巧可以做到这一点。签名声明前面可以有一个倍数约束（multiplicity constraint），限制该签名的 cardinality。有三种倍数可以用在签名声明中：some 强制签名总是有一些原子；lone 限制签名最多有一个原子；one 限制签名正好有一个原子。为了让根目录有一个特定的原子，我们可以用多重地（multiplicity） one 声明一个扩展了 Dir 的签名 Root。

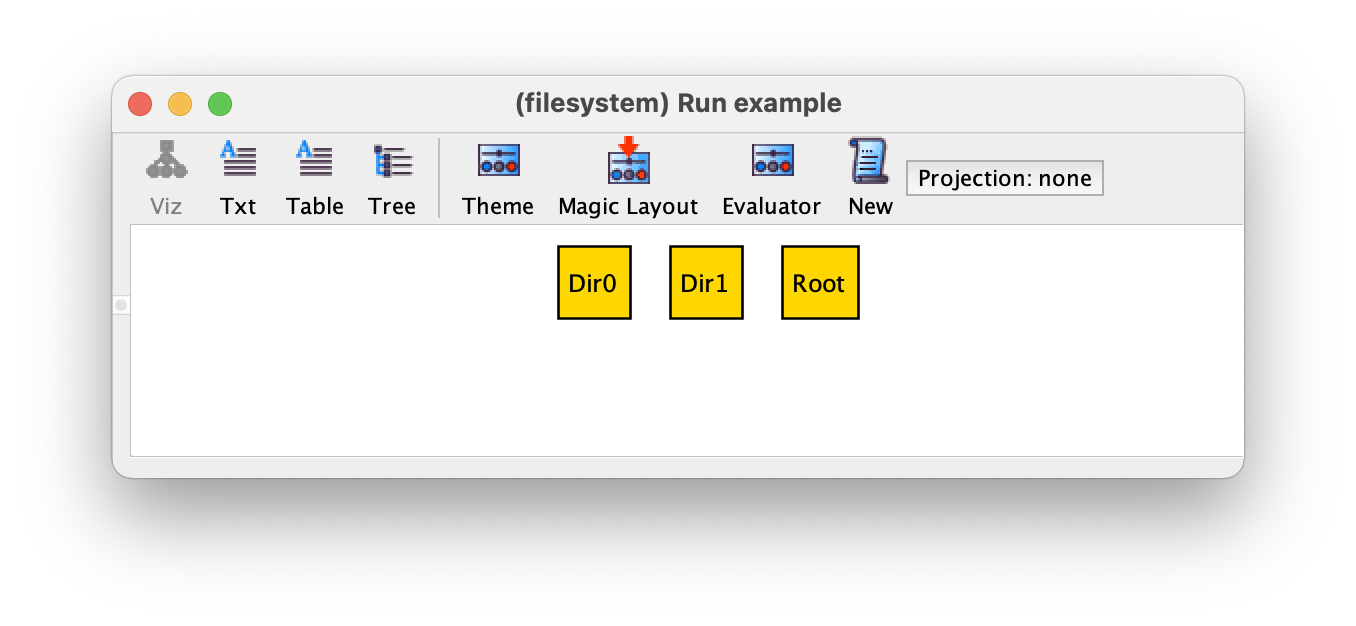
one sig Root extends Dir {}

Root 总是一个单子集，它包含文件系统根目录的原子。因为它是用 extends 来声明的，所以该原子在实例可视化中也将被命名为 Root。示例命令可能返回的实例如下，我们有三个目录，其中一个是（一定是）根目录。

Tip - 枚举签名 Enumeration signatures

在 Alloy 中，在声明签名时使用倍数为 one 的扩展签名是非常常见的，其行为类似于枚举数据类型。例如，下面的规范声明了一个正好包含三种颜色的 Color 签名： Red, Green, and Blue。

abstract sig Color {}
one sig Red, Green, Blue extends Color {}

这里我们看到 Alloy 语言的另一个特点：如果两个或多个签名有相同的特征（多重性、父签名等），它们可以在同一个声明中一起定义。

这种声明本质上对应于枚举数据类型的签名的模式非常普遍，Alloy有一个关键词  enum  用于此目的。使用这个关键字，Color 签名可以被声明如下。

enum Color { Red, Green, Blue }

然而，用关键字 enum 声明枚举签名和用普通的 sig 关键字声明倍数为 one 的枚举签名之间有一个微妙的区别：前者在各自的原子之间施加了一个总顺序，与它们在大括号内声明的顺序相对应。稍后我们将看到如何在Alloy中使用总顺序。

However, there is a subtle difference between declaring enumeration signatures with keyword enum and with the normal sig keyword with multiplicity one: the former additionally imposes a total order between the respective atoms, corresponding to the order in which they are declared inside the braces. Later we will see how total orders can be used in Alloy.

Objects inside directories have an associated name, so we will need a signature to represent the latter. In our file system model we will allow files to be (hard) linked, meaning that the same file can have different names in different directories (or even inside the same directory). As such, we will also introduce a signature Entry that will later be used as a (kind of) record to pack together an object inside a directory and the respective name.

sig Entry {}
sig Name {}

Note

Why not just use strings for names!?

The reader may wonder if Alloy has any predefined types, such as integers or strings. If that is the case, why not just use strings to represent names, instead of declaring a new signature Name? Actually, Alloy does have predefined types, namely Int for (bounded) integers and String for strings. However, these types should be avoided as much as possible, because their semantics is substantially more tricky than that of normal signatures, and analysis can be confusing and somehow crippled when using them (in particular with strings). Actually, in many cases they just have too much semantics for the intended use: for example, strings can be concatenated and there is the notion of one string being a substring of another, but the file system specification none of this is of interest when specifying the abstract concept of a name. The only thing we will need in this case is to check for name equality, and normal signatures and atoms already provide us that basic semantics. People also tend use integers when they actually need something much more simple, semantics wise. For example, we sometimes need to specify a signature where there is some total order imposed and, in first sight, integers are very convenient for that. However, integers have a more rich semantics than just being a total order, and we can easily axiomatise a total order on a signature with some simple facts and thus avoid the analysis drawbacks that come with their usage. So, when should you use String or Int? The former has very little use, and actually, even if recognised by the Analyzer, is not even part of standard Alloy. The latter is sometimes useful, for example when you do need to perform arithmetic operations, such as additions or subtractions.

A possible instance of our specification so far is the following, with two different names, two entries, one file and two directories, one of which is the root.

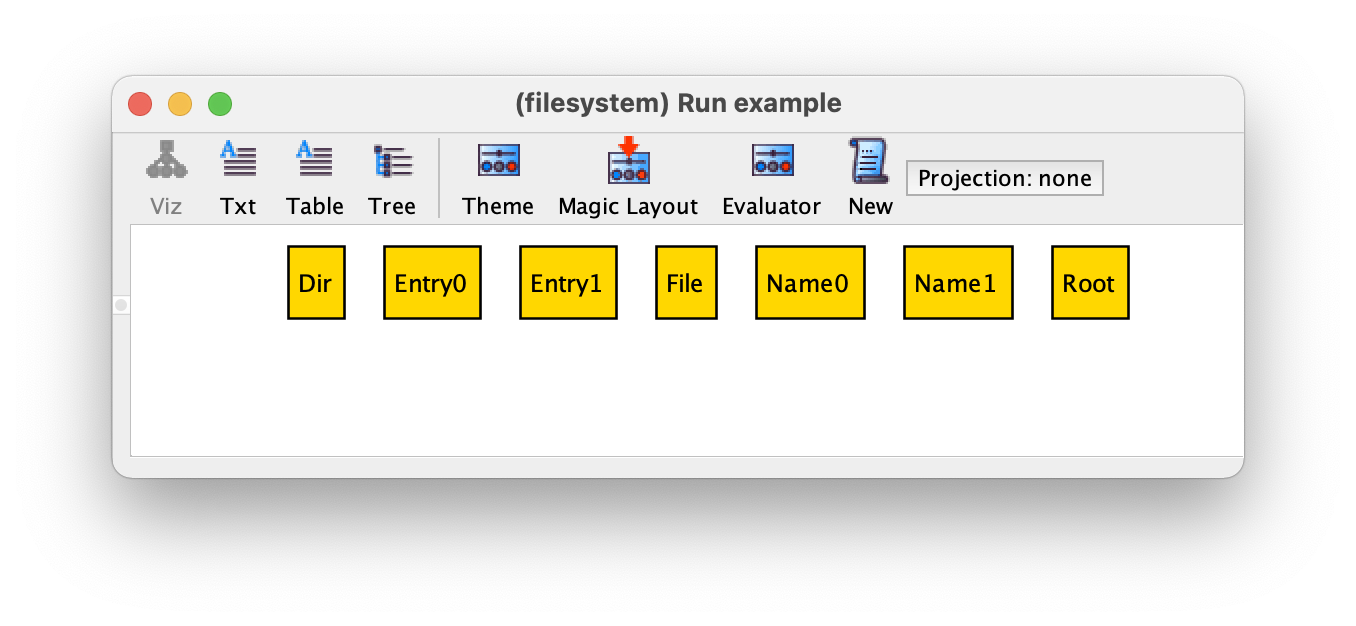
Recall that all analysis commands are executed with a (user definable) scope for each signature, that sets the maximum number of atoms that can inhabit it. By default, the scope is 3 for all top-level signatures: in our example this means that instances will have at most 3 names, 3 entries, and 3 objects. With this scope, instances with, for example, 3 files, will not be possible, because the root always exists and consumes 1 of the 3 atoms that can inhabit Object. To change the default global scope the keyword for followed by the desired scope should be used. You can also set a different scope for each top-level or extension signature (another difference from declaring signatures with in), by using the keyword but followed by a comma separated list with different scopes for each signature. You can also set an exact scope for a signature with the keyword exactly, meaning that that signature will always be inhabited by the exact number of specified atoms. For example, to execute the example command with a default scope of 4, up to 2 entries, and exactly 3 names, the scope should be set as follows.

run example {} for 4 but 2 Entry, exactly 3 Name

Note that in this case, the only top-level signature that will be subject to the default scope of 4 is Object, since specific scopes are given for the other two top-level signatures. Multiplicities on signature declarations also affect the scope: for example, a signature with multiplicity one will always have scope of exactly 1, and an error will be thrown if you try to set an incompatible scope. There is also some interaction between the scope of extension signatures and the scope of the respective parent signatures. In particular, if the scope of extension signatures enforces a minimum number of atoms, the scope defined for the parent signature will automatically grow to accommodate that minimum number. For example, in the following command the scope of Object will automatically grow to 4 since Object must contain at least the root and three files.

run example {} for 3 but 2 Object, exactly 3 File

Field declaration

Having declared our signatures we now proceed with the declaration of fields. Fields are declared inside the braces of a signature declaration, and are essentially mathematical relations (sets of tuples) that connect atoms of the enclosing signature to other atoms (of the same or other signatures). In our example we will need a relation that connects each directory with the respective set of entries. This binary relation, which will be named entries, is a set of ordered pairs, where the first atom of each pair is a directory and the second atom is an entry. The type of the first atoms in the tuples that form a relation dictates the signature in which it must be declared as a field. In the case of entries, since it relates atoms of signature Dir to atoms of signature Entry, it must be declared as a field in the former signature. To do so, we change the declaration of Dir as follows.

sig Dir extends Object {entries : set Entry
}

As we can see, a field declaration consists of its name followed by a colon and the target set, optionally preceded be a multiplicity declaration. In this case the target set is signature Entry and the multiplicity is set, meaning that one atom of signature Dir can be related by entries to an arbitrary number of atoms of signature Entry. The other options for the multiplicity are the same that can be used in signature declarations: one, lone, or some. If no multiplicity is given, the default is one. In this book we will avoid this implicit multiplicity in field declarations, and always explicitly state the multiplicity of a field, even if it is one.

By executing command

run example {}

we could now get the following instance.

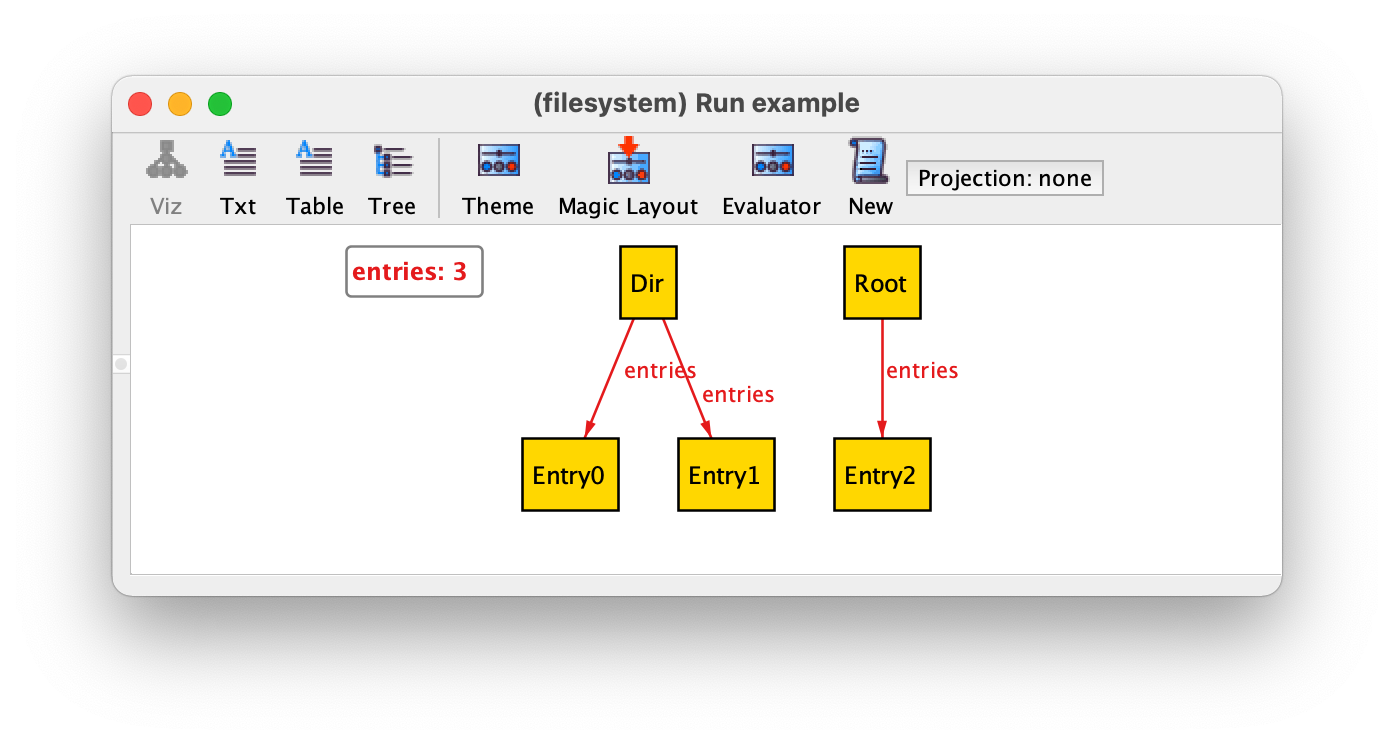
Binary relations are depicted by the Analyzer using labelled arrows: each arrow is a pair contained in the relation, whose first atom is the source of the arrow and whose second atom is the target. In this case, relation entries is a set that contains three pairs: (Dir,Entry0), (Dir,Entry1), and (Root,Entry2). In this example we have a directory Dir with two entries and the Root with one entry, but given the set multiplicity constraint it would also possible to have directories without any entries.

Note

Actually, everything is a relation!

In chapter An overview of Alloy we alerted the reader to the fact that in Alloy every expression denotes a set. To be more precise, every expression in Alloy denotes a relation - a set of tuples - hence the Alloy motto: everything is a relation! In Alloy we can declare relations of arbitrary arity: the arity is the size of the tuples contained in it. Relation entries is a binary relation of arity 2. Later we will see how to declare relations of higher arity, for example ternary relations of arity 3. However, signatures are in fact also relations of arity 1: they are sets of tuples of size 1. For example, in the previous instance, signature Dir contains the following unary tuples: (Dir) and (Root). Do not to confuse the name of the atom Dir with the signature name Dir: the former is just an automatically-generated name for one of the two inhabitants of the latter! When we start using relational logic operators to write constraints, it will be more clear why the fact that everything denotes a relation considerably simplifies the syntax and semantics of the language.

Tip

The evaluator.

The Alloy instance visualiser has an evaluator that can be used to compute the value of any expression. To access this evaluator just press the Evaluator button in toolbar of the instance visualiser window. Every expression denotes a relation. The visualiser depicts the values of the signatures and fields of an instance as labelled graphs. Another way to depict the value of a relation (of any arity) is as a table where each line is one of the tuples contained in it. This is the default way the evaluator will show the values of relational expressions. To ask for the value of an expression just type it in the evaluator and press Enter. For example, here is the result of asking in the evaluator what is the value of relations Dir and entries.

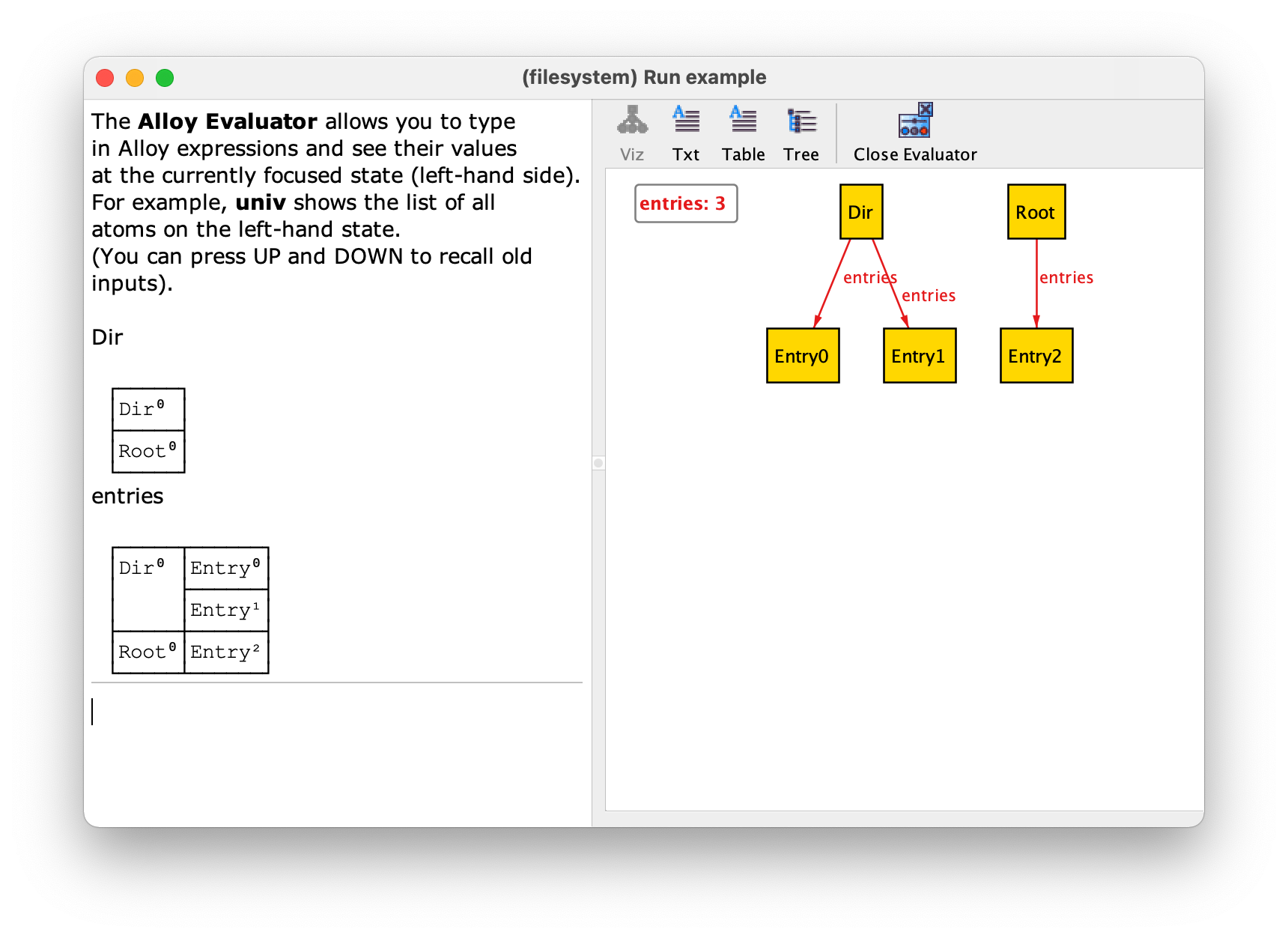
The evaluator is sometimes very useful to debug your constraints: besides asking for values of relational expressions you can also ask for the values of formulas, so it is a very convenient way, for example, to know what sub-formulas of a constraint are true or not in a particular instance. To close the evaluator and return to the normal instance visualizer just press the Close Evaluator button in the toolbar.

Besides entries we will declare two more fields in our specification: the first, that we will call name, relates each entry in a directory with the respective name; the second, that we will call object, relates each entry in a directory with the respective file system object (either a file or a directory). Both these relations should be declared inside signature Entry and both will have multiplicity one, since exactly one target atom is associated with each entry. Because of this, an entry acts like a record that packs together an object inside a directory and the respective name. In section Using higher-arity relations we will see how this association (between directories, their contents, and the respective names) can alternatively be modelled by a ternary relation.

sig Entry {name : one Name,object : one Object
}

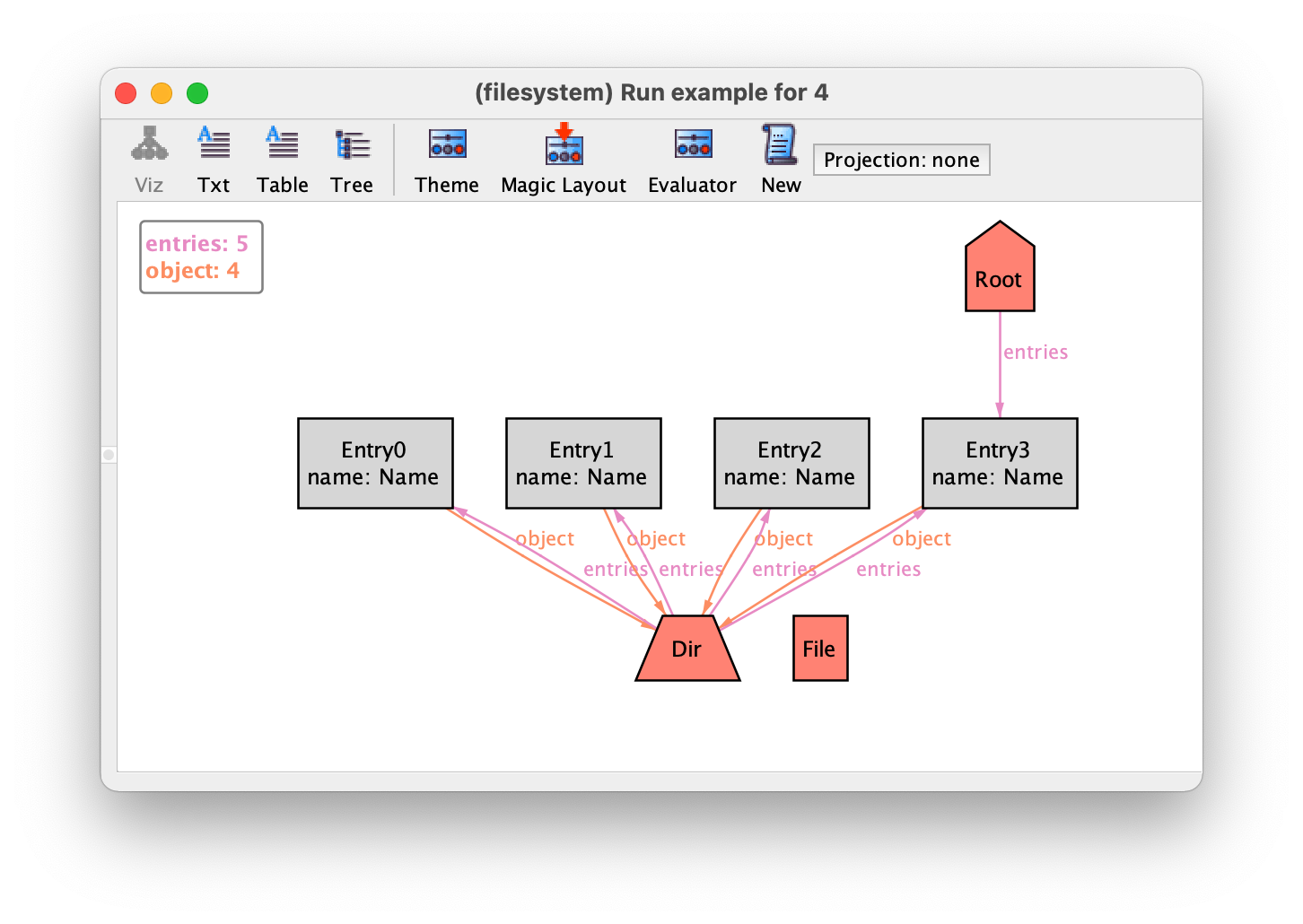
Let’s change our run command to ask directly for a more complex instance of our specification, namely one with a larger global scope of 4, and necessarily containing some files and some directories besides the root (recall that - is the set difference operator, and that keyword some, besides being used as a multiplicity constraint in declarations, can be used in formulas to check if a set (or relation) is non-empty).

run example {some Filesome Dir - Root
} for 4

Executing this command could yield the following instance.

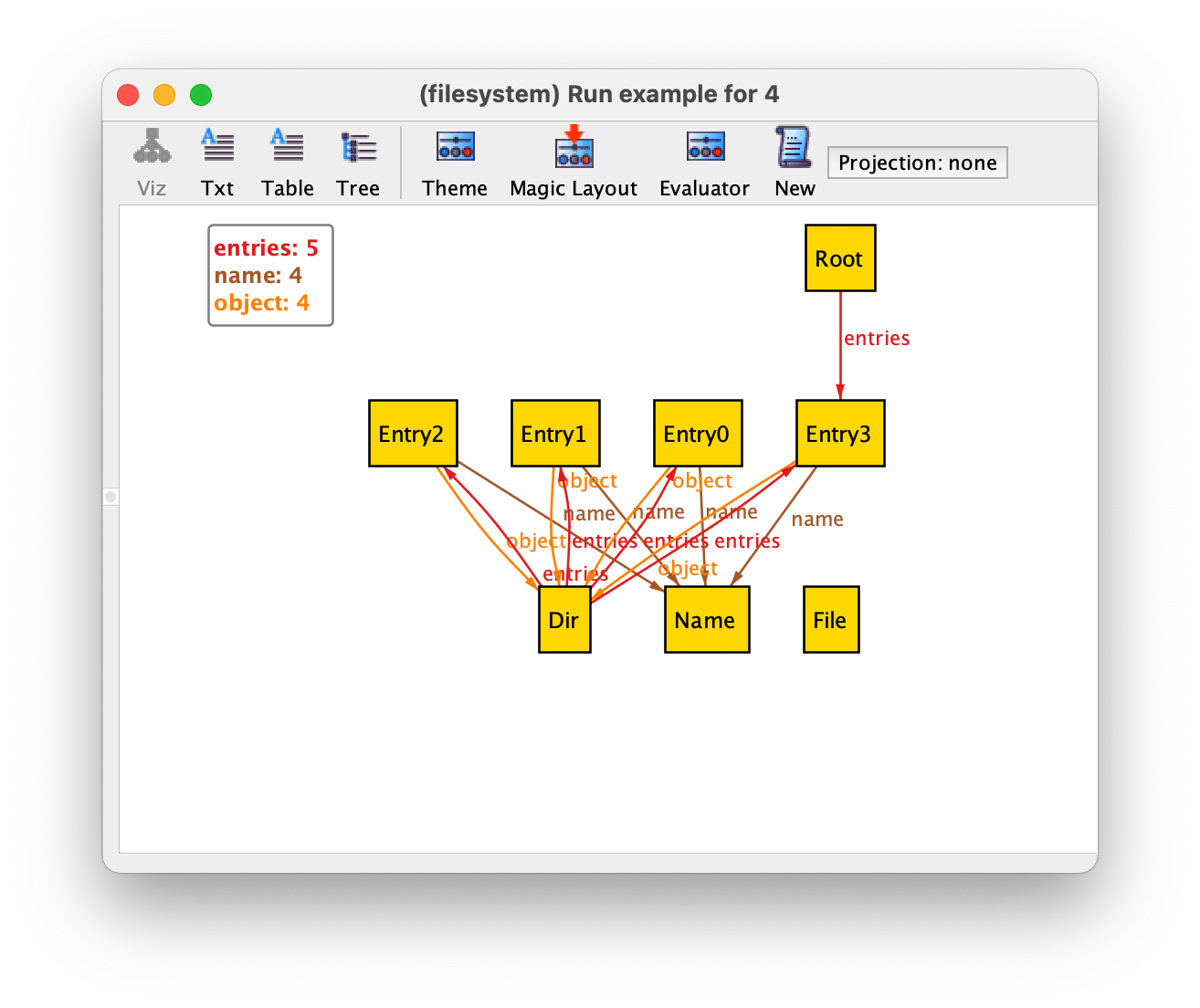
Here we can immediately see some problems with our specification, for example entries shared between directories or files not belonging to any directory. As our specification grows, instances become increasingly difficult to understand, and so, before adding facts to our specification to solve these issues, we will first see how the theme can be customised to simplify the visualisation of instances.

Theme customisation

To open the theme customisation menu, press the button Theme in the toolbar of instance visualiser window. The first customisation we will apply is to show the names of directory entries as attributes in the respective atoms, instead of using arrows pointing to the name. This will unclutter substantially the depiction and is a very common customisation for fields of multiplicity one, in particular for fields that somehow act as identifiers, as is the case of name. To do so, first select the field name, and then tick the Show as attribute option in the top pane. This option will show the name of an entry as an attribute but still keep the respective arrows. To remove them, tick twice Show as arcs to choose the Off option. Your theme options for relation name should look as follows.

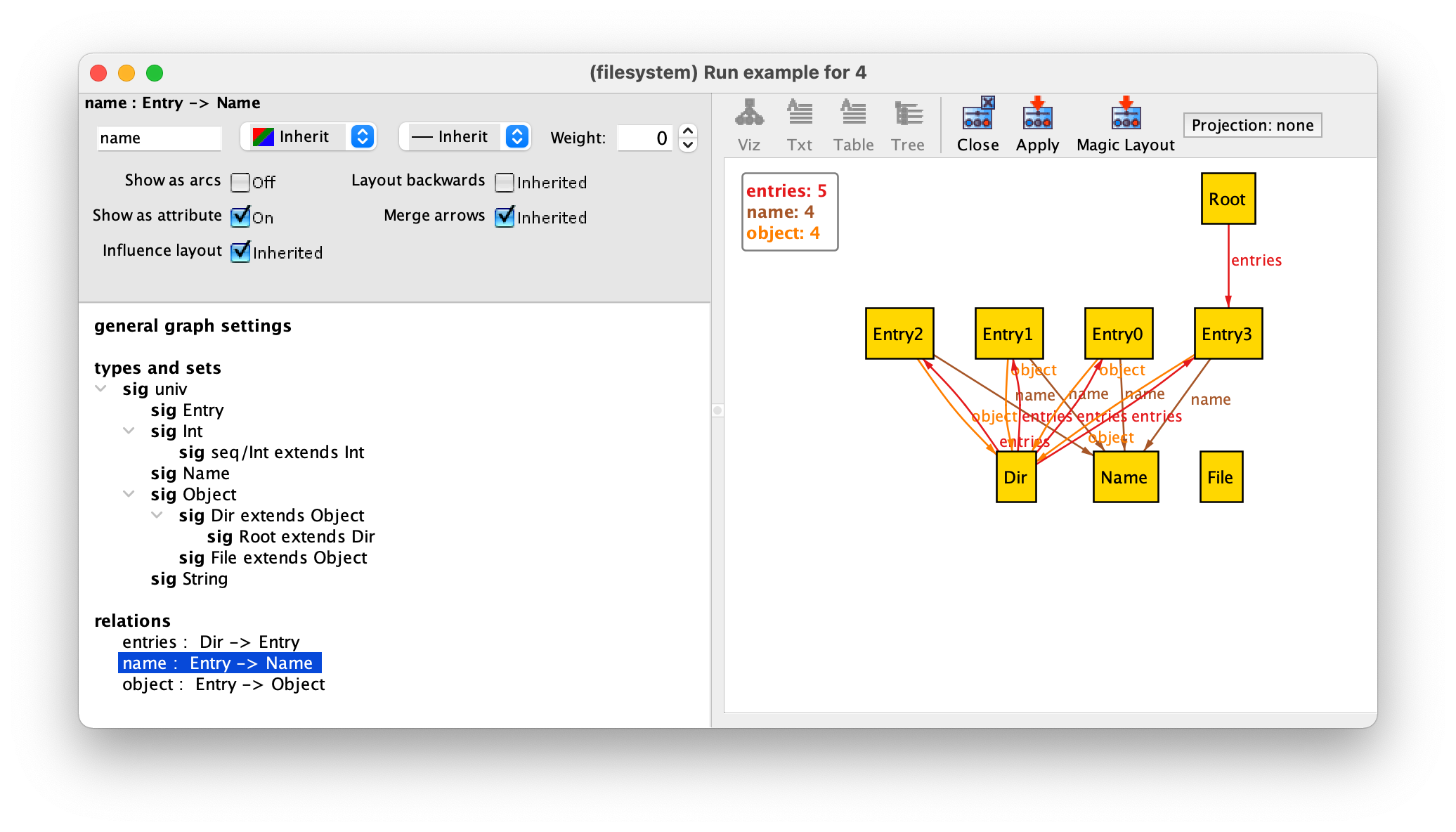
By pressing Apply in the toolbar and then Close the instance will now be depicted as follows.

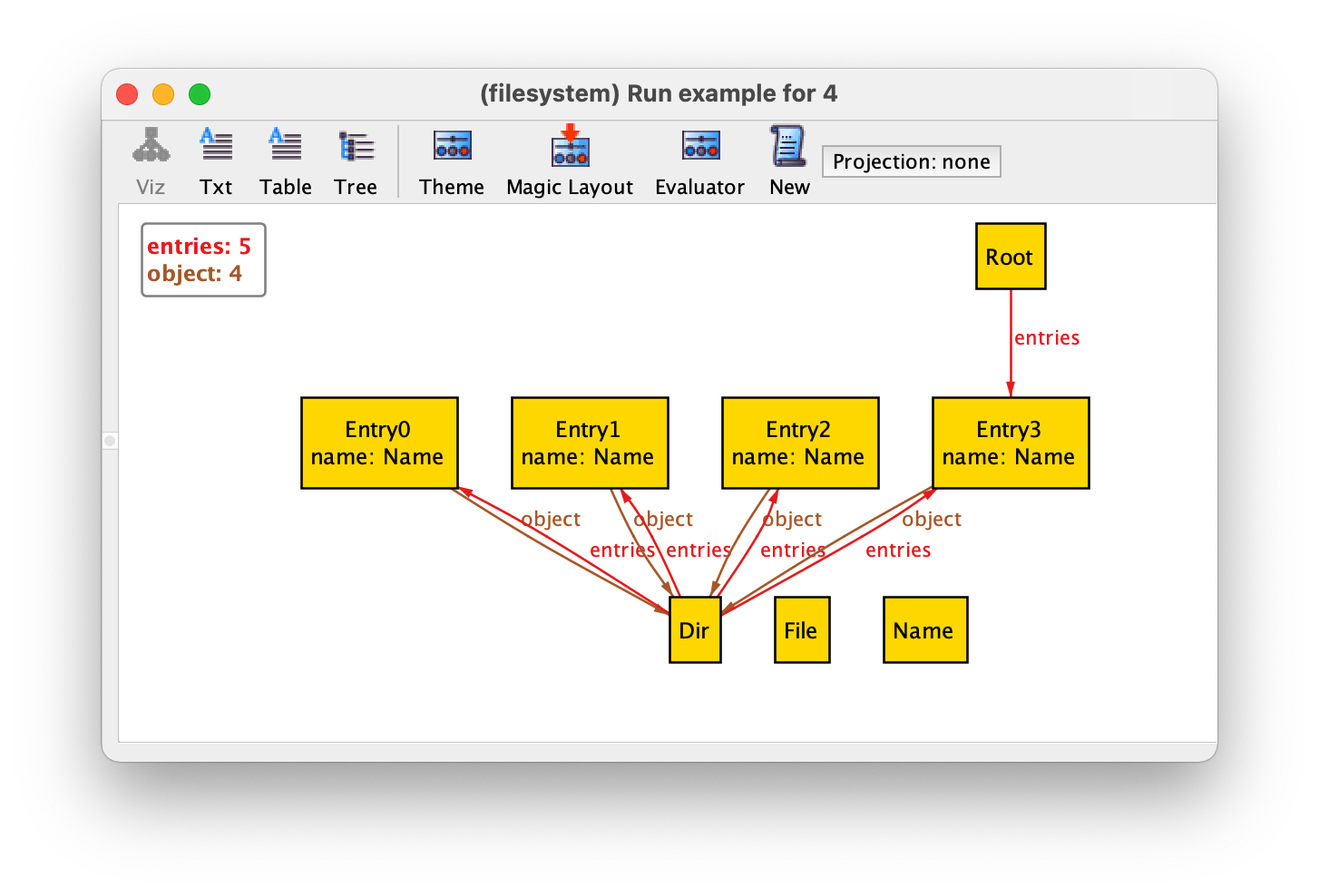
We now have some unconnected Name atoms. Since names were only used in directory entries, where they are now shown as attribute, we can remove them from the graph. To do so, select Theme again (actually when changing many options it is better to keep the theme customisation menu open and just keep pressing Apply without closing it to see the effect), select the Name signature, and then tick the Show option twice to choose the Off option. After pressing Apply the Name atom will disappear.

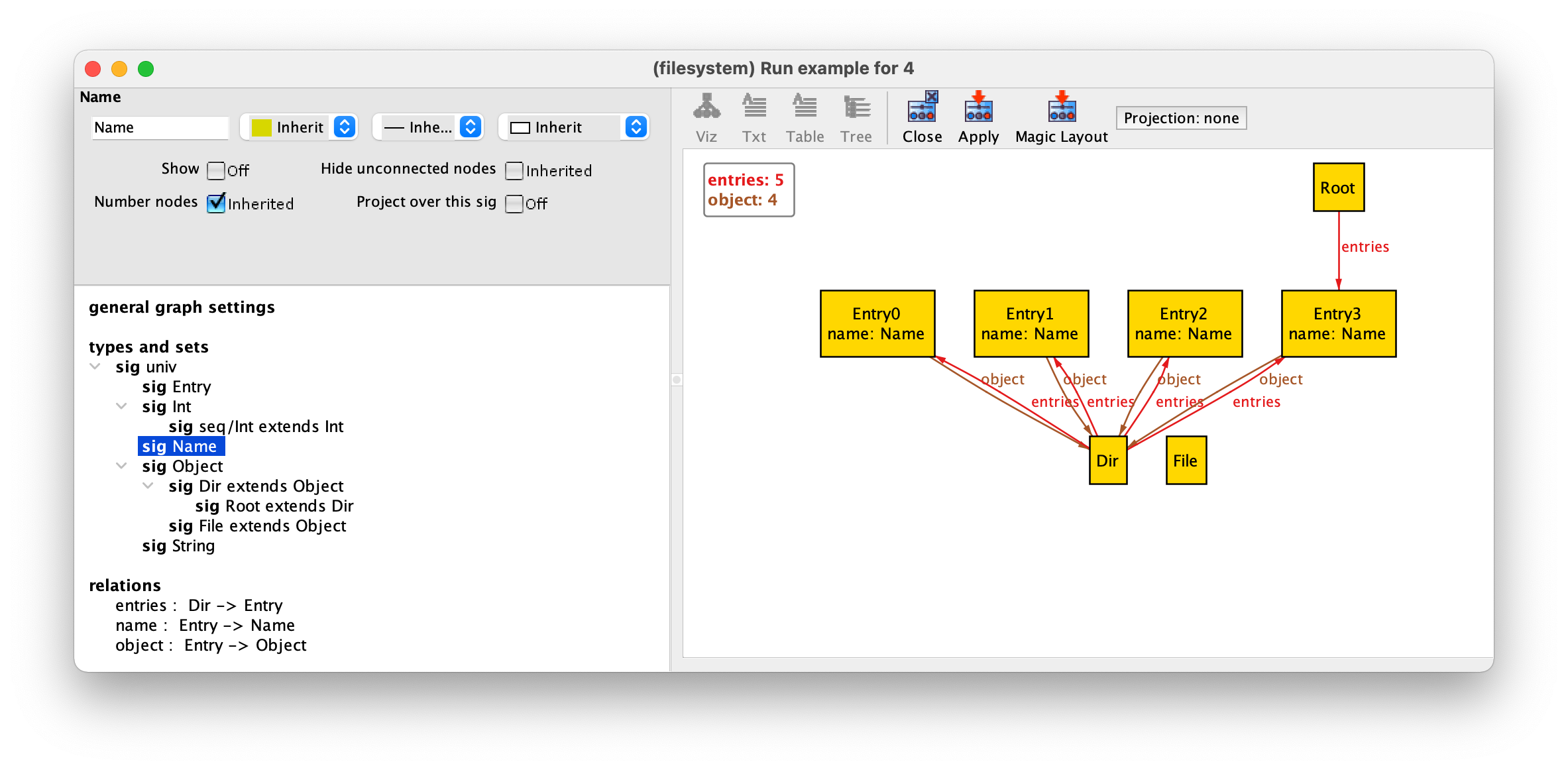
Another common customisation is to give different colours (or different shapes) to atoms belonging to different signatures. First, we will select a different colour palette, with more subdue colours. First select the general graph settings, and select the Martha (for Martha Stewart) palette both for node and edge colours. After pressing Apply we will get some nice faded colours.

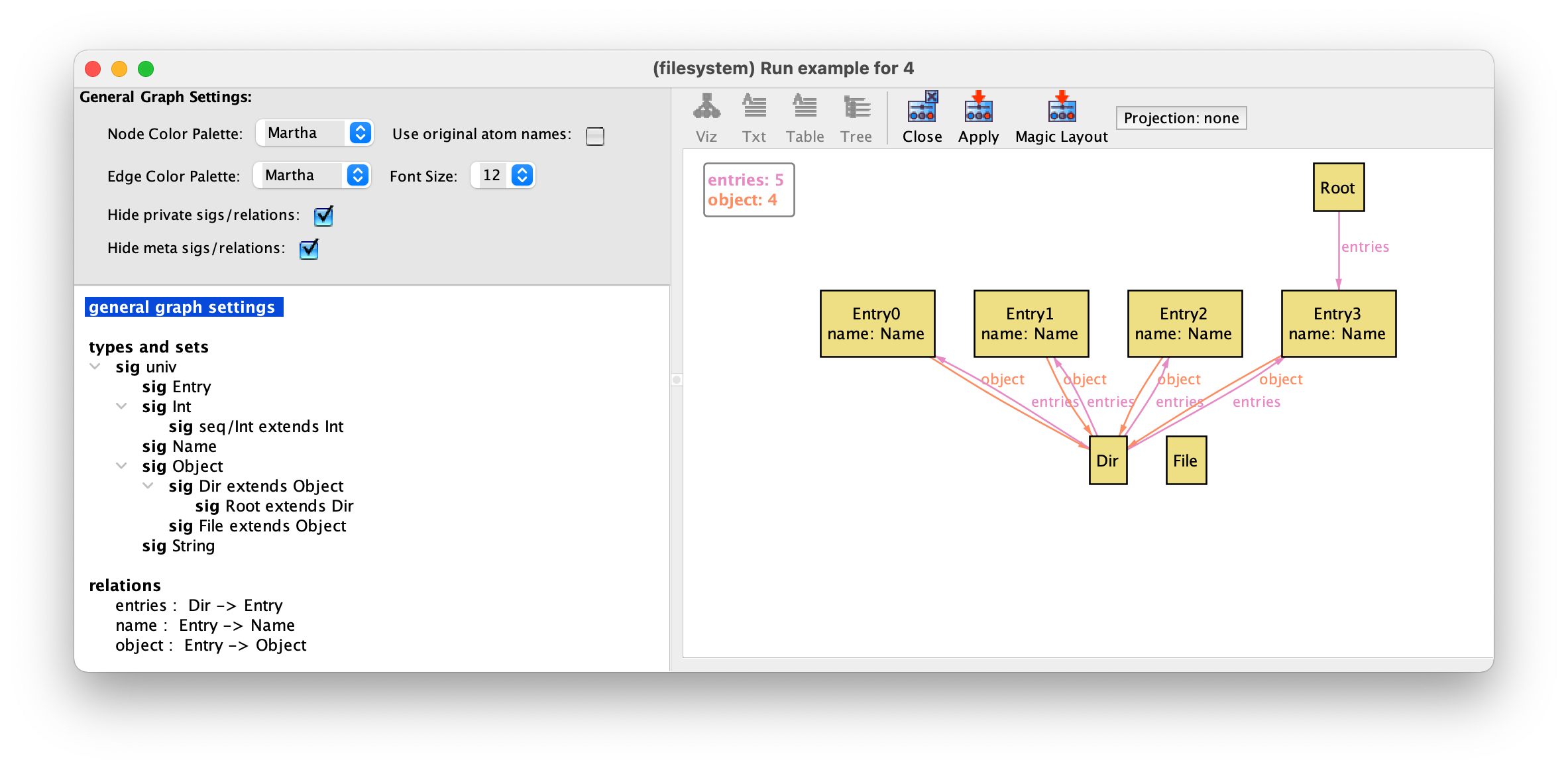
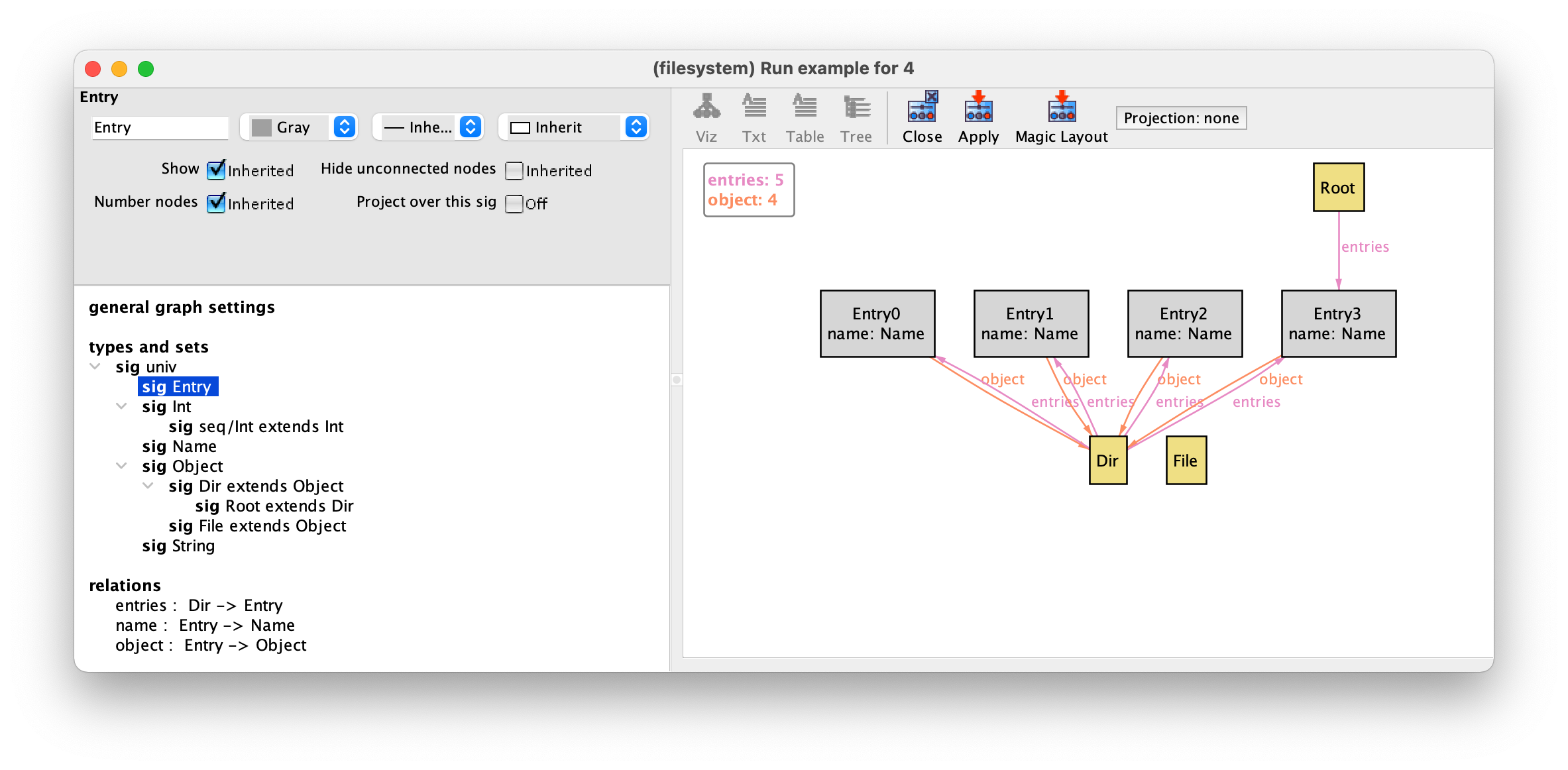
Since entries are auxiliary structures in defining the (supposedly) tree-like structure of the file system, we will paint them grey. To do so select signature Entry, then the colour Gray in the drop-down menu in the top left-hand corner, and finally Apply.

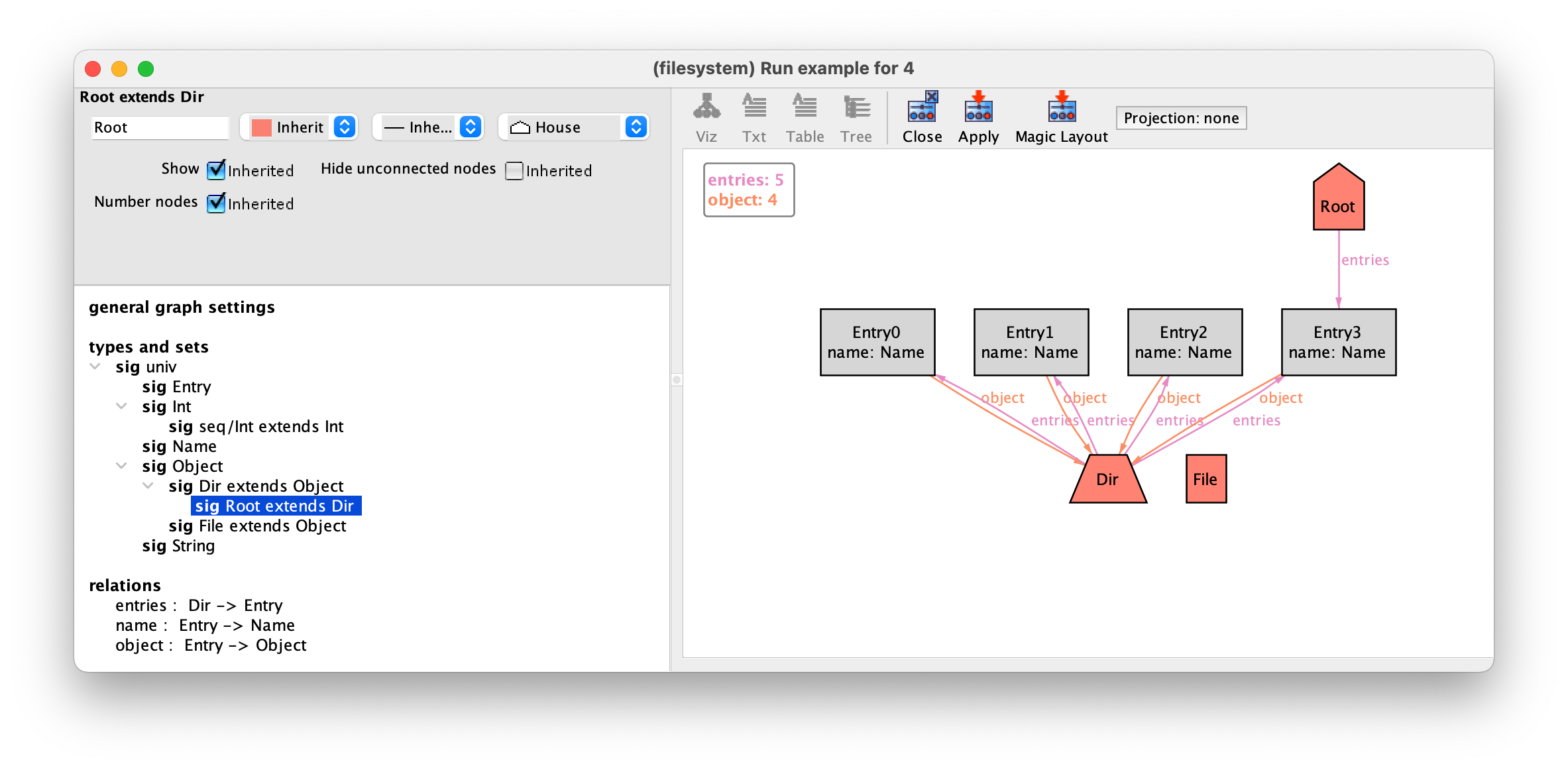
For file system objects we will choose a more eye-catching red colour. We don’t have to set this colour separately for Dir and File. By default most theme options of extension signatures are set as inherited from their parent signature. As such, it suffices to set the colour red for the Object signature, and both their children will inherit this setting. Finally we will choose different shapes for different file system objects. Let’s keep files as rectangles, but choose the shape Trapezoid for directories and a House for the root. The shape can be chosen in the drop-down menu in the top right-hand corner. After pressing Apply we have the following.

For the moment these are all the customisations we will use, and so we can close the theme customisation menu. Notice that you can always reset your theme settings by going to the menu option Theme ‣ Reset theme. You can also save your theme for later use in the option Theme ‣ Save theme. Instead of customising manually your theme, you can also try out the Magic Layout button in the toolbar of the instance visualiser. This will “magically” choose options for visualising the different elements of your specification: sometimes the results are good enough and it will save you some work. The result of magic layout for our instance is the following.

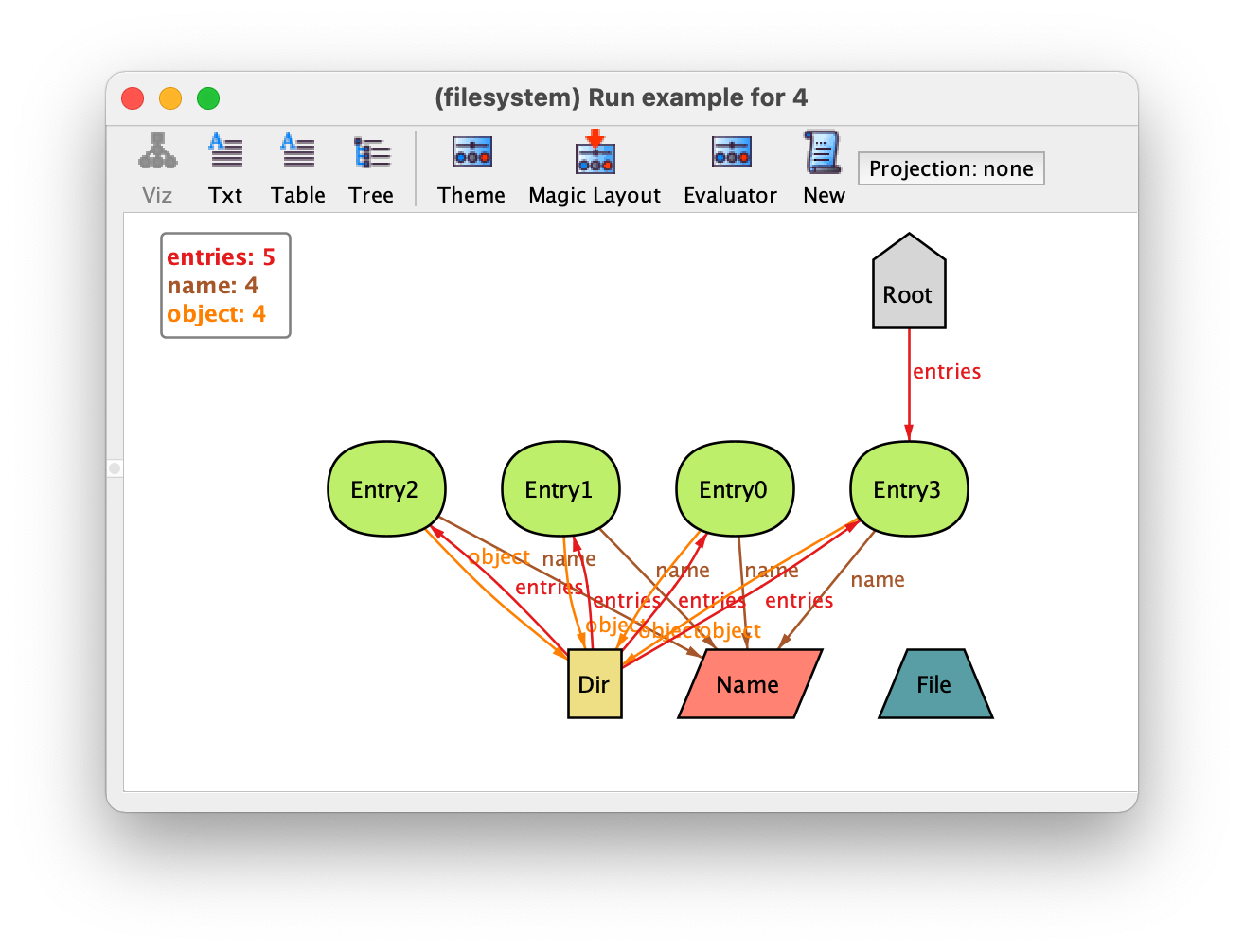
More information about how the magic layout actually works can be found in [LED07]. In this case we prefer our handmade customisation and so we will load back our previously saved theme by selecting Theme ‣ Load theme.

Property specification

By inspecting the above instance we can easily detect several problems in our specification, namely:

• Shared entries between directories (entry Entry3 belongs both to Dir and Root).

• Different entries in the same directory with the same name (all entries inside Dir have the same name Name).

• The same directory appears in more than one entry (Dir is the object of all entries).

• A file that does not belong to an entry (File)

We should write facts to prevent these issues. In Alloy, formulas in facts are written in a variant of first-order logic called relational logic. Relational logic extends first-order logic with so called relational operators, that can be used to combine (or compose) relations (which in first-order logic are known as predicates) to obtain more complex relations. We have already seen some of these operators, namely the classic set operators such as intersection (&), union (+), and difference (-). Notice that every relation (of any arity) is a set of tuples, so these can be applied to any relation. Let’s suppose, for example, we have two binary relations, mother and father, that relate a person with the respective mother and father. Then the relation that gives the parents of a person can be obtained by taking the union of both, namely mother+father.

The essential operator in relational logic is composition, the binary operator written as . (a dot). This operator allows us to navigate through the declared fields to obtain related atoms. Understanding how this operator works is key to be proficient in Alloy. Here, we will explain its informal semantics by means of several examples: the detailed semantics and more examples will be given in chapter A relational logic primer. In particular we will focus on the simplest, and most frequent, use of this operator, namely when applied to a set and a binary relation. For example, suppose e is a singleton set containing an Entry and d a singleton set containing a Dir. These could be, for example, parameters of a predicate or instantiated as result of a quantifier. To obtain the name of an entry you can compose it with relation name: relational expression e.name denotes the name of e. Since name is a field with multiplicity one, the result of this composition is necessarily a singleton set. Similarly, e.object is the singleton set with the file system object that is contained in entry e.

The notation is, on purpose, similar to that of accessing an attribute of an object in an object-oriented programming language, as the effect is essentially the same when dealing with singleton sets. However, we can also apply it to relations with multiplicity different than one and arbitrary sets. For example, d.entries retrieves the set of all entries in directory d. This set can be empty or contain an arbitrary number of entries, since relation entries has multiplicity set. A more interesting usage is when composing a non-singleton set with a relation. For example, Entry.name is the set of all names of all entries and Dir.entries is the set of all entries that belong to some directory. Also, you are not forced to compose a set followed by a relation: the other way around also works. Relations can be navigated forwards, from the source signature to the target signature, but also backwards from the target signature to the source one. For example, entries.e denotes the set of directories that contain entry e: this set can be empty, if e is not contained in any directory, or even have more than one directory, since when declaring a field there are no multiplicity restrictions imposed on the source signature. We can also compose with an arbitrary set on the right-hand side: for example, entries.Entry is the set of all directories that contain some entry.

Compositions can be chained to obtain atoms that are somehow indirectly related. For example, d.entries.object denotes the set of all file system objects that are contained in the entries of directory d. And again, it is possible to navigate backwards through composition chains. For example, entries.object.d denotes the set of all directories with entries that contain directory d.

Having understood how . works, we can now declare a fact that prevents the first issue identified above. We can almost directly transliterate the natural language requirement to relational logic. Given any two different directories x and y, the property that there should be no common entries between both can be specified as no (x.entries & y.entries): first we determine the intersection of the two sets of entries of both directories, and then we check that this set is empty using the keyword no. To complete our first property specification we just need to universally quantify over all different directories x and y (recall that all denotes the universal quantification of first-order logic).

fact {// Entries cannot be shared between directoriesall x,y : Dir | x != y implies no (x.entries & y.entries)
}

The need to quantify over two ore more different variables is very common, so Alloy provides the modifier disj, that can be added between the quantifier and the variables, precisely to restrict those variables to be different. This modifier simplifies the formulas, since we no longer need the implication to indirectly restrict the range of the quantification. Using this modifier, our property can be restated as follows.

fact {// Entries cannot be shared between directoriesall disj x,y : Dir | no (x.entries & y.entries)
}

As expected there are many different ways to specify the same property. In the case of this property, a simpler formula can be obtained by navigating backwards in the entries relation, and specifying instead that for every entry e there should be at most one directory in the set entries.e, the set of all directories that contain e as an entry. This alternative formulation would look as follows. Recall that lone can be used to check if a set contains at most one atom.

fact {// Entries cannot be shared between directoriesall e : Entry | lone entries.e
}

Alloy has a special formula syntax to directly restrict the multiplicities of both end points of a binary relation. For example, to state that a relation r relates every atom of source signature A to at most one atom of target signature B, and every atom of B to at least one atom of A, we could write the formula r in A some -> lone B. Not stating a multiplicity next to an end point is the same as having multiplicity set. With this special syntax, we could have yet another alternative formulation of our first constraint.

fact {// Entries cannot be shared between directoriesentries in Dir lone -> Entry
}

Note

A bestiary of binary relations.

The constraint entries in Dir lone -> Entry forces relation entries to be injective, one where no two atoms of the source signature point to the same target atoms. This is one of the four basic properties of relations we can obtain by varying the multiplicities of the source and target signatures. If we had entries in Dir some -> Entry we would have a surjective relation, one where every atom of the target is related to some source atom. If entries in Dir -> lone Entry relation entries would be simple (or a partial-function), a relation where every source atom is related to at most one target. And if entries in Dir -> some Entry relation entries would be entire (or total), since every source atom is related to at least one target. By combining these four properties we get additional well-known relation types. A relation that is both entire and simple is a function: every atom of the source is related to exactly one target. A representation is a relation that is both entire and injective, and dually, an abstraction is a relation that is both simple and surjective. An injection is a function that is also a representation, and a surjection is a function that is also an abstraction. Finally, by combining all four basic properties we get a bijection: a one-to-one mapping between the source and the target signatures. The following table summarises these properties.

injective	entire		simple		surjective
A lone -> B	A -> some B		A -> lone B		A some -> B
representation		function		abstraction
A lone -> some B		A -> one B		A some -> lone B
injection			surjection
A lone -> one B			A some -> one B
bijection
A one -> one B

To enforce that different entries in the same directory have different names we could write the following fact.

fact {// Different entries in the same directory must have different namesall d : Dir, disj x, y : d.entries | x.name != y.name
}

Here you can see another nice feature of Alloy’s syntax: it is possible to quantify over any expression and not only over signatures. In this case, x and y will be instantiated with all the (distinct) atoms belonging to d.entries, the set of entries of each directory d. An alternative formulation of this property is the following.

fact {// Different entries in the same directory must have different namesall d : Dir, n : Name | lone (d.entries & name.n)
}

Expression d.entries & name.n denotes the set of entries in directory d that also have name n. This set must contain at most one entry for every directory d and name n.

To prevent the third issue we can enforce that each directory is contained in at most one entry as follows.

fact {// A directory cannot be contained in more than one entryall d : Dir | lone object.d
}

Note that it would be wrong to specify this property as object in Entry lone -> Dir, since this would force relation object to only relate entries to directories (excluding files).

The last issue is a an example of a broader problem: there is nothing in our specification that forces all objects except the root to belong to an entry. To specify such a constraint, we can begin by determining the set of all objects that are contained in any entry using expression Entry.object, and then enforce that this set is equal the set of all objects minus the root.

fact {// Every object except the root is contained somewhereEntry.object = Object - Root
}

After adding these four facts, if we re-execute the example command and iterate with New we could get the following instance.

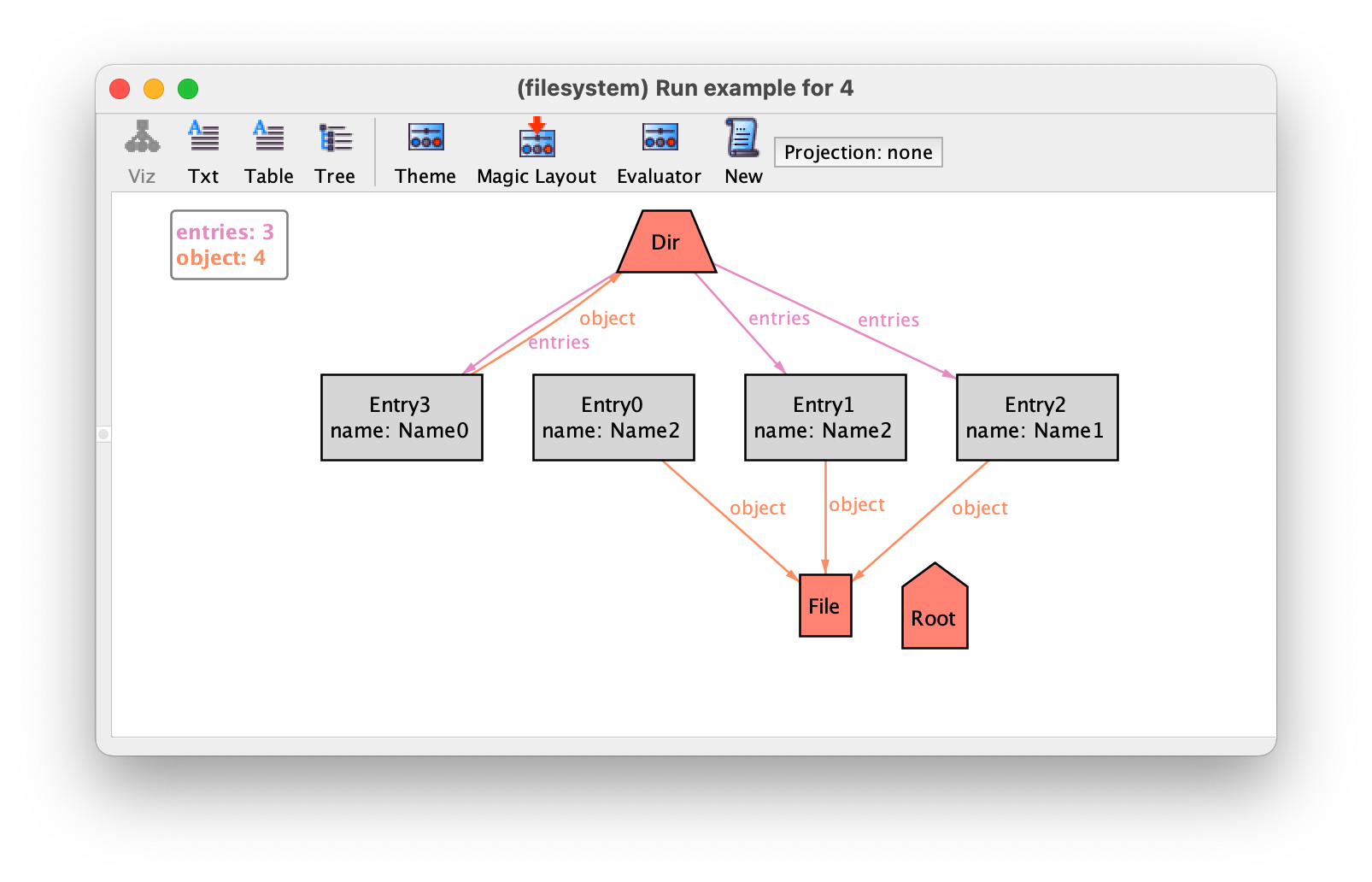
The problems identified above are now gone, but we still have two issues (the second already present in the previous instance):

• Entries not belonging to any directory.

• Directories contained in themselves.

To address the first issue we could just strengthen the first fact introduced above to demand that every entry belongs to one and exactly one directory.

fact {// Entries must belong to exactly one a directoryentries in Dir one -> Entry
}

Concerning the second issue, to forbid directories from containing themselves as entries, we can use the previously described expression d.entries.object to determine the objects contained in a directory d. Then we just need to forbid d itself from being a member of this set.

fact {// Directories cannot contain themselvesall d : Dir | d not in d.entries.object
}

Re-executing again command example and iterating a couple of times with New reveals no more issues. Obviously, it is impossible to manually inspect all possible instances, so we will proceed with the verification of our desired assertion, namely that the file system contains no partitions.

Assertion verification

To specify this assertion we need to determine the set of all objects that are reachable from the root. We have already seen how to determine the set of objects that are directly contained in a directory. Namely, Root.entries.object is the set of objects directly contained in the Root directory. The set of objects reachable from Root contains not only these, but also the objects that they contain, which can be determined as

Root.entries.object.entries.object

Of course, we also need to include the objects contained in these, and so on, and so on. Essentially, we would like to determine the following set:

Root.entries.object +
Root.entries.object.entries.object +
Root.entries.object.entries.object.entries.object +
...

The problem is how to fill in the ... in this expression: ultimately the number of times we need to compose entries.object depends on the size of our file system, and we would like our specification to be independent of this value. Fortunately, relational logic includes a so-called transitive closure operator (^) that when applied to a binary relation (or relational expression) determines the binary relation that results from taking the union of all its possible compositions. Essentially, given a relation r, ^r is the same as r + r.r + r.r.r + .... Seeing our instances as labelled graphs, the expression x.^r will determine the set of all atoms that can be reached from atom x by navigating in one or more steps via arrows labelled with r. Transitive closure is the reason why relational logic is strictly more expressive than first-order logic: our desired assertion could not be expressed in first-order logic alone.

By using transitive closure applied to relational expression entries.object we can determine the set of all objects reachable from root. To ensure that there are no partitions, this set must contain all objects (except the root itself). Our desired assertion can thus be specified as follows.

assert no_partitions {// Every object is reachable from the rootObject - Root = Root.^(entries.object)
}

To verify that this assertion is a consequence of all the facts that have been imposed before, we can define a check command.

check no_partitions

Unfortunately, executing this command reveals a counter-example.

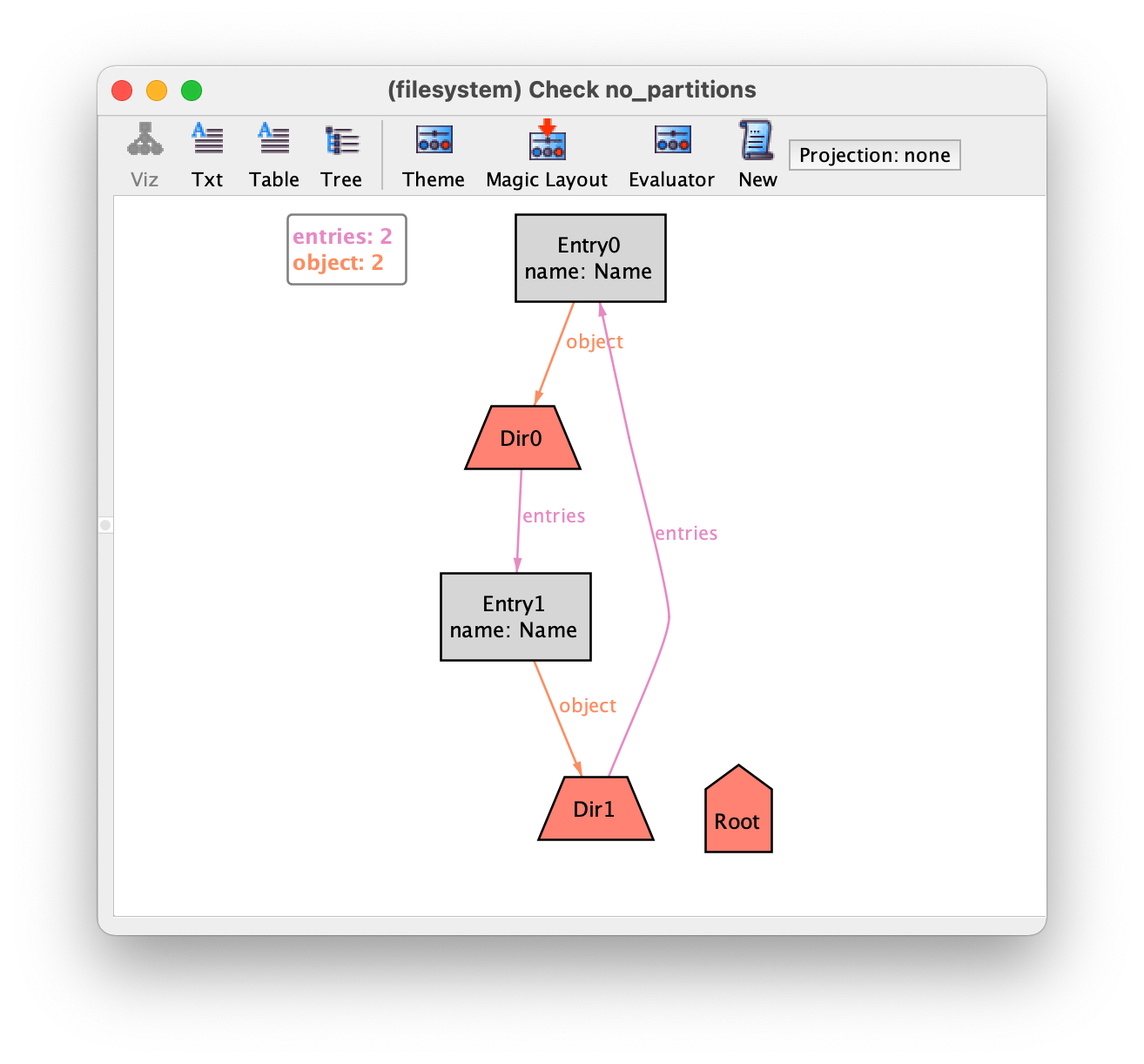
The problem is that we have two directories that contain each other. Fortunately, this counter-example is not an issue in real file systems, but exposes a problem in our specification. One of the facts specified above imposed that no directory can contain itself, but this alone is not sufficient: a directory cannot contain itself directly, nor indirectly. To fix that fact, we can again use the transitive closure operator to determine the set of all objects reachable from any directory d, and then disallow d from being a member of this set.

fact {// Directories cannot contain themselves directly or indirectlyall d : Dir | d not in d.^(entries.object)
}

Re-executing the check command no longer yields counter-examples. Although with the bounded analysis performed by the Analyzer we can never be entirely sure that the assertion is valid, we can set a higher scope to increase our confidence that that is indeed the case.

check no_partitions for 6

Tip

Be sure your specification is still consistent!

You should always be wary of the results of checking your assertions, in particular when they yield no counter-examples. Recall that a check command checks that an assertion is implied by the conjunction of all declared facts. If your facts are inconsistent, in the sense that their conjunction is false, or admit only very trivial instances (for example empty ones), your assertion can be trivially true. For example, in this example we changed one of the facts before our final check that yielded no counter-examples. We should have checked that this change did not accidentally made our specification inconsistent. To do so we could execute a run command after the final check, and iterate a bit through the returned instances to make sure the specification is still consistent and admits non-trivial file systems. Of course, just pressing New is not the ideal method to check if interesting file system examples are still possible. In chapter Alloy modelling tips we will see how to define run commands that behave like unit tests that directly search for specific instances of a specification.

So far we used only a reduced subset of all relational logic operators that are part of Alloy’s syntax. We did use the two most important ones, composition (.) and transitive closure (^), and with these alone (plus the standard set theory operators) it is possible to write most facts and assertions of interest. For a complete list of relational logic operators please see the A relational logic primer chapter.

Using higher-arity relations

abstract sig Object {}sig File extends Object {}sig Dir extends Object {contents : Name -> Object
}one sig Root extends Dir {}sig Name {}fact {// Different entries in the same directory must have different namesall d : Dir, n : Name | lone n.(d.contents)
}fact {// A directory cannot be contained in more than one directoryall o : Dir | lone contents.o
}fact {// Directories cannot contain themselves directly or indirectlyall d : Dir | d not in d.^{ d : Dir, o : Object | some d.contents.o }
}fact {// Every object except the root is contained somewhereName.(Object.contents) = Object - Root
}

 PreviousNext