VAE 理论推导及代码实现

文章列表

VAE 理论推导及代码实现

熵、交叉熵、KL 散度的概念

熵（Entropy)

假设 p (x）是一个分布函数，满足在 x 上的积分为 1，那么 $p (x)$ 的熵定义为 $H (p (x))$ ，这里我们简写为 $H (p)$
$H(p)=∫p(x)log⁡1p(x)dxH(p)=\\int p(x) \\log \\frac{1}{p(x)} dx$
直观上，越分散的分布函数熵越大。越集中的分布函数熵越小。熵的最小值为 0.

从信息论的角度来说，熵又叫信息熵，它的大小表示信息量的多少，分散的分布函数可能性多、拿到 p (x）后对于 x 的推断不确定性大，即信息量大，而对于 p © =1 这种情况拿到分布函数直接就拿到了结果，因此信息量为 0

交叉熵（Cross-Entropy)

假设 $p (x)$ 、 $q (x)$ 是两个分布函数，交叉熵的小大评价了这两个分布函数的相似与否。 $p$ 和 $q$ 的交叉熵记为 $H (p, q)$
$q)=\\int p(x) \\log \\frac{1}{q(x)} d x$

交叉熵小一分布相似；交叉熵大一分布不相似。交叉熵最大为无穷大，最小为 $p$ 的熵 $H (p)$

KL 散度

假设 $p (x)$ 、 $q (x)$ 是两个分布函数，KL 散度的小大评价了这两个分布函数的相似与否，同时考虑了 $K L (x)$ 这个分布的信息量。记为 $K L (p, q)$ 。注意： $K L (p, q)$ 也不一定等于 $K L (q, p)$ 。
$K L (p, q) = H (p, q) - H (p)$
$∫p(x)log⁡1q(x)dx−∫p(x)log⁡1p(x)dx=∫p(x)log⁡p(x)q(x)dx\\begin{aligned} & \\int p(x) \\log \\frac{1}{q(x)} d x-\\int p(x) \\log \\frac{1}{p(x)} d x \\\\ & =\\int p(x) \\log \\frac{p(x)}{q(x)} d x \\end{aligned}$

KL散度小—分布相似 & $[p (x)$ 分散 | $p (x)$ 信息量大]。
$KL\\mathrm{KL}$ 散度大–分布不相似 & $[p (x)$ 集中 $∣p(x)\\mid p(x)$ 信息量小]。
$KL\\mathrm{KL}$ 散度最小值为 $0 : p (x)$ 和 $q (x)$ 完全相同时。

概率知识

将p(x)其改写为包含了传入参数的形式
$p(x)=∑zp(x∣z)p(z)p(x)=\\sum_z p(x \\mid z) p(z)$

连续分布时，该式就变成了
$p(x)=∫z⁡p(x∣z)p(z)dzp(x)=\\int_z^{\\operatorname{}} p(x \\mid z) p(z) d z$

$p (z)$ 可以是任意分布，在VAE中我们常常假设p(z)服从标准正态分布。

变分方法

Intractability:
$pθ(z∣x)=pθ(x∣z)pθ(z)/pθ(x)pθ(x)=∫pθ(z)pθ(x˙∣z)dz\\begin{aligned} p_{\\boldsymbol{\\theta}}(\\mathbf{z} \\mid \\mathbf{x}) & =p_{\\boldsymbol{\\theta}}(\\mathbf{x} \\mid \\mathbf{z}) p_{\\boldsymbol{\\theta}}(\\mathbf{z}) / p_{\\boldsymbol{\\theta}}(\\mathbf{x}) \\\\ p_{\\boldsymbol{\\theta}}(\\mathbf{x}) & =\\int p_{\\boldsymbol{\\theta}}(\\mathbf{z}) p_{\\boldsymbol{\\theta}}(\\dot{\\mathbf{x}} \\mid \\mathbf{z}) d \\mathbf{z} \\end{aligned}$
$p(z∣x(i))=p(z,x(i))p(x(i))=p(x=x(i)∣z=z(i))p(z=z(i))∫z(i)p(x=x(i)∣z=z(i))p(z=z(i))dz(i)=p(x(i)∣z)p(z)∫zp(x(i)∣z)p(z)dz\\begin{aligned} p\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right) & =\\frac{p\\left(\\mathbf{z}, \\mathbf{x}^{(i)}\\right)}{p\\left(\\mathbf{x}^{(i)}\\right)} \\\\ & =\\frac{p\\left(\\mathbf{x}=\\mathbf{x}^{(i)} \\mid \\mathbf{z}=\\mathbf{z}^{(i)}\\right) p\\left(\\mathbf{z}=\\mathbf{z}^{(i)}\\right)}{\\int_{\\mathbf{z}^{(i)}} p\\left(\\mathbf{x}=\\mathbf{x}^{(i)} \\mid \\mathbf{z}=\\mathbf{z}^{(i)}\\right) p\\left(\\mathbf{z}=\\mathbf{z}^{(i)}\\right) d \\mathbf{z}^{(i)}} \\\\ & =\\frac{p\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right) p(\\mathbf{z})}{\\int_{\\mathbf{z}} p\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right) p(\\mathbf{z}) d \\mathbf{z}} \\end{aligned}$
参考：https://zhuanlan.zhihu.com/p/519448634

如果假设参数 $θ\\theta$ 已知, 那么先验分布 $pθ(z)p_\\theta(\\mathbf{z})$ 和条件似然函数 $pθ(x(i)∣z)p_\\theta\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right)$ 就都是已知的。理论上来说, 只要把分母里的积分项 $∫zpθ(x(i)∣z)p(z)dz\\int_{\\mathbf{z}} p_\\theta\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right) p(\\mathbf{z}) d \\mathbf{z}$ 计算出来, 那整个后验分布 $p(z∣x(i))p\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 就可以求了, 后验推断问题也就解决了。但是, 现实很骨感, 在没有对 $pθ(z)p_\\theta(\\mathbf{z})$ 和 $pθ(x(i)∣z)p_\\theta\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right)$ 作任何简化假设的前提下, 这个积分基本上是没有解析解的。你想硬着头皮解, 那么基本意味着你要穷举隐变量 $z\\mathbf{z}$ 的所有可能取值, 假设 $z\\mathbf{z}$ 有 $k$ 个维度, 每个维度采样 $n$ 个取值, 那么这个穷举过程的复杂度就是 $O(nk)O\\left(n^k\\right)$ 。

当然也有人用MCMC来做积分项的估计，虽然这个方案做采样估计很精准，但是费时费力，很难适用于大数据场景。所以一般更常见的方案是采用变分方法（variational method），它可以绕过对积分项的求解，通过把统计推断问题转化成参数优化问题来实现“降维打击”。

首先变分方法会设置一个新的参数化分布 $qϕ(z∣x(i))q_\\phi\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ , 它的参数是 $ϕ\\phi$ , 我们把它称作"识别模型" (原文记作recognition model) 。变分方法的核心思想是：直接让“识别模型”去拟合后验分布 $pθ(z∣x(i))p_\\theta\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ , 只要近似到位, 那么采用 $qϕ(z∣x(i))q_\\phi\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 作为后验推断的结果就行了。如何做近似呢? 很简单, 直接最小化 $qϕ(z∣x(i))q_\\phi\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 和 $pθ(z∣x(i))p_\\theta\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 两者间的KL散度即可。

就这样，变分方法把原来的统计推断问题转化成了优化问题：

Approximation $pθ(z∣x)≅qϕ(z∣x)\\quad p_\\theta(z \\mid x) \\cong q_\\phi(z \\mid x)$
$\\begin{aligned} & D_{K L}\\left(q_\\phi(z \\mid x) \\| p_\\theta(z \\mid x)\\right)=-\\sum_{\\text {decoder }} q_\\phi(z \\mid x) \\log \\left(\\frac{p_\\theta(z \\mid x)}{q_\\phi(z \\mid x)}\\right)=-\\sum_z q_\\phi(z \\mid x) \\log \\left(\\frac{\\frac{p_\\theta(x, z)}{p_\\theta(x)}}{q_\\phi(z \\mid x)}\\right) \\\\ & =-\\sum_z q_\\phi(z \\mid x)\\left[\\log \\left(\\frac{p_\\theta(x, z)}{q_\\phi(z \\mid x)}\\right)-\\underline{\\log \\left(p_\\theta(x)\\right)}\\right] \\\\ & \\begin{array}{c} \\text { non-negative } \\\\ \\log \\left(p_\\theta(x)\\right) \\end{array}=K L\\left(q_\\phi(z \\mid x) \\| p_\\theta(z \\mid x)\\right)+\\sum_z q_\\phi(z \\mid x) \\log \\left(\\frac{p_\\theta(x, z)}{q_\\phi(z \\mid x)}\\right) \\\\ & =D_{K L}\\left(q_\\phi(z \\mid x)|| p_\\theta(z \\mid x)\\right)+\\frac{L(\\theta, \\phi ; x)}{\\text { Variational lower bound }} \\\\ & \\end{aligned}$

Maximize the lower bound
$\\begin{aligned} & L(\\theta, \\phi ; x)=\\sum_z q_\\phi(z \\mid x) \\log \\left(\\frac{p_\\theta(x, z)}{q_\\phi(z \\mid x)}\\right)=\\sum_z q_\\phi(z \\mid x) \\log \\left(\\frac{p_\\theta(x \\mid z) p_\\theta(z)}{q_\\phi(z \\mid x)}\\right) \\\\ &= \\sum_z q_\\phi(z \\mid x)\\left[\\log \\left(p_\\theta(x \\mid z)\\right)+\\log \\left(\\frac{p_\\theta(z)}{q_\\phi(z \\mid x)}\\right)\\right] \\\\ &= \\frac{E_{q_\\phi(z \\mid x)}\\left[\\log \\left(p_\\theta(x \\mid z)\\right)\\right]}{\\text { Reconstruction Loss }}-\\frac{D_{K L}\\left(q_\\phi(z \\mid x) \\| p_\\theta(z)\\right)}{\\text { Regularization Loss }} \\end{aligned}$

$L(θ,ϕ;x)=∑zqϕ(z∣x)log⁡(pθ(x,z)qϕ(z∣x))=∑zqϕ(z∣x)log⁡(pθ(x∣z)pθ(z)qϕ(z∣x))=∑zqϕ(z∣x)[log⁡(pθ(x∣z))+log⁡(pθ(z)qϕ(z∣x))]\\begin{gathered} L(\\theta, \\phi ; x)=\\sum_z q_\\phi(z \\mid x) \\log \\left(\\frac{p_\\theta(x, z)}{q_\\phi(z \\mid x)}\\right)=\\sum_z q_\\phi(z \\mid x) \\log \\left(\\frac{p_\\theta(x \\mid z) p_\\theta(z)}{q_\\phi(z \\mid x)}\\right) \\\\ =\\sum_z q_\\phi(z \\mid x)\\left[\\log \\left(p_\\theta(x \\mid z)\\right)+\\log \\left(\\frac{p_\\theta(z)}{q_\\phi(z \\mid x)}\\right)\\right] \\end{gathered}$

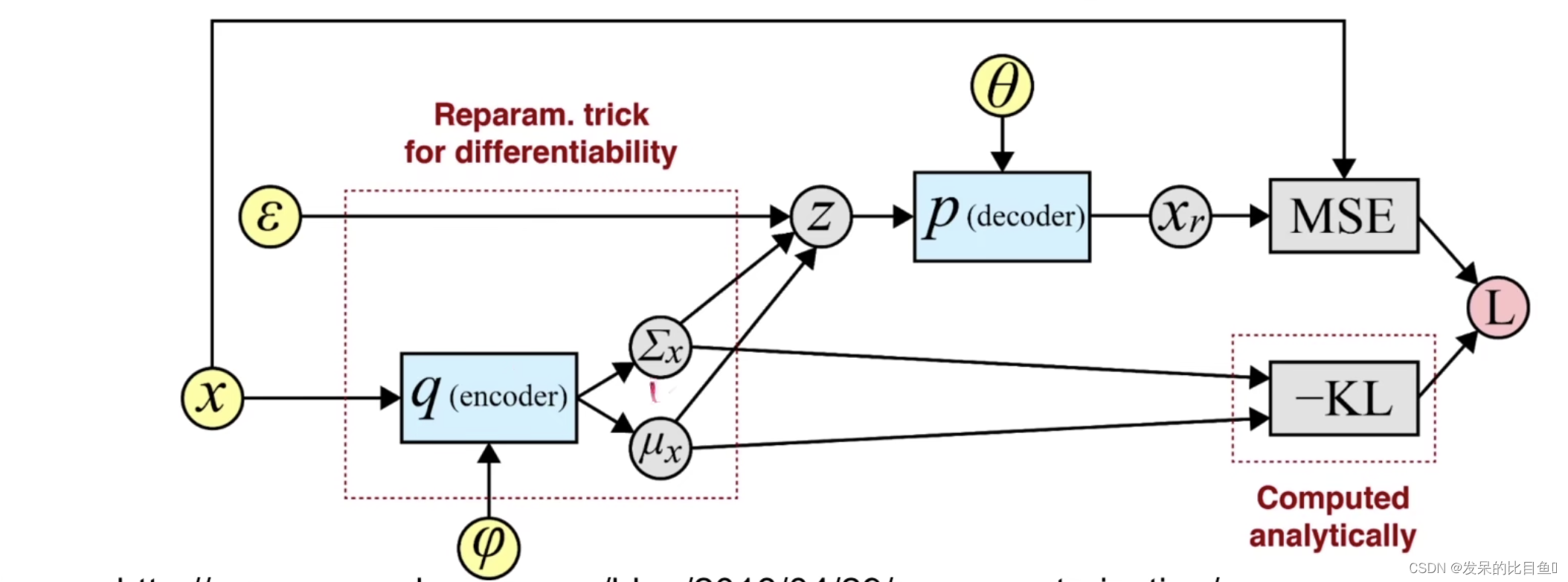
Regularization Loss（重参数化）

而在实践中, 一般不对 $qϕ(z∣x(i))q_\\phi\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 直接作采样, 采用 reparameterization trick 来简化操作, 我们设 $z(i,l)=gϕ(ϵ(i;l);x(i))\\mathbf{z}^{(i, l)}=g_\\phi\\left(\\epsilon^{(i ; l)} ; \\mathbf{x}^{(i)}\\right)$ , 其中 $gϕg_\\phi$ 是一个拟合函数 (e.g. 神经网络) , 而噪声 $ϵ(i;l)\\epsilon^{(i ; l)}$ 可以通过采样得到, 一般直接采样自简单的标准正态分布。

$∫qθ(z∣x)log⁡p(z)dz=∫N(z;μ,σ2)log⁡N(z;0,I)dz\\int q_\\theta(z \\mid x) \\log p(z) d z=\\int N\\left(z ; \\mu, \\sigma^2\\right) \\log N(z ; 0, I) dz$
$f(x)=1σ2πe−12(x−μσ)2f(x)=\\frac{1}{\\sigma \\sqrt{2 \\pi}} e^{-\\frac{1}{2}\\left(\\frac{x-\\mu}{\\sigma}\\right)^2}$

$z\\begin{aligned} & =\\int N\\left(z ; \\mu, \\sigma^2\\right)\\left(-\\frac{1}{2} z^2-\\frac{1}{2} \\log (2 \\pi)\\right) d z=-\\frac{1}{2} \\int N\\left(z ; \\mu, \\sigma^2\\right) z^2 d z-\\frac{J}{2} \\log (2 \\pi) \\\\ & =-\\frac{J}{2} \\log (2 \\pi)-\\frac{1}{2} E_{z \\sim N\\left(z ; \\mu, \\sigma^2\\right)}\\left[Z^2\\right] \\\\ & =-\\frac{J}{2} \\log (2 \\pi)-\\frac{1}{2}\\left(E_{z \\sim N\\left(z ; \\mu, \\sigma^2\\right)}[Z]^2+\\operatorname{Var}(Z)\\right) \\\\ & =-\\frac{J}{2} \\log (2 \\pi)-\\frac{1}{2} \\sum_{j=1}^J\\left(\\mu_j^2+\\sigma_j^2\\right) \\quad \\text { Let } J \\text { be the dimensionality of } z \\end{aligned}$

L1用于最小化 $K L (q (z ∣ x) ∣∣ p (z))$ ，VAE假设 $q (z ∣ x)$ 的分布为正态分布，而 $p (z)$ 为标准正态分布。计算两个正态分布之间的KL散度的公式如下：
$L\\left(N\\left(\\mu_1, \\sigma_1^2\\right), N\\left(\\mu_2, \\sigma_2^2\\right)\\right)=\\log \\frac{\\sigma_2}{\\sigma_1}+\\frac{\\sigma_1^2+\\left(\\mu_1-\\mu_2\\right)^2}{2 \\sigma_2^2}-\\frac{1}{2}$

由于此处p(z)为标准正态分布，因此其μ为0，σ为1，那么我们带入后可得
$L1=−12(log⁡σ2−σ2−μ2+1)L_1=-\\frac{1}{2}\\left(\\log \\sigma^2-\\sigma^2-\\mu^2+1\\right)$

采用reparameterization trick有两大好处：

由于分布 $qϕ(z∣x(i))q_\\phi\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 可能是一个比较复杂的函数, 直接采样操作费时费力, 而且采样方差可能很大, 不利于收玫, 通过reparameterization可以简化操作, 提高效率, 提高数值上的稳定性;
假设我们不考虑采样难度, 直接对 $qϕ(z∣x(i))q_\\phi\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)$ 采样, 那么梯度反向传播的时候, 损失函数中的 $1L∑l=1L[log⁡pθ(x(i)∣z(i,l))]\\frac{1}{L} \\sum_{l=1}^L\\left[\\log p_\\theta\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}^{(i, l)}\\right)\\right]$ 是没法对 $ϕ\\phi$ 求导的, 这样损失函数 $L(ϕ,θ,x(i))\\mathcal{L}\\left(\\phi, \\theta, \\mathbf{x}^{(\\mathbf{i})}\\right)$ 只能通过KL散度的梯度对 $ϕ\\phi$ 做优化, 这和我们做联合参数优化的意图是违背的。所以使用reparameterization trick 让 $z(i,l)=gϕ(ϵ(i;l);x(i))\\mathbf{z}^{(i, l)}=g_\\phi\\left(\\epsilon^{(i ; l)} ; \\mathbf{x}^{(i)}\\right)$ , 实际上是让参数 $θ,ϕ\\theta, \\phi$ 可以同时得到期望项和KL散度项的反传梯度进行优化, 让模型学得更好。

Reconstruction Loss

$L(θ,ϕ;x(i))=−DKL(qϕ(z∣x(i))∥pθ(z))‾+Eqϕ(z∣x(i))[log⁡pθ(x(i)∣z)]‾−DKL((qϕ(z)∥pθ(z))=∫qθ(z)(log⁡pθ(z)−log⁡qθ(z))dz=12∑j=1J(1+log⁡((σj)2)−(μj)2−(σj)2)f∗=arg⁡max⁡f∈FEz∼qx∗(log⁡p(x∣z))=arg⁡max⁡f∈FEz∼qx∗(−∥x−f(z)∥22c)\\begin{aligned} & \\mathcal{L}\\left(\\boldsymbol{\\theta}, \\boldsymbol{\\phi} ; \\mathbf{x}^{(i)}\\right)=\\underline{-D_{K L}\\left(q_{\\boldsymbol{\\phi}}\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right) \\| p_{\\boldsymbol{\\theta}}(\\mathbf{z})\\right)}+\\underline{\\mathbb{E}_{q_{\\boldsymbol{\\phi}}\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)}\\left[\\log p_{\\boldsymbol{\\theta}}\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right)\\right]} \\\\ & -D_{K L}\\left(\\left(q_{\\boldsymbol{\\phi}}(\\mathbf{z}) \\| p_{\\boldsymbol{\\theta}}(\\mathbf{z})\\right)=\\int q_{\\boldsymbol{\\theta}}(\\mathbf{z})\\left(\\log p_{\\boldsymbol{\\theta}}(\\mathbf{z})-\\log q_{\\boldsymbol{\\theta}}(\\mathbf{z})\\right) d \\mathbf{z}\\right. \\\\ & =\\frac{1}{2} \\sum_{j=1}^J\\left(1+\\log \\left(\\left(\\sigma_j\\right)^2\\right)-\\left(\\mu_j\\right)^2-\\left(\\sigma_j\\right)^2\\right) \\\\ & f^*=\\underset{f \\in F}{\\arg \\max } \\mathbb{E}_{z \\sim q_x^*}(\\log p(x \\mid z)) \\\\ & =\\underset{f \\in F}{\\arg \\max } \\mathbb{E}_{z \\sim q_x^*}\\left(-\\frac{\\|x-f(z)\\|^2}{2 c}\\right) \\\\ & \\end{aligned}$

$L(θ,ϕ;x(i))=−DKL(qϕ(z∣x(i))∥pθ(z))+Eqϕ(z∣x(i))[log⁡pθ(x(i)∣z)]\\mathcal{L}\\left(\\boldsymbol{\\theta}, \\boldsymbol{\\phi} ; \\mathbf{x}^{(i)}\\right)=-D_{K L}\\left(q_{\\boldsymbol{\\phi}}\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right) \\| p_{\\boldsymbol{\\theta}}(\\mathbf{z})\\right)+\\mathbb{E}_{q_{\\boldsymbol{\\phi}}\\left(\\mathbf{z} \\mid \\mathbf{x}^{(i)}\\right)}\\left[\\log p_{\\boldsymbol{\\theta}}\\left(\\mathbf{x}^{(i)} \\mid \\mathbf{z}\\right)\\right]$
VAE 理论推导及代码实现


import argparse
import torch
import torch.utils.data
from torch import nn, optim
from torch.nn import functional as F
from torchvision import datasets, transforms
from torchvision.utils import save_imageparser = argparse.ArgumentParser(description='VAE MNIST Example with Different Losses')
parser.add_argument('--batch-size', type=int, default=128, metavar='N',help='input batch size for training (default: 128)')
parser.add_argument('--epochs', type=int, default=100, metavar='N',help='number of epochs to train (default: 100)')
parser.add_argument('--no-cuda', action='store_true', default=False,help='enables CUDA training')
parser.add_argument('--seed', type=int, default=1, metavar='S',help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=100000, metavar='N',help='how many batches to wait before logging training status')
args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()torch.manual_seed(args.seed)device = torch.device("cuda" if args.cuda else "cpu")kwargs = {'num_workers': 1, 'pin_memory': True} if args.cuda else {}
train_loader = torch.utils.data.DataLoader(datasets.MNIST('./datasets', train=True, download=True,transform=transforms.ToTensor()),batch_size=args.batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(datasets.MNIST('./datasets', train=False, transform=transforms.ToTensor()),batch_size=args.batch_size, shuffle=True, **kwargs)class VAE(nn.Module):def __init__(self):super(VAE, self).__init__()self.fc1 = nn.Linear(784, 400)self.fc21 = nn.Linear(400, 20)self.fc22 = nn.Linear(400, 20)self.fc3 = nn.Linear(20, 400)self.fc4 = nn.Linear(400, 784)def encode(self, x):h1 = F.relu(self.fc1(x))return self.fc21(h1), self.fc22(h1)def reparameterize(self, mu, logvar):std = torch.exp(0.5*logvar)eps = torch.randn_like(std)return mu + eps*stddef decode(self, z):h3 = F.relu(self.fc3(z))return torch.sigmoid(self.fc4(h3))def forward(self, x):mu, logvar = self.encode(x.view(-1, 784))z = self.reparameterize(mu, logvar)return self.decode(z), mu, logvarmodel = VAE().to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)### 1.
# Reconstruction + KL divergence losses summed over all elements and batch
def loss_function_original(recon_x, x, mu, logvar):BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')# 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())return BCE + KLD### 2. 
# using the loss function which only consider reconstruction term.
def loss_function_only_recon(recon_x, x):BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')return BCE### 3. 
# be careful of the way two losses calculated.
# the only difference of this loss function is that the second term - KLD
# is "mean".
def loss_function_o1(recon_x, x, mu, logvar):BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='sum')KLD = -0.5 * torch.mean(1 + logvar - mu.pow(2) - logvar.exp())return BCE + KLD### 4.
def loss_function_o2(recon_x, x, mu, logvar):BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction='mean')KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())return BCE + KLD### 5.
def loss_function_kld(recon_x, x, mu, logvar):KLD = -0.5 * torch.mean(1 + logvar - mu.pow(2) - logvar.exp())return KLD### 6.
# apply the l1 loss
def loss_function_l1(recon_x, x, mu, logvar):L1 = F.l1_loss(recon_x, x.view(-1, 784), reduction='sum')KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())return L1 + KLD### 7.
# apply the MSE loss
def loss_function_l2(recon_x, x, mu, logvar):L1 = F.mse_loss(recon_x, x.view(-1, 784), reduction='sum')KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())return L1 + KLDdef train(epoch):model.train()train_loss = 0for batch_idx, (data, _) in enumerate(train_loader):data = data.to(device)optimizer.zero_grad()recon_batch, mu, logvar = model(data)which_loss = 7if which_loss==1:loss = loss_function_original(recon_batch, data, mu, logvar)elif which_loss==2:loss = loss_function_only_recon(recon_batch, data)elif which_loss==3:loss = loss_function_o1(recon_batch, data, mu, logvar)elif which_loss==4:loss = loss_function_o2(recon_batch, data, mu, logvar)elif which_loss==5:loss = loss_function_kld(recon_batch, data, mu, logvar)elif which_loss==6:loss = loss_function_l1(recon_batch, data, mu, logvar)elif which_loss==7:loss = loss_function_l2(recon_batch, data, mu, logvar)loss.backward()train_loss += loss.item()optimizer.step()print('====> Epoch: {} Average loss: {:.4f}'.format(epoch, train_loss / len(train_loader.dataset)))def test(epoch):model.eval()with torch.no_grad():for i, (data, _) in enumerate(test_loader):data = data.to(device)recon_batch, mu, logvar = model(data)if (i == 0) and (epoch % 10 == 0):n = min(data.size(0), 8)comparison = torch.cat([data[:n],recon_batch.view(args.batch_size, 1, 28, 28)[:n]])save_image(comparison.cpu(),'vae_img/7_m_reconstruction_' + str(epoch) + '.png', nrow=n)if __name__ == "__main__":for epoch in range(1, args.epochs + 1):train(epoch)test(epoch)if epoch%10 == 0:with torch.no_grad():sample = torch.randn(64, 20).to(device)sample = model.decode(sample).cpu()save_image(sample.view(64, 1, 28, 28),'vae_img/7_m_sample_' + str(epoch) + '.png')

参考

https://zhuanlan.zhihu.com/p/345360992

VAE 理论推导及代码实现

VAE 理论推导及代码实现

熵、交叉熵、KL 散度的概念

熵（Entropy)

交叉熵（Cross-Entropy)

KL 散度

概率知识

变分方法

Regularization Loss（ 重参数化）

Reconstruction Loss

参考

相关问题

公告

Regularization Loss（重参数化）