LeetCode-45. 跳跃游戏 II

题目来源
-
- 贪心
- 动态规划
- 动态规划+贪心
题目来源
45. 跳跃游戏 II
贪心
如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置)
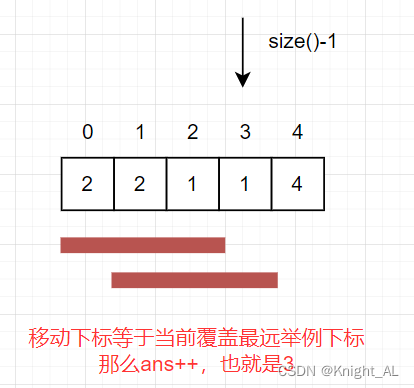
如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。
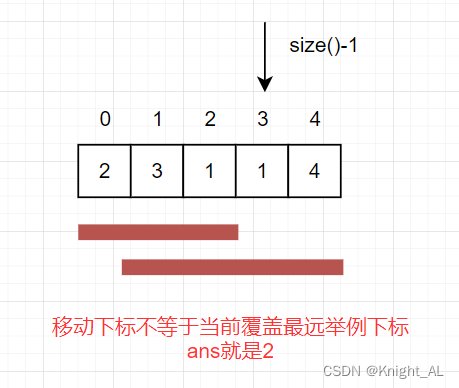
class Solution {public int jump(int[] nums) {int ans = 0;int cur = 0;int next = 0;for(int i = 0;i<nums.length-1;i++){next = Math.max(next,i+nums[i]);if(i == cur){cur = next;ans++;}}return ans;}
}

动态规划
- 1.确定dp数组以及下标的含义
定义状态 dp[i] 表示为:跳到下标 i 所需要的最小跳跃次数。
- 2.确定递推公式
对于当前位置 i,如果之前的位置 j 能够跳到位置 i 需要满足:位置 j加上位置 j 所能跳到的最远长度要大于等于 i,即 j + nums[j] >= i 。
而跳到下标 i 所需要的最小跳跃次数则等于满足上述要求的位置 j 中最小跳跃次数加 1,即 dp[i] = Math.min(dp[i], dp[j] + 1)。
- 3.dp数组如何初始化
初始状态下,跳到下标 0 需要的最小跳跃次数为 0,即 dp[0] = 0。
后面的初始化为最大值,因为我们要求最小值
for(int i = 1;i<dp.length;i++){dp[i] = Integer.MAX_VALUE;}
- 4.确定遍历顺序
从递归公式dp[i] = Math.min(dp[i], dp[j] + 1)中可以看出,遍历的顺序一定是从前到后遍历的
- 5.举例推导dp数组
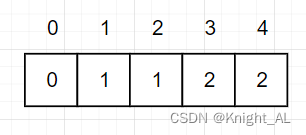
代码实现
class Solution {public int jump(int[] nums) {int[] dp = new int[nums.length];for(int i = 1;i<dp.length;i++){dp[i] = Integer.MAX_VALUE;}for(int i = 1;i<dp.length;i++){for(int j = 0;j<i;j++){if(j+nums[j]>=i){dp[i] = Math.min(dp[i],dp[j]+1);}}}return dp[dp.length-1];}
}

动态规划+贪心
有点贪心的含义,因为题目给了总是可以到达数组的最后一个位置
class Solution {public int jump(int[] nums) {if(nums.length == 1){return 0;}int[] dp = new int[nums.length];for(int i = 1;i<dp.length;i++){dp[i] = Integer.MAX_VALUE;}for(int i = 0;i<dp.length;i++){for(int j=i+1;j<=i+nums[i];j++){if(j>=dp.length-1){return dp[i]+1;}dp[j] = Math.min(dp[j],dp[i]+1);}}return dp[dp.length-1];}
}



