题目背景

众所周知，神J（Joker）每隔几天就会去成都法中假装上课，实际上是去玩指针。神J可以趁别人不注意掏出指针把自己指到任何位置（生物标本柜里大变活人？），或者把两个人的指针交换一下（成都法中版《你的名字》？），或者对着OJ念系统命令使得OJ随机变慢（mcfx：怎么这CPU睿频后反而变慢了）。

神树大人很不满意，因为树必须站在原地，而且神树大人也不会指针。但是神树大人是神，于是他打算把这个宇宙的数据库删了跑路，这样无所事事的神J就只能和神树大人玩牌了。

题目描述

现在有个长为$T$的字符串$S$和$n$个小字符串aia_iai​。

给定一个长为$m$的数组$R$，数组下标从1开始，初始有一个空字符串$X$，神树大人打算进行$Q$次操作，第$i$次操作会把小字符串aR(i−1)modm+1a_{R_{(i-1)\\bmod m+1}}aR(i−1)modm+1​​丢到这个$X$的末尾。

每次操作后，神树大人会检查这个字符串$X$是否存在一个后缀使得任意排列后可以变成$S$。

问有多少次这个字符串$X$存在一个后缀使得任意排列后可以变成$S$（即所有字符出现次数相同）。

可惜的是，这个字符串字符大小高达10510^5105，所以你必须读入一个整数数组

输入格式

输入$n,T,Q$

接下来输入$T$个数表示字符串$S$

接下来输入$n$行，每行第一个数$len$表示长度，接下来输入$len$个数表示这个小字符串，输入的每个数都在[0,105][0,10^5][0,105]范围内。

接下来输入$m$

输入一行$m$个数，表示$R$。

输出格式

输出答案

样例 #1

样例输入 #1

5 5 20
2 2 0 2 0
2 2 0
2 0 2
3 0 2 0
3 0 2 0
2 2 2
10
2 1 5 5 2 2 4 2 5 3

样例输出 #1

6

样例 #2

样例输入 #2

10 10 10000
0 1 1 1 0 1 1 0 0 0 
6 0 0 1 1 1 0 
6 0 0 0 0 0 0 
5 0 0 0 0 0 
4 1 0 0 0 
5 1 1 1 0 1 
2 1 1 
6 0 0 0 0 0 1 
1 0 
4 0 0 1 1 
1 1 
30
10 4 3 9 10 9 4 8 5 10 9 8 6 10 10 4 9 2 2 9 6 4 1 10 10 1 9 10 3 5

样例输出 #2

3001

提示

样例1解释：

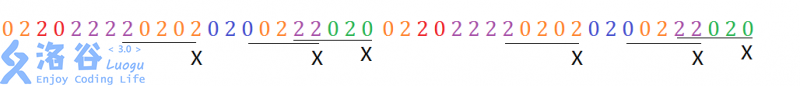
数据范围

对于所有数据，n,T,m≤105,1≤Ri≤n,Q≤109n,T,m\\leq 10^5,1\\leq R_i\\leq n,Q\\leq 10^9n,T,m≤105,1≤Ri​≤n,Q≤109，所有小字符串的总长不超过10510^5105，所有字符∈[0,105]\\in[0,10^5]∈[0,105]。

哈希、队列、模拟 - AC

判断两个字符串中各字符出现字数是否相等，如果用数组计数，一个一个比对，一定会超时。所以用哈希。
设字符$i$的出现次数是$cnt(i)$，则哈希值hsh=∑cnt(i)×BimodMODhsh=\\sum{cnt(i)\\times B^i} \\ mod\\ MODhsh=∑cnt(i)×Bi mod MOD, 其中B和MOD取两个质数。这里选择自然溢出。
每当一个小字符串被加进来，取后T位，判断哈希值是否与S相等即可。

但这样会超时，因为Q≤109Q\\leq 10^9Q≤109. 显然要找到循环。
第一反应是，每个R，即每m个小字符串为一个循环节。但这值得怀疑。如果一个循环节的长度不是T的倍数，会不会迫使循环节增长？这里我卡了很久。
事实上，这只是我的主观臆断。本题并不是把拼接的字符串每T个为一组划分，而是有一个长度为T的窗口随着字符串的拼接而移动。这会形成循环，因为每个循环节开始时，窗口左端的位置都一样，里面的内容都是上一个循环节的末尾。

前提是，字符串X中有至少T个字符。所以预处理出来。

窗口的移动，即后来的字符把先来的挤出去，用队列实现哈希值的转移。加上新的小字符串的哈希值，减去被挤出去的哈希值。被挤出去的常不是整个小字符串，而是其子串。常规地，对每个小字符串预处理前缀哈希值。
一个循环节的长度可能过长，这一问题被同时解决。
关于前T个字符，没有“被挤出来”的。可以初始化X为一个长度为T的空字符串。

凑不出整数个循环等问题，不再赘述。

回头来看，本题很简单，但我分析用了1h，打代码用了1h，主要卡在循环（本题中是自然且必然的，我却怀疑）、队列（没重点思考核心的“拼接字符串”操作，所以没能快速想到用队列进行模拟）。

const ull B = 122777;int n, t, q, m, len[MAXN], l, r[MAXM], ans, cnt;
ull s, pw[MAXT], res;
vector<ull> hsh[MAXN];int qa, qb, qc, p;
queue<int> que;void work(int j, int &ans) {int u = r[j];res += hsh[u][len[u]];que.push(u);int tmp = len[u];while (tmp) {int v = que.front();if (p + tmp < len[v]) {res -= hsh[v][p + tmp] - hsh[v][p];p += tmp;break;}res -= hsh[v][len[v]] - hsh[v][p];tmp -= len[v] - p;que.pop();p = 0;}if (res == s) ++ans;
}int main() {pw[0] = 1;for (int i = 1; i < MAXT; ++i) {pw[i] = pw[i - 1] * B;}scanf("%d%d%d", &n, &t, &q);for (int i = 1; i <= t; ++i) {int tmp; scanf("%d", &tmp);s += pw[tmp];}for (int i = 1; i <= n; ++i) {scanf("%d", len + i);hsh[i].push_back(0);for (int j = 1; j <= len[i]; ++j) {int tmp; scanf("%d", &tmp);hsh[i].push_back(hsh[i].back() + pw[tmp]);}}len[0] = t;hsh[0].push_back(0);for (int i = 1; i <= len[0]; ++i) {hsh[0].push_back(0);}scanf("%d", &m);for (int i = 1; i <= m; ++i) {scanf("%d", r + i);l += len[r[i]];} //cout << l << "\\n";qa = q / m; qb = q % m;qc = (t + l - 1) / l;p = 0; que.push(0);if (qc * m <= q) {for (int i = 1; i <= qc; ++i) {for (int j = 1; j <= m; ++j) {work(j, ans);}}}if (qa > qc) {for (int j = 1; j <= m; ++j) {work(j, cnt);}ans += cnt * (qa - qc);}for (int j = 1; j <= qb; ++j) {work(j, ans);}printf("%d\\n", ans);return 0;
}