风声雨声读书声，声声入耳不断行。
不成双，不成对，唯有自己最为重。
勤学苦练功力深，百年修得同舟心。

引言

还记得我们在IDA*算法中提到的那位探险家吗（IDA*算法传送门）？这次他历经千辛万苦，终于找到了一个充满宝藏的遗迹。这个遗址呈倒三角形，上面的房间中有通往下面房间的入口，但同一层的房间之间没有通道，如图所示。

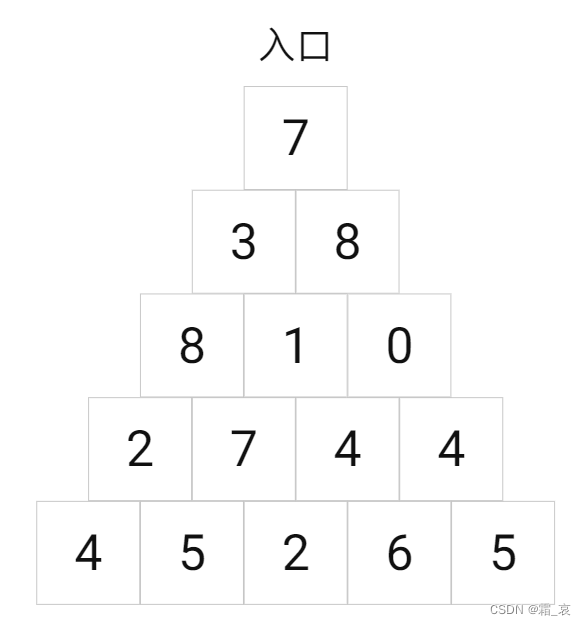
在进入遗迹之前，这位探险家已经得到了每个房间中有多少宝藏的准确情报，如图中数字所示。
这位探险家在进入一个房间之后，这个房间的入口会关闭，即他不能走回头路。在这种情况下，他应该如何走才能拿到最多的宝藏呢？

正文

分析

因为这次已经有了这个遗迹的所有情报，这位探险家当然可以模拟着把所有能走的路径都走一遍，这样就可以找到宝藏最多的那条路，这就是我们之前介绍的搜索思想。但不用想都知道，这种方法实在太累了！等你模拟完，别人都把宝藏抢走了。有没有什么巧妙的方法呢？
我们逐层考虑这个过程的逆过程：

1. 当我们从最后一层出来时，我们身上的宝藏数怎么计算？倒数第二层的宝藏数+最后一层房间内的宝藏数。
2. 那倒数第二层时身上的宝藏数怎么计算？倒数第三层的宝藏数+第二层房间内的宝藏数。

以此类推，一直到第二层时身上的宝藏数=第一层的宝藏数+第二层房间内的宝藏数，而到这里时所有数都是已知的。
到这里，我们只需要把这个过程再正推回去，一条路径就出现了。

图示

1. 探险家进入了第一层，得到了7个宝藏。
2. 进入第二层。如果进入左边，会得到10份宝藏；右边会得到15份宝藏。
   
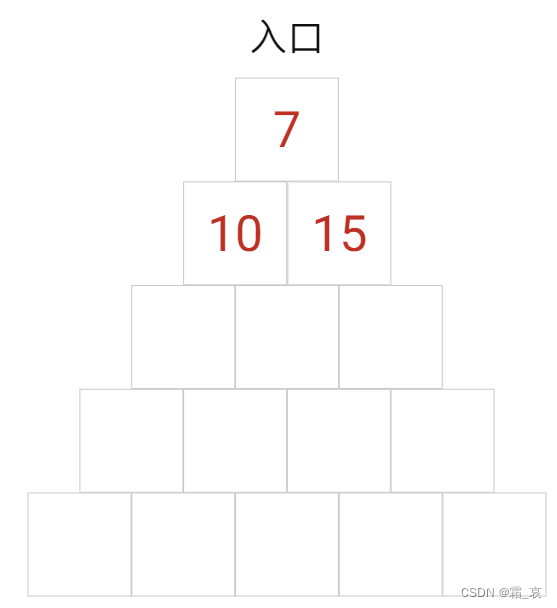
3. 进入第三层，注意中间的房间，从左边或右边都能进入这个房间，这里我们要记录的是当进入这个房间时能获得的最大宝藏数，因此我们假设他从右边进入房间能获得更多的16份宝藏。
   
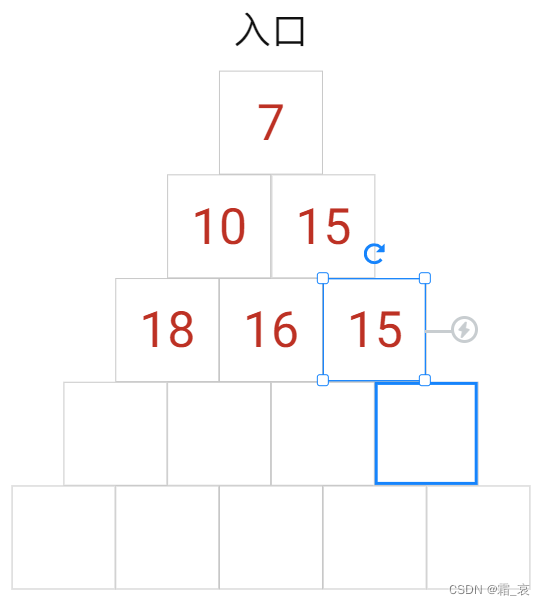
4. 重复上面的过程，完成第四层和第五层的模拟。
   
   
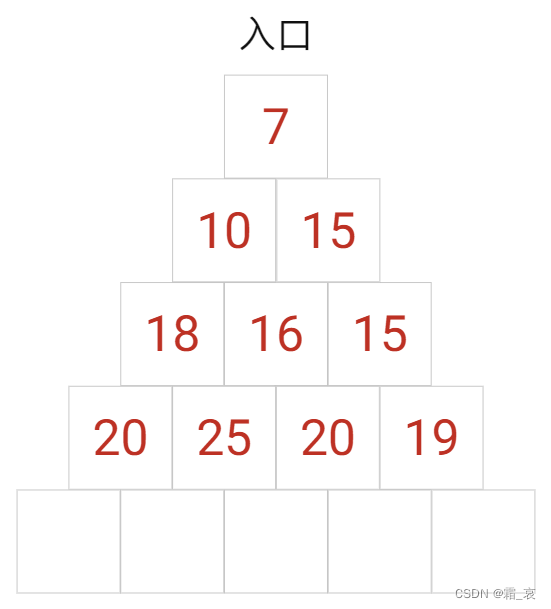
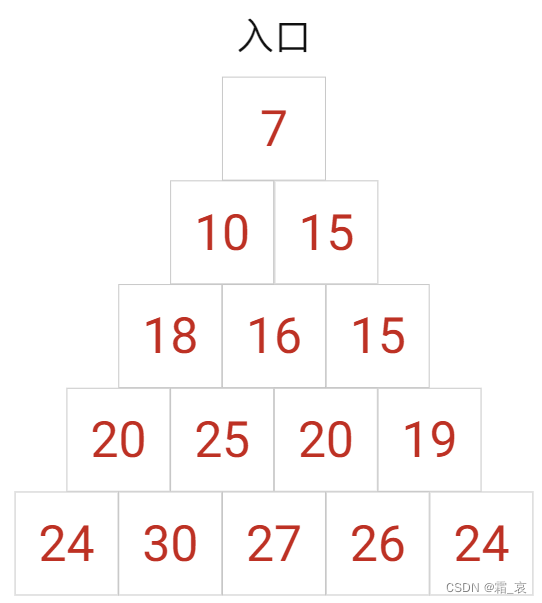
5. 接下来，我们从结果入手，可以很容易的看到，从第二个房间中出来时可以拿30份宝藏，是最多的。为了拿到这30份宝藏，我们需要找到我们从哪个房间进入的第五层；找到这个房间后，我们在寻找这个房间之前的房间…最后可以找出这样一条路径，算法结束。
   
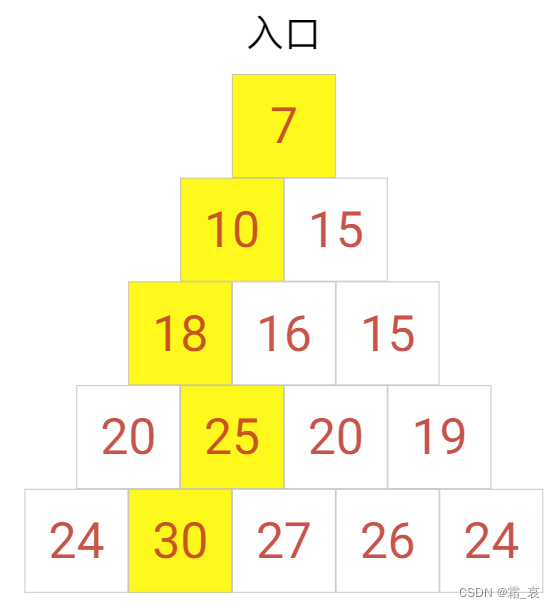
   明白了整个过程之后，或许你可以尝试自己写出代码。当然，你也可以直接看下面的代码：

代码

这是包含初始化，算法运行，输出结果的三个函数的代码，其中dp是算法运行的函数，fa是用于寻找一个房间的前一个房间的函数，我们在寻找路径时，只需要逐层找到所经过房间的上一个房间就可以了。

#define _CRT_SECURE_NO_WARNINGS 1
#include<algorithm>
#include<iostream>
using namespace std;
typedef struct node {int v;int fa_i;int fa_j;
};
node** room;
int n;
void ini()
{scanf("%d", &n);room = (node**)malloc(sizeof(node*) * (n+1));for (int i = 0; i <= n; i++) {room[i] = (node*)malloc(sizeof(node) * (n+1));}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {room[i][j].v = -1;room[i][j].fa_i = -1;room[i][j].fa_j = -1;}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {scanf("%d", &room[i][j].v);}}
}
void fa(int i,int j)//核心函数
{if (room[i-1][j].v==-1) {room[i][j].fa_i = i - 1;room[i][j].fa_j = j - 1;}else if (room[i-1][j - 1].v == -1) {room[i][j].fa_i = i - 1;room[i][j].fa_j = j;}else {if (room[i - 1][j].v > room[i-1][j - 1].v) {room[i][j].fa_i = i - 1;room[i][j].fa_j = j;}else {room[i][j].fa_i = i - 1;room[i][j].fa_j = j - 1;}}
}
void dp()
{for (int i = 2; i <= n; i++) {for (int j = 1; j <= i; j++) {if (room[i - 1][j].v == -1) {room[i][j].v += room[i - 1][j - 1].v;}else if (room[i-1][j - 1].v == -1) {room[i][j].v += room[i - 1][j].v;}else {room[i][j].v += max(room[i - 1][j].v, room[i - 1][j - 1].v);//转移方程}fa(i, j);}}
}
void print()
{int result=room[n][1].v;for (int i = 2; i <= n; i++) {if (room[n][i].v > result) {result = room[n][i].v;}}for (int i = 1; i <= n; i++) {if (room[n][i].v == result) {printf("\\n%d是结果\\n", result);int j=n, k=i;printf("(%d,%d) ", j, k);while (1) {int a = j;j = room[j][k].fa_i;k = room[a][k].fa_j;printf("(%d,%d) ", j, k);if (j == 1)break;}break;}}
}
int main(void)
{ini();dp();print();return 0;
}

总结

可以用动态规划解决的问题一般有几个共同点，我们用上面的题目来剖析一下：

1. 最优子结构：一个大问题的最优解包含其子问题的最优解，具体体现在转移方程：

room[i][j].v += max(room[i - 1][j].v, room[i - 1][j - 1].v);

在转移方程中，我们找room[i][j].v的最优解，是通过找到其多个子问题中的最大值；而子问题找到最优解的方法也是通过找它的多个子问题的最大值。在每个子结构中我们都找到的是它的子问题的最大值来实现子结构的最优解，这就是最优子结构。
2. 无后效性：这个很好理解，毕竟你每一步的解都是从上一步得出来的，不可能再回过头去改前面的值吧？
3. 重叠子问题：我觉得这个叫“重叠问题”更合适一些。再看转移方程：

room[i][j].v += max(room[i - 1][j].v, room[i - 1][j - 1].v);

我们通过比较两个值的最大值来得出一个问题的解。比较的前提是这两个值都和这个解有关系，有多种方式来得出这个问题的可能解（不是最优解），这就是重叠子问题。

再推荐一道比较经典且基础的动态规划问题：最长不下降子序列问题
题目:

给定一个长度为n的序列 A（n<=5000），求出一个最长的 A 的子序列，满足该子序列的后一个元素不小于前一个元素。

如果有需要的话，可以在评论区留言，我会专门写一篇这道题的题解。

————————————————————分割线——————————————————

说一些题外话。
搜索专栏的经典算法还剩下舞蹈链和α-β剪枝两种，鉴于这两种算法难度较大，笔者发起一个投票，大家可以按照自己的意愿投票。如果想看舞蹈链的人数较少，就暂时跳过这一部分，先介绍动态规划部分的算法。

动态规划基础到这里就结束啦，我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的算法讲解！