算法第十六期——动态规划(DP)之线性DP

【概述】
线性动态规划,是较常见的一类动态规划问题,其是在线性结构上进行状态转移,这类问题不像背包问题、区间DP等有固定的模板。
线性动态规划的目标函数为特定变量的线性函数,约束是这些变量的线性不等式或等式,目的是求目标函数的最大值或最小值。
因此,除了少量问题(如:LIS、LCS、LCIS等)有固定的模板外,大部分都要根据实际问题来推导得出答案。
【例题】最长公共子序列(LCS)
lanqiao0J题号1054
lanqiao0J题号1189
LCS 问题(Longest Common Subsequence),给定一个长度为n数组A和一个长度为m的数组B,求序列的最长公共子序列。
题目描述
输入描述
第一行为第一个字符序列,都是大写字母组成,以 . 结束,长度小于 5000。
第二行为第二个字符序列,都是大写字母组成,以 . 结束,长度小于 5000。
输出描述
第一行输出上述两个最长公共子序列的长度。
第二行输出所有可能出现的最长公共子序列个数,答案可能很大,只要将答案对
求余即可。
输入输出样例
输入
ABCBDAB. BACBBD.输出
4 7
题目大意:
一个给定序列的子序列,是在该序列中(不一定连续)删去若干元素后得到的序列。例如:X = {A,B,C,B, D,A, B},它的子序列有{A, B,C,B,A}、{A,B,D}、{B, C,D,B}等。给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列,最长公共子序列是长度最长的子序列。求两个最长公共子序列的长度和所有可能出现的最长公共子序列个数。
法一:暴力法
先找出A的所有子序列,然后 一 一 验证是否为Y的子序列。
如果A有m个元素,那么A有个子序列(集合的子集的个数),B有n个元素,总复杂度大于
法二:动态规划
dp[i][j]:序列Ai ()和Bj (b1~bj)的最长公共子序列的长度:dp[n][m]
分解为2种情况:
(1)当(当前两个子序列的最后一个相同)时,已求得
和
的最长公共子序列,在其尾部加上
或
即可得到
的最长公共子序列。状态转移方程:
dp[i]j]= dp[i-1][j-1]+1
(2)当时,求解两个子问题:
的最长公共子序列;
的最长公共子序列。取最大值,状态转移方程:
dp[i][j]=max{dp[i][j-1], dp[i-1][j]}
复杂度O(nm)
代码 :
使用交替滚动数组
(1)当时,状态转移方程:dp[i][i]= dp[i-1][j-1]+1
(2)当时,状态转移方程: dp[i][j]= max{dp[i][j-1], dp[i-1][j]}
n, m = map(int, input().split())
a = [0] + list(map(int, input().split())) # 从a[1]~a[n]
b = [0] + list(map(int, input().split())) # 从b[1]~b[n]
dp = [[0] * (m + 1) for _ in range(2)] # 注意这里是m,不是n
now = 0; old = 1
for i in range(1, n + 1):now, old = old, nowfor j in range(1, m + 1):if a[i] == b[j]:dp[now][j] = dp[old][j - 1] + 1 else: # ai≠bjdp[now][j] = max(dp[now][j - 1], dp[old][j]) print(dp[now][m])【例题】 最长递增子序列(LIS)
蓝桥骑士lanqi ao0J题号1188
题目描述
小明是蓝桥王国的骑士,他喜欢不断突破自我。这天蓝桥国王给他安排了 N 个对手,他们的战力值分别为 a1,a2,...,an,且按顺序阻挡在小明的前方。对于这些对手小明可以选择挑战,也可以选择避战。身为高傲的骑士,小明从不走回头路,且只愿意挑战战力值越来越高的对手。请你算算小明最多会挑战多少名对手。
输入描述
输入第一行包含一个整数 N,表示对手的个数。
第二行包含 N 个整数 a1,a2,...,an,分别表示对手的战力值。
。
输出描述
输出一行整数表示答案。
输入输出样例
输入
6 1 4 2 2 5 6输出
4
思路
LIS:给定一个长度为n的数组,找出一个最长的单调递增子序列。
例:序列A={5,6,7,4,2,8,3},它最长的单调递增子序列为{5,6,7,8},长度为4。
做法
定义状态dp[i]:表示以第i个数为结尾的最长递增子序列的长度。
状态转移方程:
最长的单调递增子序列:max {dp[i]}
复杂度: j在0~i之间滑动,复杂度O(n); i的变动范围也是O(n)的;总复杂度。
动态规划:复杂度
本题,DP代码提交到0J会超时。
DP不是LIS问题的最优解法,有复杂度0(nlogn)的非DP解法(二分查找)
本题题解:蓝桥杯刷题026——蓝桥骑士(二分法)
【例题】字符串转换
lanqiao0J题号1507
题目描述
小蓝拥有两个字符串 S,T。他希望通过如下操作使得字符 S 转换为字符串 T。
操作有一下三种:
- 删除一个字符。
- 插入一个字符。
- 将一个字符改为另一个字符。
问最少需要操作多少次才可以使得字符串 S 转换为字符串 T。
输入描述
输入第一行包含一个字符串 S。
输入第二行包含一个字符串 T。
1≤∣S∣,∣T∣≤2×10^3,保证 S、T 只包含小写字母。
输出描述
输出一个整数表示答案。
输入输出样例
输入
abc aa输出
2
数据范围在:1≤∣S∣,∣T∣≤ ,可以是
的复杂度
思路: 编辑距离
把长度m的A存储在数组a[1]~ a[m],长度为n的B存储在b[1]~ b[n],不用a[0]和b[0]。
定义状态dp: dp[i][j]表示A的前i个字符转换B的前j个字符所需要的操作次数
操作次数最少:dp[m][n]
下图是A="abcf",B="bcfe”的状态转移矩阵。
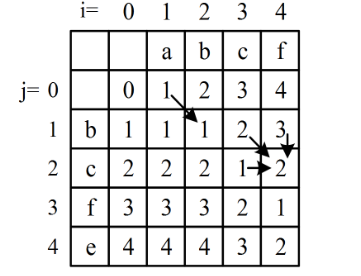
状态转移方程:
(1) 若a[i] = b[j],则dp[i][j] = dp[i-1][j-1]。例如图中dp[2][1]处的箭头
(2) 其他情况: dp[i][j] = min{dp[i-l][j-1],dp[i-1][j],dp[i][j-1]} + 1。例如图中dp[4][2]处的箭头。dp[i][j]是它左、左上、上的三个值中的最小值加1,分别对应以下操作:
- dp[i-1][j]+1,删除,将A的最后字符删除:
- dp[i][j-1]+1,插入,在B的最后插入A的最后字符:
- dp[i-1][j-1]+1,替换,将B的最后一个字符替换为A的最后一个字符。
复杂度:O(mn)
代码:
(1) a[i] = b[j],则dp[i][j] = dp[i-1][j-1]
(2)其他情况: dp[i][j] = min idp[i-1][j-1], dp[i-1][j], dp[i][j-1]} +1
a = input() ; a = ' '+a #a[0]不用,用a[1]~a[m]
b = input() ; b = ' '+b
m = len(a)-1
n = len(b)-1
dp = [[0]*(n + 1) for _ in range(m + 1)]
for i in range(1, m+1 ): dp[i][0] = i # 初始化
for j in range(1, n+1 ): dp[0][j] = j # 初始化
for i in range(1,m+1):for j in range(1, n+1):if a[i]==b[j]: dp[i][j] = dp[i-1][j-1]else:dp[i][j]=min(min(dp[i-1][j], dp[i][j-1]) , dp[i-1][j-1])+1
print(dp[m][n])
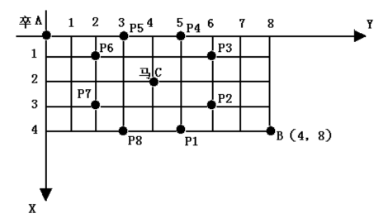
【例题】 过河卒
题目描述
如图,A 点有一个过河卒,需要走到目标 B 点。卒行走规则:可以向下、或者向右。同时在棋盘上的 C 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。
例如上图 C 点上的马可以控制 9 个点(图中的P1,P2,⋯P8 和 C)。卒不能通过对方马的控制点。棋盘用坐标表示,A 点(0,0)(0,0)、B 点(n,m)(1≤n,m ≤ 20),同样马的位置坐标是需要给出的。0≤马的坐标≤20。
现在要求你计算出卒从 A 点能够到达 B 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。。
输入描述
一行四个正整数,分别表示 B 点坐标和马的坐标。
输出描述
一个整数,表示所有的路径条数。
输入输出样例
输入
6 6 3 3输出
6
思路1:模拟
统计路径条数,看起来是个搜索题,可以用DFS求解。把马的控制点标记为不能走,绕过它们。不过,用DFS搜索的路径数量是天文数字,肯定超时。
思路2:网格上的DP
- 在小学上过奥数的都知道,这题应该用“标数法”,就是在每个坐标点上记录能走的路径条数。
- 标数法实际上就是DP的递推。
由于卒只能向下、或者向右移动,所以每个点(i, j)的路径条数等于能走到(i-1, j)的路径条数+能走到上边(i, j-1)的路径条数
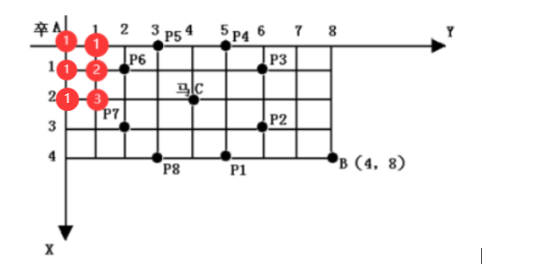
定义状态dp[ ][ ]: dp[i][j]表示卒走到坐标(i,j)时能走的路径条数。
如果不考虑马的控制点,有:dp[i]b]= dp[i - 1][j]+ dp[i][j - 1];
也就是(i, j)点的路径条数等于它上面和左边的路径条数之和。这就是小学奥数的“标数法”的原理。
本题的限制条件是马的控制点,只要令控制点的dp[i][j]=0(意思是卒走到该点时能走的路径条数为0)即可,即这个点上无路径。
代码:
小技巧:把坐标加2,防止马的控制点越界(坐标为负)
dp = [[0]*25 for i in range(25)]
s =[[0]*25 for i in range(25)]
bx,by,mx,my = map(int,input ().split())
bx += 2; by += 2; mx += 2; my += 2 # 把坐标加2
dp[2][1] = 1 # 初始化起始点的上面一点为1 起始点为(2,2)
s[mx][my] = 1; # 将马的9个控制点设置为1
s[mx-2][my-1]=1; s[mx-2][my+1]=1; s[mx+2][my-1]=1; s[mx+2][my+1]=1;
s[mx-1][my+2]=1; s[mx-1][my-2]=1; s[mx+1][my+2]=1; s[mx+1][my-2]=1;
for i in range(2,bx+1): # 从(2,2)开始for j in range(2,by+1):if s[i][j]==1: dp[i][j]=0 # 如果是马的控制点,则该点不能走else: dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
print(dp[bx][by]) # 到达终点B的路径条数【例题】 排队列
2019年国赛题
题目描述
在一个排列中,一个折点是指排列中的一个元素,它同时小于两边的元素,或者同时大于两边的元素。
对于一个 1 ∼ n 的排列,如果可以将这个排列中包含 t 个折点,则它称为一个 t+1 单调序列。
例如,排列 (1,4,2,3) 是一个 3 单调序列,其中 4 和 2 都是折点。
给定 n 和 k,请问 1 ∼ n 的所有排列中有多少个 k 单调队列?
输入描述
输入一行包含两个整数 n,k (1≤k≤n≤500)。
输出描述
输出一个整数,表示答案。答案可能很大,你可需要输出满足条件的排列数量除以 123456 的余数即可。
输入输出样例
输入
4 2输出
12
数据范围在1000左右,可以用复杂度为O(n^2)的算法。
方法一:暴力法
20%的测试:1<k<n<10
暴力法:对所有排列进行检查,判断是否为k单调队列。
from itertools import *
n,k = map(int,input().split())
nums = [i for i in range(1, n+1)] # 1~n
cnt = 0
for num in permutations (nums): # 检查每个排列tmp = 0for i in range(n-2): # 0 ~ n-3if num[i+1]>num[i+2] and num[i+1]>num[i]: tmp+=1 # 凸折点elif num[i+1]<num[i+2] and num[i+1]<num[i]: tmp+=1 # 凹折点if tmp == k-1 : cnt+=1
print(cnt %123456)方法二:DP
定义dp[ ][ ]: dp[i][i]表示序列包含1 ~i,且排列为j单调队列的方案数,也就是含有j-1个折点的方案数。
1 ∼ n 的所有排列中 k 单调队列的个数:dp[n][k]
状态转移方程:
从dp[i-1][]递推到dp[i][],把i插入到1 ~i-1的一个排列中,折点数量的变化:
dp[i][i] = dp [ i-1 ][ j ]*j+dp [ i-1 ][ j-1]*2+dp [ i-1 ][ j-2 ]*(i-j)
代码
N = 520
dp = [[0]*N for i in range(N)]
n,k = map(int,input ().split() )
dp[1][1] = 1
dp[2][1] = 2
for i in range(3, n+1):ki= min(k, i)for j in range (1,ki+1):dp[i][j] += dp[i-1][j]*j + dp[i-1][j-1]*2if j > 1: dp[i][j] += dp[i-1][j-2]*(i-j)
print(dp[n][k] % 123456)
【例题】砝码称重
2021年省赛题目
问题描述
你有一架天平和 N 个砝码,这 N 个砝码重量依次是
。
请你计算一共可以称出多少种不同的重量? 注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数 N。
第二行包含 N 个整数:
。
输出格式
输出一个整数代表答案。
对于所有评测用例,1≤N≤100,N个砝码总重不超过 100000。
样例输入
3 1 4 6样例输出
10样例说明
能称出的 10 种重量是:1、2、3、4、5、6、7、9、10、11。
1=1;
2=6−4(天平一边放 6,另一边放 4);
3=4−1;
4=4;
5=6−1;
6=6;
7=1+6;
9=4+6−1;
10=4+6;
11=1+4+6。
方法一:模拟
这一题也可以直接模拟,并且用set判重。
n = int (input ())
w = list (map(int,input ().split() ))
ans = set() # 用set判重,用来存用多少种答案的
ans.add(w[0])
for i in w[1:]:for j in ans.copy (): # ans.copy ()浅复制,不会因为该次循环而改变ansans.add(i) # 只放新砝码i的质量ans.add(j + i) # 将i和答案中每一个数放在同一侧:相加if j - i != 0: ans.add (abs(j - i)) # 将i和答案中每一个数放在不同测:相减
print (len(ans))
注意:对集合进行初始化时,不能直接ans = set(5),因为创建set()函数需要的是一个可迭代对象(如列表、元组、字符串等),而不能直接接受一个整型变量。所以集合初始化有两种方法:①创建空集合;②创建集合,赋予的参数必须是可迭代对象。如果我们需要在集合里添加一个元素,我们应该先创建空集合ans = set(),然后再ans.add(5)
set()是O(logn),两层循环是O(n*ans),所以总复杂度是O(n*ans*logn)
方法二:DP
建模:给定n个正整数,从中选出若个数字组合,每个数字可以加或者减,最终能得到多少种正整数结果。
DP状态定义: dp(i,j)表示前i个数字选择若干个加或者减,能否获得和为j。
DP状态转移方程: dp(i, j) = dp(i-1,j) l dp(i-1,j- wi) l dp(i-1, j+wi)
状态转移方程中有三种情况:
dp(i-1,j):不用第i个数字,和为j
dp(i-1, j -w):用第i个数字,且做减法,等价于用i-1个数字实现 j -Wi
dp(i-1,j+w;):用第i个数字,且做加法,等价于用i-1个数字实现 j+wi
代码:
n = int(input())
W = list(map(int, input().split()))
s = sum(W) # 所有砝码之和
dp = [[0] * (s + 1) for _ in range(n)]
for i, w in enumerate(W): # 初始化:前i个的砝码的质量为wdp[i][w] = 1
for i in range(1, n): # 第0行不需要管,因为只有一个质量for j in range(1, s+1):if dp[i - 1][j]: # 找到前i-1个可以组合出质量jdp[i][j] = 1 # 不选第i个,前i个也可以组合出质量jdp[i][j + W[i]] = 1 # 用第i个数字,且做加法if j != W[i] :dp[i][abs(j - W[i])] = 1 # 用第i个数字,且做减法
print(sum(dp[-1])) # dp[-1]就是dp的第一维的最后一个(即最后一行)通过90%测试。
对方法一:模拟进行优化
n = int (input ())
w = list (map(int,input ().split() ))
w.sort() # 从小到大排序,可以减少计算时间
ans = set() # 用set判重,用来存用多少种答案的
ans.add(w[0])
for i in w[1:]:for j in ans.copy (): # ans.copy ()浅复制,不会因为该次循环而改变ansans.add(i) # 只放新砝码i的质量ans.add(j + i) # 将i和答案中每一个数放在同一侧:相加ans.add (abs(j - i)) # 将i和答案中每一个数放在不同测:相减
# 判断是否质量为0放在两层for循环之外,减少时间复杂度
if 0 in ans: # 质量为0的不考虑ans.remove(0)
print (len(ans))
对方法二:DP进行优化
n = int(input())
W = list(map(int, input().split()))
W.sort() # 从小到大,减少时间复杂度
s = sum(W) # 所有砝码之和(最大值)
si = [sum(W[0:i]) for i in range(1,n+1)] # 质量W的前缀和
dp = [[0] * (s + 1) for _ in range(n)]
for i, w in enumerate(W): # 初始化:前i个的砝码的质量为wdp[i][w] = 1
for i in range(1, n): # 第0行不需要管,因为只有一个质量for j in range(1, si[i]+1):if dp[i - 1][j]: # 找到前i-1个可以组合出质量jdp[i][j] = 1 # 不选第i个,前i个也可以组合出质量jdp[i][j + W[i]] = 1 # 用第i个数字,且做加法dp[i][abs(j - W[i])] = 1 # 用第i个数字,且做减法
print(sum(dp[-1][1:])) # dp[-1]就是dp的第一维的最后一个(即最后一行)[1:]:不考虑质量为0的情况经过优化后的两段代码均通过100%测试。
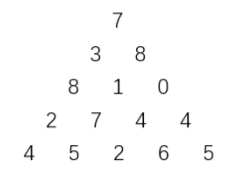
【例题】数字三角形
2020年省赛
题目描述
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。此外,向左下走的次数与向右下走的次数相差不能超过 1。
输入描述
输入的第一行包含一个整数 N (1≤N≤100),表示三角形的行数。
下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。
输出描述
输出一个整数,表示答案。
输入输出样例
输入
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5输出
27
思路
本题要求向左走的次数与向右走的次数差值不超过1,当到达最后一层时,一定是落在中间位置。
- 如果层数是奇数,最后一层落在正中间元素上,
- 如果层数是偶数,最后一层落在第N/2或第N/2+1个元素上。
定义状态dp[ ][ ],dp[i]i]表示从顶部到第i层横向第j个数,最大路径和。它只能从上一层的左边或右边转移而来。
代码
n = int(input())
a = [list (map(int, input ().split())) for i in range (n)] # 用来读取每行个数不同的元素
#数组a[][]同时当成dp[][]用
for i in range(1, n):for j in range (0, i + 1):if j == 0: a[i][j] += a[i-1][j] # 最左边元素elif j == i: a[i][j] += a[i-1][j-1] # 最右边元素else:a[i][j] += max(a[i-1][j-1 : j+1]) # 中间(从上面左边/从上面右边)
if n & 1: print(a[-1][n//2]) # 奇数行:在正中间
else: print (max(a[-1][n//2-1], a[-1][n//2])) # 偶数行:在正中间左边或者右边