剑指offer：关于二叉树的汇总（c++）

1、重建二叉树：

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

2、树的子结构：

输入两棵二叉树A和B，判断B是不是A的子结构。如图：A中有一部分子树的结构和B是一样的，因此B是A的子结构

#include<stdio.h>using namespace std;struct Node
{int value;//根节点BinaryTreeNode* m_pLeft;//左孩子BinaryTreeNode* m_pRight;//右孩子 
}//判断二叉树A是否包含二叉树B
//1->A;2->B
bool DoseTree1HaveTree2(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{//如果二叉树B节点全部遍历完，返回falseif(pRoot2 == NULL)return false;//如果遍历完二叉树A的全部结点，并且二叉树2未遍历结束，返回falseif(pRoot1 == NULL)return false;//如果遍历过程中有二叉树的结点不相同，遍历结束，返回falseif(pRoot1->value != pRoot2->value)return false;//递归遍历二叉树的所有左右子树return DoseTree1HaveTree2(pRoot1->m_pLeft, pRoot2->m_pLeft)&&DoseTree1HaveTree2(pRoot1->m_pRight, pRoot2->m_pRight);
}//判断两棵树的根结点是否相同
bool HasSubtree(BinaryTreeNode* pRoot1, BinaryTreeNode* pRoot2)
{bool result = false;if(pRoot1 != NULL && pRoot2 != NULL){//如果两个根节点相同，就是找到了if(pRoot1 ->value == pRoot2 ->value)result = DoseTree1HaveTree2(pRoot1,pRoot2);//如果未找到，则从左子树开始寻找if(!result) return = HasSubtree(pRoot1->m_pRight,pRoot2);//如果未找到，从右子树中查找if (!result)result = HasSubtree(pRoot1->m_pRight, pRoot2);}return result;
}

3、二叉树的镜像

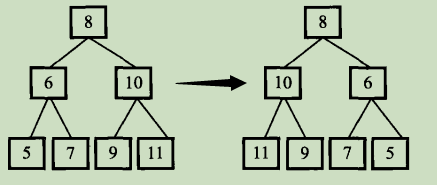
请完成一个函数，输入一个二叉树，该函数输出它的镜像。如图，右边的二叉树就是左边的树的镜像。

#include <iostream>struct BinaryTreeNode
{int  m_nValue;BinaryTreeNode*  m_pLeft;BinaryTreeNode*  m_pRight;
};// 生成二叉树镜像
void MirrorRecursively (BinaryTreeNode *pNode)
{//  如果结点为空，停止递归if (pNode == nullptr)return;//  交换左右子树std::swap(pNode->m_pLeft,pNode->m_pRight);//  当左子树非空时，递归生成左子树镜像if (pNode->m_pLeft)MirrorRecursively(pNode->m_pLeft);//  当右子树非空时，递归生成右子树镜像if (pNode->m_pRight)MirrorRecursively(pNode->m_pRight);
}int main()
{return EXIT_SUCCESS;
}

4、从上往下打印二叉树

从上往下打印出二叉树的每个结点，同一层的结点按照从左到右的顺序打印。

#include <iostream>
#include <queue>
using namespace std;struct BinaryTreeNode
{int value;BinaryTreeNode*m_pLeft;BinaryTreeNode*m_pRight;
};//从上往下打印
void PrintTree(BinaryTreeNode *pTreeRoot)
{if(pTreeRoot != NULL)return;queue<BinaryTreeNode *> queNode;queNode.push(pTreeRoot);while (!queNode.empty()){BinaryTreeNode *pNode =queNode.front();queNode.pop();cout << pNode->value << " ";if (pNode->p_left)queNode.push(pNode->p_left);if (pNode->p_right)queNode.push(pNode->p_right);}}int main()
{queue<BinaryTreeNode>data;BinaryTreeNode n1{5, nullptr, nullptr};BinaryTreeNode n2{7, nullptr, nullptr};BinaryTreeNode n3{9, nullptr, nullptr};BinaryTreeNode n4{11, nullptr, nullptr};BinaryTreeNode n5{6, &n1, &n2};BinaryTreeNode n6{10, &n3, &n4};BinaryTreeNode n7{8, &n5, &n6};PrintTree(&n7);return EXIT_SUCCESS;
}

5、二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。假设输入的数组的任意两个数字都互不相同

#include <iostream>
#include <queue>
using  namespace std;bool VerifySequenceOfBST(int sequence[], int length)
{if(sequence == NULL || length <= 0)return false;int root = length - 1;int i = 0;for(;i<length-1;++i){if(sequence[i] > root)break;}int j = i;for(;j<length-1;++j){if(sequence[j] < root)return false;}//只有当两个结点都为真才可以bool left = true;if (i > 0)left = VerifySequenceOfBST(sequence, i);bool right = true;if (i < length - 1)right = VerifySequenceOfBST(sequence + i, length - i - 1);return (left && right);
}int main()
{int binary_sort_tree[] = {5,7,6,9,11,10,8};cout << "The result is "<< VerifySequenceOfBST(binary_sort_tree, sizeof(binary_sort_tree)/ sizeof(int))          << endl;return EXIT_SUCCESS;
}

6、二叉树中和为某一值的路径

class Soultion
{puclic:vector<vector<int>>result;vector<int>tmp;vector<vector<int> > FindPath(TreeNode* root,int sum){if(root == NULL)return NULL;tmp.push_back(root->val);if(root->left == NULL && root->right && sum->root->val ==0)result.push_back(tmp);//如果不是父节点就是子节点FindPath(root->left,sum->root->val);FindPath(root->right,sum->root->val);if(tmp.size()>0)temp.pop_back();return result;}
};

7、二叉搜索树与双向链表

8、二叉树的深度

输入一棵二叉树的根结点，求该树的深度

思路：如果一棵树只有一个结点，它的深度为1。如果根结点只有左子树，那么树的深度应该是该其左子树的深度加1;同样如果根结点只有右子树而没有左子树，那么树的深度是其右子树的深度加1。如果既有右子树又有左子树，那该树的深度就是其左、右子树的深度较大值再加1。

头文件：

#include <iostream>
using namespace std;struct BinaryTreeNode
{int                 m_nValue;BinaryTreeNode*     m_pLeft;BinaryTreeNode*     m_pRight;
};

算法内容：

int TreeDepth(BinaryTreeNode* pRoot)
{if(pRoot == NULL)return;int nLeft = TreeDepth(pRoot->m_pLeft);int nRight = TreeDepth(pRoot->m_pRight);return (nLeft > nRight) ? (nLeft + 1) : (nRight + 1);
}

主函数：

int main()
{BinaryTreeNode n8{8, nullptr, nullptr};BinaryTreeNode n7{7, nullptr, nullptr};BinaryTreeNode n6{6, nullptr, nullptr};BinaryTreeNode n5{5, nullptr, nullptr};BinaryTreeNode n4{4, &n8, nullptr};BinaryTreeNode n3{3, &n6, &n7};BinaryTreeNode n2{2, &n4, &n5};BinaryTreeNode n1{1, &n2, &n3};int depth = 0;cout << "The depth is: " << TreeDepth(&n1) << endl<< "Is a Balance Tree ? : " << IsBalanced(&n1, &depth) << endl;return 0;
}

9、平衡二叉树

题目：输入一棵二叉树，判断该二叉树是否是平衡二叉树

思想：如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

class Solution
{ 
public:
bool IsBalanced_Solution(TreeNode* pRoot)
{if(pRoot == NULL)return true;int depth = 0;return IsBalanced(pRoot, &depth);
}private:
bool IsBalanced(TreeNode *pRoot, int *depth)
{if(pRoot == NULL){*depth =0;return true;}int left,right;if(IsBalanced(pRoot->left, &left) && IsBalanced(pRoot->right, &right)){int diff = left - right;if(diff <= 1 && diff >= -1){*depth = left>right?(left+1):(right+1);return true;}}return false;
}
};

10、二叉树的下一个结点

*/
/*分析二叉树的下一个节点，一共有以下情况：
1.二叉树为空，则返回空；
2.节点右孩子存在，则设置一个指针从该节点的右孩子出发，一直沿着指向左子结点的指针找到的叶子节点即为下一个节点；
3.节点不是根节点。如果该节点是其父节点的左孩子，则返回父节点；否则继续向上遍历其父节点的父节点，重复之前的判断，返回结果*/
class Solution {
public:TreeLinkNode* GetNext(TreeLinkNode* pNode){if(pNode==NULL)return NULL;if(pNode->right!=NULL){pNode = pNode->right;while(pNode->left){pNode = pNode->left;}return pNode;}while(pNode->next!=NULL){TreeLinkNode* proot = pNode->next;if(proot->left == pNode)return proot;pNode=pNode->next;}return NULL;}
};

11、对称的二叉树

题目：请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的

思路：递归判断：R1->left与R2->right比较，R2->left与R1->right比较

struct TreeNode
{int val;struct TreeNode *left;struct TreeNode *right;TreeNode(int x) :val(x), left(NULL), right(NULL) {}
};class Solution
{
public:
bool isSymmetrical(TreeNode* pRoot)
{return isSymmetrical(pRoot,pRoot);
}
private:
bool isSymmetrical(TreeNode *pRoot1, TreeNode *pRoot2)
{if(pRoot1 == NULL && pRoot2 == NULL){return true;}if(pRoot1 == NULL || pRoot2 == NULL){return false;}if(pRoot1->val != pRoot2->val){return false;}return isSymmetrical(pRoot->left, &right) && isSymmetrical(pRoot->right,&left);
}
};

12、按之字形顺序打印二叉树

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

13、把二叉树打印成多行

struct TreeNode
{int val;struct TreeNode*left;struct TreeNode*right;TreeNode(int x):val(x),left(NULL),right(NULL);{}
};class Solution
{public:vector<vector<int> > Print(TreeNode* pRoot){vector<vector<int>>ans;if(pRoot == NULL)return ans;queue<TreeNode*>q;q.push(pRoot);while(q.empty()){int size = q.size();//读取每一层的元素的数量vector<TreeNode*>q1;while(size--){TreeNode*front = q.front();q.pop();q1.push_back(front ->val);if(front->left!=NULL) return front->left;if(front->right!=NULL) return front->right;}ans.push_back(q1);}return ans;}
};

14、序列化二叉树

15、二叉搜索树的第k个结点

//中序遍历
TreeNode* KthNode(TreeNode* pRoot, unsigned int k)
{TreeNode *cur = root;int count = 0;stack<TreeNode*>s;while(s.empty() || cur){if(cur != NULL){s.push(cur);cur = cur->left;}else{cur = s.top();s.pop();count++;if(num == k)return cur->val;cur = cur->right;}}return 0;
}