【数据结构与算法分析inC-MarkAllen】1-数学基础

文章目录
- 1. 第一章
-
- 1.1 进行算法分析目的
-
- 1.1.1 适应大量数据情况
-
- 从 NNN 个数中选择第 kkk 大的数
-
- 递减排序,取第K大的数
- 插入排序思想
- 1.1.2 边界条件正确
- 1.2 数学知识复习
-
- 1.2.1 指数
- 1.2.2 对数
- 1.2.3 级数
-
- 几何级数
- 算术级数
- 1.2.4 模运算
-
- 性质
- 1.2.5 证明方法
-
- 归纳法
-
- 斐波那契
- 反证法
- 1.3 递归简论
- 练习题
数据结构研究组织大量数据的方法,算法分析是对算法运行时间的评估
1. 第一章
在程序正确运行前提下,保证在大量数据集或者特殊情况下能够运行并得出正确结果
1.1 进行算法分析目的
1.1.1 适应大量数据情况
由于简单选择排序,冒泡排序,插入排序的时间复杂度都是 O(n2)O(n^2)O(n2) 。只要基于此思想,时间复杂度都不会低,如后例:
从 NNN 个数中选择第 kkk 大的数
递减排序,取第K大的数
冒泡排序
//对全部数据进行冒泡排序
void Bubble_Sort(int a[],int n){bool flag = false;for(int i = 1;i <= n;++i){for(int j = 1;j <= n-i;++j){if(a[j] < a[j+1]){swap(a[j],a[j+1]);flag = true;}}if(flag == false)return ;}
}void Select_Sort(int a[],int n){for(int i = 1;i <= n;i++){int maxIdx = i;for(int j = i+1;j <= n;++j){if(a[j] > a[maxIdx])maxIdx = j;}if(maxIdx != i)swap(a[maxIdx],a[i]);}
}void KBig(int a[],int n,int k){//先排序Bubble_Sort(a,n);Select_Sort(a,n);return a[k];
}
插入排序思想
取前 KKK个数递减排序。再取新数 xix_ixi ,从第一个数开始比较
- xi≥aix_i \\ge a_ixi≥ai :则将该数插入
- xi<akx_i < a_kxi<ak :则不做操作
//从小到大排序
void Direct_InsertSort(ElemType A[], int k){int i,j;for(i = 2;i <= k;++i){if(A[i] > A[i-1]){//若待插入元素A[i] > A[i-1] ,从后向前找插入位置A[0] = A[i];//A为一固定序列,且数据存储已定,所以需要哨兵记录待插入元素 for(j = i-1;j >= 0 && A[0] > A[j];--j)A[j+1] = A[j];A[j+1] = A[0];}}
}int KBig_Insert(int a[],int n,int k){///sort(a,k);//将前k个数据降序排序Direct_InsertSort(a,k);for(int i = k+1;i <= n;++i){if(a[i] > a[k]){a[0] = a[i];for(int j = k;j >= 0 && a[0] > a[j];--j)a[j+1] = a[j];a[j+1] = a[0];}}return a[k];//处理完全部数据后,第k个数据为所求
}int main(){int n;//输入n省略int a = (int *)malloc(sizeof(int)*(n+1));for(int i = 1;i <= n;++i){//初始化n个数据...}KBig_Insert(a,n,k);return 0;
}
1.1.2 边界条件正确
1.2 数学知识复习
1.2.1 指数
XAXB=XA+BX^AX^B=X^{A+B} XAXB=XA+B
XAXB=XA−B\\frac{X^A}{X^B}=X^{A-B} XBXA=XA−B
(XA)B=XAB(X^{A})^B=X^{AB} (XA)B=XAB
XN+XN=2XNX^N+X^N=2X^N XN+XN=2XN
1.2.2 对数
在计算机中,除非特别声明,所有对数都是以2为底的
logAB=logCBlogCA;C>0log_AB=\\frac{log_CB}{log_CA};C>0 logAB=logCAlogCB;C>0
logAB=logA+logBlogAB=logA+logB logAB=logA+logB
logAB=logA−logBlog\\frac{A}{B}=logA-logB logBA=logA−logB
log(AB)=BlogAlog(A^B)=BlogA log(AB)=BlogA
logX<X,X>0logX<X,X>0 logX<X,X>0
log1=0,log2=1,log1024=10log1=0,log2=1,log1024=10 log1=0,log2=1,log1024=10
1.2.3 级数
几何级数
有是否收敛的区别
由等比数列求和
∑i=0NAi=1−AN+11−A,0<A<1,当N→∞时,收敛于11−A\\sum_{i=0}^NA^i=\\frac{1-A^{N+1}}{1-A},0<A<1,当 N\\rightarrow \\infty 时,收敛于 \\frac{1}{1-A} i=0∑NAi=1−A1−AN+1,0<A<1,当N→∞时,收敛于1−A1
证明:
S=1+A+A2+⋯AS=A+A2+A3+⋯S−AS=1⇒S=11−A\\begin{aligned} &S=1+A+A^2+\\cdots\\\\ &AS=A+A^2+A^3+\\cdots\\\\ &S-AS=1\\Rightarrow S=\\frac{1}{1-A} \\end{aligned} S=1+A+A2+⋯AS=A+A2+A3+⋯S−AS=1⇒S=1−A1
∑i=1∞i2i=2\\sum_{i=1}^\\infty \\frac{i}{2^i}=2 i=1∑∞2ii=2
证明:
S=12+222+323+⋯2S=1+22+222+⋯2S−S=1+1⇒S=2\\begin{aligned} &S=\\frac{1}{2}+\\frac{2}{2^2}+\\frac{3}{2^3}+\\cdots\\\\ &2S=1+\\frac{2}{2}+\\frac{2}{2^2}+\\cdots\\\\ &2S-S=1+1\\Rightarrow S=2 \\end{aligned} S=21+222+233+⋯2S=1+22+222+⋯2S−S=1+1⇒S=2
算术级数
可以通过基本公式计算值
∑i=1Ni=(1+N)N2≈N2∑i=1Ni2=N(N+1)(2N+1)6≈N33⋮∑i=1nik=Nk+1∣k+1∣,k≠−1对于k=−1,调和数HN=∑i=1N1i=logeN\\begin{aligned} &\\sum_{i=1}^N i=\\frac{(1+N) N}{2}\\approx\\frac{N}{2}\\\\ &\\sum_{i=1}^Ni^2=\\frac{N(N+1)(2N+1)}{6}\\approx\\frac{N^3}{3}\\\\ &\\vdots\\\\ &\\sum_{i=1}^ni^k=\\frac{N^{k+1}}{\\vert k+1\\vert},k\\neq -1\\\\ &对于k=-1,调和数H_N=\\sum_{i=1}^N\\frac{1}{i}=log_eN \\end{aligned} i=1∑Ni=2(1+N)N≈2Ni=1∑Ni2=6N(N+1)(2N+1)≈3N3⋮i=1∑nik=∣k+1∣Nk+1,k=−1对于k=−1,调和数HN=i=1∑Ni1=logeN
SP:
∑i=1Nf(N)=Nf(N)∑i=n0Nf(i)=∑i=1Nf(i)−∑i=n1n0−1f(i)\\begin{aligned} &\\sum_{i=1}^Nf(N)=N f(N)\\\\ &\\sum_{i=n_0}^N f(i)= \\sum_{i=1}^{N}f(i)-\\sum_{i=n_1}^{n_0-1}f(i) \\end{aligned} i=1∑Nf(N)=Nf(N)i=n0∑Nf(i)=i=1∑Nf(i)−i=n1∑n0−1f(i)
1.2.4 模运算
A与B模N同余,记为 A≡B(modN)A\\equiv B(mod\\quad N)A≡B(modN) 如: 81≡61≡1(mod10)81\\equiv 61\\equiv 1(mod\\quad 10)81≡61≡1(mod10)
性质
A≡B(modN)⇒(A+C)≡(B+C)(modN)⇒AD≡BD(modN)\\begin{aligned} A\\equiv B(mod N)&\\Rightarrow (A+C)\\equiv(B+C)(mod\\quad N)\\\\ &\\Rightarrow AD\\equiv BD(mod\\quad N) \\end{aligned} A≡B(modN)⇒(A+C)≡(B+C)(modN)⇒AD≡BD(modN)
1.2.5 证明方法
归纳法
- 证明基准情形
- 归纳假设:假设定力对直到某个有限数k的所有情况都成立,在通过这个假设证明后续值成立。
斐波那契
{F0=1,F1=1Fi=Fi−1+Fi−2,i≥2\\begin{cases} &F_0=1,F_1=1\\\\ &F_i=F_{i-1}+F_{i-2},i\\ge 2 \\end{cases} {F0=1,F1=1Fi=Fi−1+Fi−2,i≥2
证明:Fk+1<(53)k+1F_{k+1}< \\left(\\frac{5}{3}\\right)^{k+1}Fk+1<(35)k+1 证明:
当k=0时,F1=1<53,则在k=0时成立假设k=m−1时,有Fm<(53)m成立则当k=m时,Fm+1<(53)m+(53)m−1<(35)(53)m+1+(35)2(53)m+1<(35+925)(53)m+1=2425(53)m+1<(53)m+1\\begin{aligned} &当k=0时,F_1=1<\\frac{5}{3},则在k=0时成立\\\\ &假设k=m-1时,有F_{m}< \\left(\\frac{5}{3}\\right)^{m}成立\\\\ &则当k=m时,F_{m+1}< \\left(\\frac{5}{3}\\right)^{m}+\\left(\\frac{5}{3}\\right)^{m-1}<\\left(\\frac{3}{5}\\right)\\left(\\frac{5}{3}\\right)^{m+1}+\\left(\\frac{3}{5}\\right)^2\\left(\\frac{5}{3}\\right)^{m+1}\\\\ &<\\left(\\frac{3}{5}+\\frac{9}{25}\\right)\\left(\\frac{5}{3}\\right)^{m+1}=\\frac{24}{25}\\left(\\frac{5}{3}\\right)^{m+1}<\\left(\\frac{5}{3}\\right)^{m+1} \\end{aligned} 当k=0时,F1=1<35,则在k=0时成立假设k=m−1时,有Fm<(35)m成立则当k=m时,Fm+1<(35)m+(35)m−1<(53)(35)m+1+(53)2(35)m+1<(53+259)(35)m+1=2524(35)m+1<(35)m+1
反证法
1.3 递归简论
四条基本法则
- 基准情形:某些基准情形,无需递归就能解出
- 不断推进:每次递归调用,必须向基准情形推进(不能出现循环定义)
- 设计法则:假设所有递归调用都能运行
- 合成效益法则:不同递归调用做不同的工作
void printOut(unsigned int N){if(N >= 10)printOut(N/10);// printDight(n)表示将单个数字输出到显示终端printDigit(N-(N/10)*10);//printDigit(N%10);
}
- 取模运算耗费很大?
练习题
1.3 只使用处理IO的 PrintDigit 函数,编写一个可以输出任意实数的函数
由于实数用计算机表示会存在舍入误差(RoundUp),所以在输出前,需按照舍入策略进行舍入。
-
事前指定小数点后保留
DecPlaces位 -
舍入策略为四舍五入
小数点后第
DecPlace+1位加 0.5×10−DecPlaces0.5\\times 10^{-DecPlaces}0.5×10−DecPlaces
# include<iostream>using namespace std;//四舍五入
double RoundUp(double N,int DecPlaces){int i;double AmountToAdd = 0.5;//小数点后移 DecPlaces 位for(i = 0;i < DecPlaces;++i)AmountToAdd /= 10;return N+AmountToAdd;
}//输出小数部分
void PrintFractionPart(double FractionPart,int DecPlaces){int i,ADigit;for(i = 0;i < DecPlaces;++i){FractionPart *= 10;//小数点后第一位移到个位ADigit = (int)FractionPart;//输出个位,即小数点后第一位cout << ADigit;FractionPart = FractionPart - ADigit;//递归输出后续小数部分}
}void PrintReal(double N,int DecPlaces){int IntPart;double FractionPart;if(N < 0){putchar('-');N = -N;}N = RoundUp(N,DecPlaces);//四舍五入IntPart = (int)N;FractionPart = N-IntPart;//获取小数部分cout << IntPart;if(DecPlaces > 0)putchar('.');PrintFractionPart(FractionPart,DecPlaces);
}int main(){cout << "输入需要输出的实数:";double N;cin >> N;cout << "输入小数点后位数:";int DecPlaces;//精度cin >> DecPlaces;PrintReal(N,DecPlaces);return 0;
}
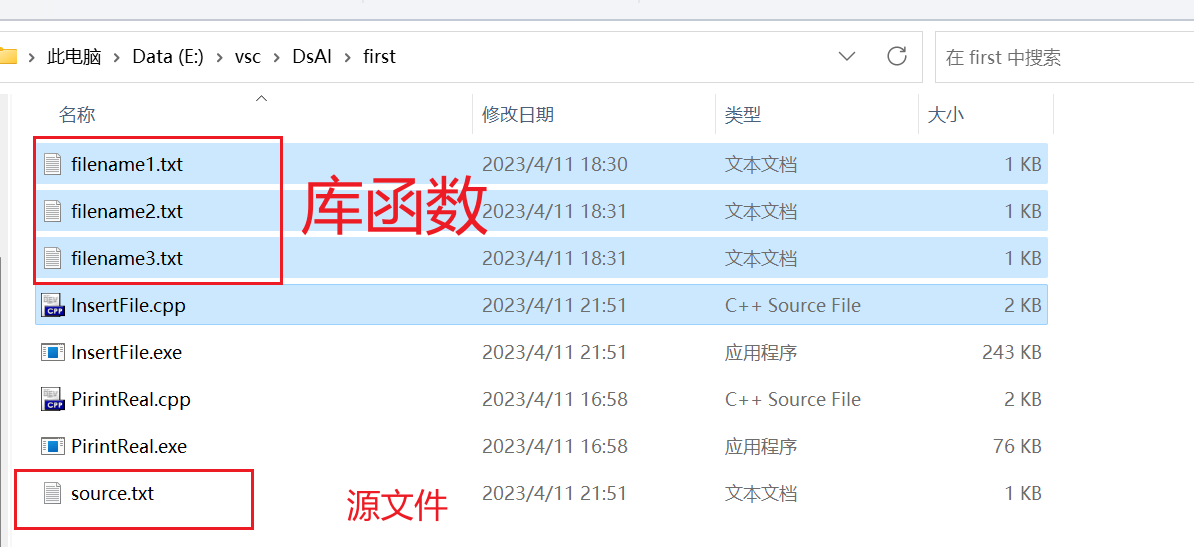
1.4 语言提供 #include filename 的语句,用于读入 filename ,并将它插入到 include 语句处
- 文件本身还可以包含
#include语句- 不能
include自身(self-referential)
- 不能
思路:
-
逐行检测源代码,是否存在
#include SomeFile -
检查
list中,是否有文件名SomeFile- 有,则
continue - 无:
- 调用
ProcessFile(SomeFile);,将文件内容插入当前位置; - 将
SomeFile入list
- 调用
list列表,维护由ProcessFile处理过的文件,避免重复调用 - 有,则
# include<iostream>
# include<cstdio>
#include<algorithm>
#include<vector>using namespace std;int main(int argc, char const *argv[]){/* code */FILE *fp = fopen("source.txt", "w+");fputs("#include <filename1>\\n", fp);fputs("#include <filename1>\\n", fp);fputs("#include <filename2>\\n", fp);fputs("#include <filename3>\\n", fp);fputs("#include <filename3>\\n", fp);fputs("\\n", fp);fputs("int main(){\\n", fp);fputs(" cout << 'Hello' <<endl;\\n", fp);fputs(" return 0;\\n", fp);fputs("};\\n", fp);rewind(fp);vector<string> list;char str[1024];char st[1024];string tmp;while(fgets(str, 1024, fp) && !feof(fp)){tmp = str;//去除空格tmp.erase(remove_if(tmp.begin(), tmp.end(), [](char c) {return (c == ' ');}), tmp.end());//网上找的,之后再说if('#' == str[0]){string filename = tmp.substr(tmp.find('<')+1,tmp.find('>')-tmp.find('<')-1);//str.substr(beginIdx,len)vector<string>::iterator idx = find(list.begin(),list.end(),filename);if(list.end() == idx){cout << str;// cout << filename << endl;list.push_back(filename);//ProcessFile(filename);查找filename文件,将其插入当前位置FILE *fo = fopen((filename+".txt").data(), "r");while(fgets(st, 1024, fo)){string stt = st;cout << stt;}cout << endl;}else{continue;}}else{cout << str;}}fclose(fp);return 0;
}

1.5 证明公式
log2X<Xlog_2X<Xlog2X<X 对所有 X>0X>0X>0 成立
证明:
| logXlogXlogX | XXX | |
|---|---|---|
| (0,1](0,1](0,1] | ≤0\\le 0≤0 | >0>0>0 |
| (1,2](1,2](1,2] | ≤1\\le 1≤1 | >1 |
| (2,4](2,4](2,4] | ≤2\\le 2≤2 | >2>2>2 |
| (p,2p](p,2p](p,2p] | ≤p\\le p≤p | >p>p>p |
对于logY=log(2×Y2)=1+logY2<1+Y2≤Y2+Y2=Y⇒log2Y<Y\\begin{aligned} &对于logY=log(2\\times \\frac{Y}{2})=1+log\\frac{Y}{2}<1+\\frac{Y}{2}\\le \\frac{Y}{2}+\\frac{Y}{2}=Y\\Rightarrow log_2Y<Y \\end{aligned} 对于logY=log(2×2Y)=1+log2Y<1+2Y≤2Y+2Y=Y⇒log2Y<Y
1.6 级数求和
∑i=0∞14i\\sum_{i=0}^{\\infty}\\limits \\frac{1}{4^i}i=0∑∞4i1
S=∑i=0∞14i=1+14+142+⋯,4S=∑i=0∞44i=4+1+442+⋯=4+1+14+⋯3S=4S−S=4⇒S=43\\begin{aligned} &S=\\sum_{i=0}^{\\infty}\\limits \\frac{1}{4^i}=1+\\frac{1}{4}+\\frac{1}{4^2}+\\cdots, 4S=\\sum_{i=0}^{\\infty}\\limits \\frac{4}{4^i}=4+1+\\frac{4}{4^2}+\\cdots=4+1+\\frac{1}{4}+\\cdots\\\\ &3S=4S-S=4\\Rightarrow S=\\frac{4}{3} \\end{aligned} S=i=0∑∞4i1=1+41+421+⋯,4S=i=0∑∞4i4=4+1+424+⋯=4+1+41+⋯3S=4S−S=4⇒S=34
∑i=0∞i4i\\sum_{i=0}^{\\infty}\\limits \\frac{i}{4^i}i=0∑∞4ii
S=∑i=0∞i4i=14+242+343+⋯,4S=∑i=0∞i4i=1+24+342+⋯3S=1+14+142+⋯=43⇒S=49\\begin{aligned} &S=\\sum_{i=0}^{\\infty}\\limits \\frac{i}{4^i}=\\frac{1}{4}+\\frac{2}{4^2}+\\frac{3}{4^3}+\\cdots,4S=\\sum_{i=0}^{\\infty}\\limits \\frac{i}{4^i}=1+\\frac{2}{4}+\\frac{3}{4^2}+\\cdots\\\\ &3S=1+\\frac{1}{4}+\\frac{1}{4^2}+\\cdots=\\frac{4}{3}\\Rightarrow S=\\frac{4}{9} \\end{aligned} S=i=0∑∞4ii=41+422+433+⋯,4S=i=0∑∞4ii=1+42+423+⋯3S=1+41+421+⋯=34⇒S=94
∑i=0∞i24i\\sum_{i=0}^{\\infty}\\limits \\frac{i^2}{4^i}i=0∑∞4ii2
S=∑i=0∞i24i=14+442+943+⋯,4S=1+1+942+⋯3S=1+34+542+⋯+2i+14i+⋯=∑i=0∞14i+2∑i=0∞i42=43+89=209\\begin{aligned} &S=\\sum_{i=0}^{\\infty}\\limits \\frac{i^2}{4^i}=\\frac{1}{4}+\\frac{4}{4^2}+\\frac{9}{4^3}+\\cdots,4S=1+1+\\frac{9}{4^2}+\\cdots\\\\ &3S=1+\\frac{3}{4}+\\frac{5}{4^2}+\\cdots+\\frac{2i+1}{4^i}+\\cdots=\\sum_{i=0}^{\\infty}\\limits\\frac{1}{4^i}+2\\sum_{i=0}^{\\infty}\\frac{i}{4^2}=\\frac{4}{3}+\\frac{8}{9}=\\frac{20}{9} \\end{aligned} S=i=0∑∞4ii2=41+424+439+⋯,4S=1+1+429+⋯3S=1+43+425+⋯+4i2i+1+⋯=i=0∑∞4i1+2i=0∑∞42i=34+98=920
d. 太复杂,思路就是上述解法不断迭代
1.7 估计∑i=⌊N2⌋N1i\\sum_{i=\\lfloor\\frac{N}{2}\\rfloor}^N\\limits\\frac{1}{i}i=⌊2N⌋∑Ni1
S=∑i=1N−∑1i=⌊N2⌋−11i=lnN−lnN2≈ln2S=\\sum_{i=1}^N-\\sum_1^{i=\\lfloor\\frac{N}{2}\\rfloor-1}\\limits\\frac{1}{i}=lnN-ln\\frac{N}{2}\\approx ln2S=∑i=1N−1∑i=⌊2N⌋−1i1=lnN−ln2N≈ln2
1.8 2100(mod5)2^{100}\\left(mod\\quad5\\right)2100(mod5)
21(mod5)=2,22(mod5)=4,23(mod5)=3,24(mod5)=1,25(mod5)=22100(mod5)=(24)25(mod5)=1\\begin{aligned} &2^1\\left(mod\\quad5\\right)=2,\\quad2^2\\left(mod\\quad5\\right)=4, \\quad 2^3\\left(mod\\quad5\\right)=3,\\quad2^4\\left(mod\\quad5\\right)=1,\\quad 2^5\\left(mod\\quad5\\right)=2\\\\ &2^{100}\\left(mod\\quad 5\\right)=\\left(2^{4}\\right)^{25}\\left(mod\\quad 5\\right)=1 \\end{aligned} 21(mod5)=2,22(mod5)=4,23(mod5)=3,24(mod5)=1,25(mod5)=22100(mod5)=(24)25(mod5)=1
1.9 令 FiF_iFi 为斐波那契数,证明
F0=1,F1=1,F2=2,Fm=Fm−1+Fm−2F_0=1,F_1=1,F_2=2,F_m=F_{m-1}+F_{m-2}F0=1,F1=1,F2=2,Fm=Fm−1+Fm−2
∑i=1N−2Fi=FN−2\\sum_{i=1}^{N-2}\\limits F_i=F_N-2i=1∑N−2Fi=FN−2
归纳法:
N=3时,F1=1,F3−2=1=F1,等式成立假设N=m时,有∑i=1m−2Fi=Fm−2当N=m+1时,∑i=1m−1Fi=Fm−1+∑i=1m−2Fi=Fm−1+Fm−2=Fm+1−2,等式成立\\begin{aligned} &N=3时,F_1=1,F_3-2=1=F_1,等式成立\\\\ &假设N=m时,有\\sum_{i=1}^{m-2}\\limits F_i=F_m-2\\\\ &当N=m+1时,\\sum_{i=1}^{m-1}\\limits F_i=F_{m-1}+\\sum_{i=1}^{m-2}F_i=F_{m-1}+F_m-2=F_{m+1}-2,等式成立 \\end{aligned} N=3时,F1=1,F3−2=1=F1,等式成立假设N=m时,有i=1∑m−2Fi=Fm−2当N=m+1时,i=1∑m−1Fi=Fm−1+i=1∑m−2Fi=Fm−1+Fm−2=Fm+1−2,等式成立
FN<ϕN,其中ϕ=1+52F_N<\\phi^N,其中\\phi=\\frac{1+\\sqrt{5}}{2}FN<ϕN,其中ϕ=21+5
ϕ2=1+5+254=3+52=1+ϕ⇒1=1ϕ+1ϕ2当N=1时,F1=1,ϕ>F1假设,当N<k,有FN<ϕN成立,当N=k+1时,Fk+1=Fk+Fk−1<ϕk+ϕk−1=ϕk+1(1ϕ+1ϕ2)=ϕk+1等式成立\\begin{aligned} &\\phi^2=\\frac{1+5+2\\sqrt{5}}{4}=\\frac{3+\\sqrt{5}}{2}=1+\\phi\\Rightarrow 1=\\frac{1}{\\phi}+\\frac{1}{\\phi^2}\\\\ &当N=1时,F_1=1,\\phi>F_1\\\\ &假设,当N<k,有F_N<\\phi^N成立,\\\\ &当N=k+1时,F_{k+1}=F_{k}+F_{k-1}<\\phi^{k}+\\phi^{k-1}=\\phi^{k+1}\\left(\\frac{1}{\\phi}+\\frac{1}{\\phi^2}\\right)=\\phi^{k+1}\\\\ &等式成立 \\end{aligned} ϕ2=41+5+25=23+5=1+ϕ⇒1=ϕ1+ϕ21当N=1时,F1=1,ϕ>F1假设,当N<k,有FN<ϕN成立,当N=k+1时,Fk+1=Fk+Fk−1<ϕk+ϕk−1=ϕk+1(ϕ1+ϕ21)=ϕk+1等式成立
1.10 证明公式
∑i=1N(2i−1)=N2\\sum_{i=1}^{N}\\limits(2i-1)=N^2i=1∑N(2i−1)=N2
∑i=1N(2i−1)=2∑i=1Ni−∑i=1N1=N(N+1)−N=N2\\begin{aligned} &\\sum_{i=1}^{N}\\limits(2i-1)=2\\sum_{i=1}^{N}\\limits i-\\sum_{i=1}^{N}\\limits1=N(N+1)-N=N^2 \\end{aligned} i=1∑N(2i−1)=2i=1∑Ni−i=1∑N1=N(N+1)−N=N2
∑i=1Ni3=(∑i=1Ni)2\\sum_{i=1}^{N}\\limits i^3=\\left(\\sum_{i=1}^N\\limits i\\right)^2i=1∑Ni3=(i=1∑Ni)2
归纳法证明:
N=1时,等式成立假设N=N时,有等式∑i=1Ni3=(∑i=1Ni)2成立∑i=1N+1i3=(N+1)3+∑i=1Ni3=(N+1)3+N2(N+1)24=[(N+1)(N+2)2]2=[∑i=1N+1i]2可知N=N+1时,等式成立,故上述等式成立\\begin{aligned} &N=1时,等式成立\\\\ &假设N=N时,有等式\\sum_{i=1}^{N}\\limits i^3=\\left(\\sum_{i=1}^N\\limits i\\right)^2 成立\\\\ &\\sum_{i=1}^{N+1}i^3=(N+1)^3+\\sum_{i=1}^Ni^{3}=(N+1)^3+\\frac{N^2(N+1)^2}{4}=\\left[\\frac{(N+1)(N+2)}{2}\\right]^2=\\left[\\sum_{i=1}^{N+1}i\\right]^2\\\\ &可知N=N+1时,等式成立,故上述等式成立 \\end{aligned} N=1时,等式成立假设N=N时,有等式i=1∑Ni3=(i=1∑Ni)2成立i=1∑N+1i3=(N+1)3+i=1∑Ni3=(N+1)3+4N2(N+1)2=[2(N+1)(N+2)]2=[i=1∑N+1i]2可知N=N+1时,等式成立,故上述等式成立


