SVM支持向量机理解_KKT条件_拉格朗日对偶_SMO算法

目录
一、支持向量机基本型(线性可分)
1.1 问题描述
1.2 参考资料
二、KKT条件
2.1 KKT条件的几个部分
2.1.1 原始条件
2.1.2 梯度条件
2.1.3 松弛互补条件
2.2 参考资料
三、对偶形式
四、SMO算法
五、线性不可分情形
六、核函数
一、支持向量机基本型(线性可分)
1.1 问题描述
在PLA感知机算法中我们求取超平面是保证所有目标分类正确即可,但是我们为了增加我们学习到的算法的鲁棒性,泛化能力更强,我们可以使超平面到样本的间隔距离最大,这里我们定义间隔为“样本到超平面的最近距离”,也就是说我们的超平面就是对应间隔最大的平面。下面我们用数学语言来描述。
假设样本集,设超平面为
,点到超平面的距离
,最小间隔则为
,当
达到最大时的
就对应我们的超平面。即:
现在的问题转变成了优化问题。
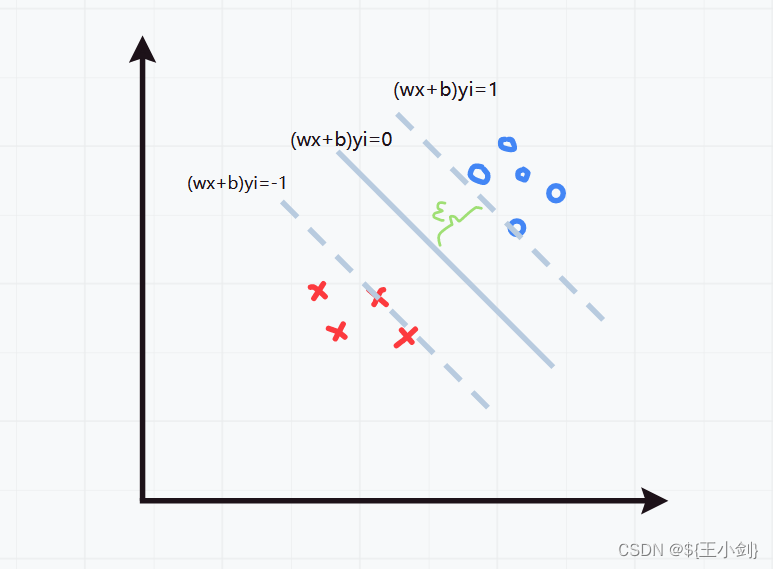
对于这样确定的,必然存在
,
,即:
对进行缩放是不影响超平面的,所以可以必然存在这样的
,使得:
//这个式子隐含了
这个条件了
所以:
要使达到最大,则使
最小即可。所以上述优化问题可以写成下列形式:
1.2 参考资料
以上就是支持向量机的基本型。详细内容可参见李航《机器学习方法》第七章支持向量机。网上其他参考资料可参见:
文档资料:
机器学习:支持向量机(SVM)_燕双嘤的博客-CSDN博客_支持向量机
支持向量机通俗导论(理解SVM的三层境界)_v_JULY_v的博客-CSDN博客_支持向量机
视频资料:
推导SVM基本形式_哔哩哔哩_bilibili
【数之道25】机器学习必经之路-SVM支持向量机的数学精华_哔哩哔哩_bilibili
1. 支持向量机(线性模型)问题_哔哩哔哩_bilibili
svm原理推导:1-支持向量机要解决的问题_哔哩哔哩_bilibili
二、KKT条件
我把KKT条件放到第二节来讲,我觉得更加符合我们的思维方式,在第一节中我们给出了SVM的基本型,那么接下来我们来试图求解这个优化问题,由此引出KKT条件,很多写法将KKT条件直接上来就构建拉格朗日辅助函数,然后就给读者说就是这么回事,这种逻辑其实不合理,应当直接从梯度角度来讲这个事情。
2.1 KKT条件的几个部分
上述优化问题:
2.1.1 原始条件
2.1.2 梯度条件
在求解带不等式约束的优化问题时,考虑两种情况一种是不等式约束有效,一种是不等式约束无效。我们把要优化的函数称为目标函数(这个地方只考虑凸函数的情况)。
(1)当约束条件无效时,目标函数最优值为其梯度为0时的值。
(2)当约束条件有效时(目标函数不在约束范围内),那么目标函数取得最优值是应当与约束条件“相切”,也就是梯度方向成平行关系,具体可分为以下4种情况,我们假设目标函数为,约束函数为
:
1.

此时有:
2.
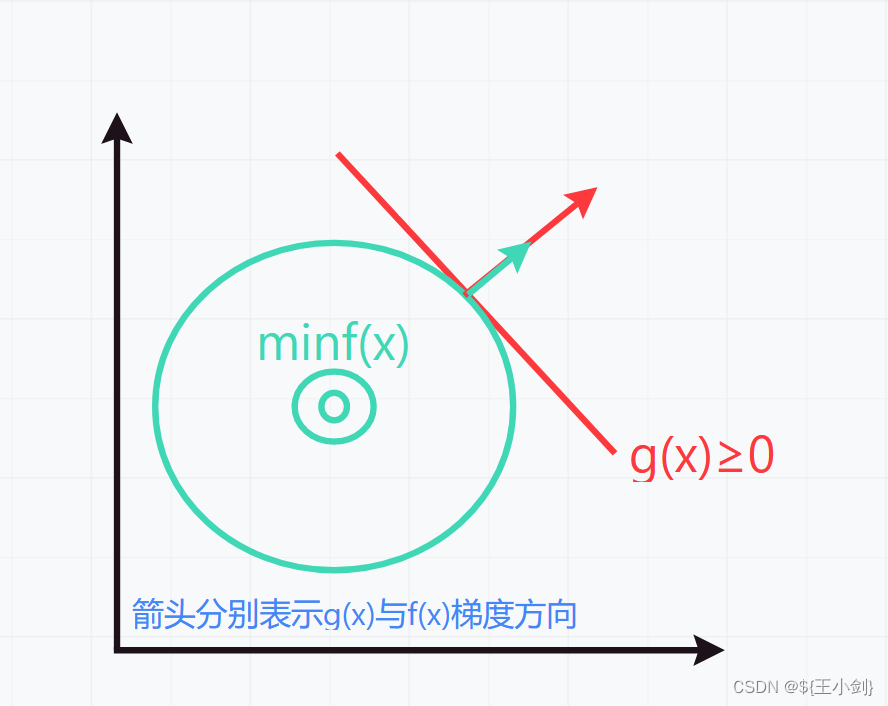
此时有:
3.
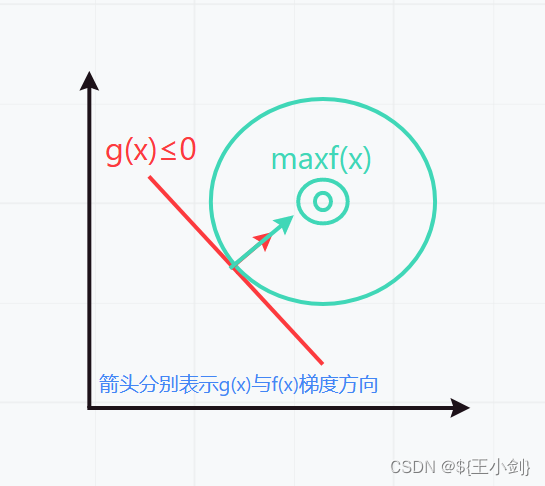
此时有:
4.
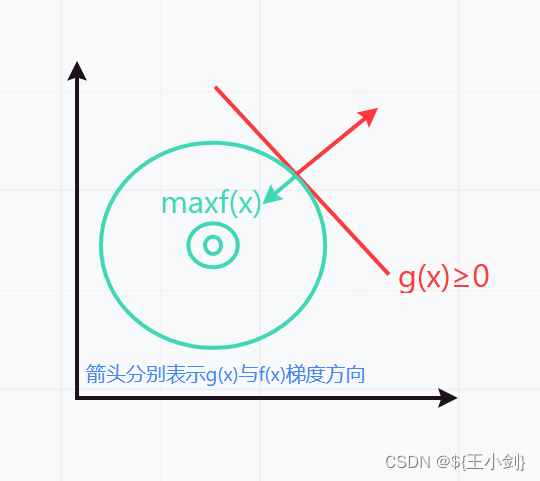
此时有:
注意的梯度方向与
具体函数相关,这里为了举例方便仅画出示意图默认了梯度方向。
在SVM基本型的优化问题中,其情形属于第二种情况,即:
综上两种情况可知:
或
由于原优化问题是多约束条件,我们画出示意图如下:
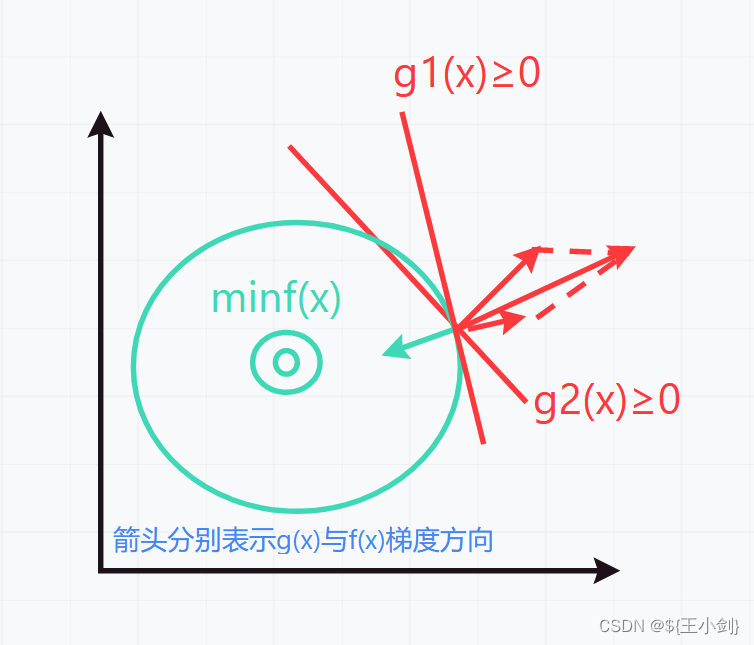
此时有:
综上所述,代入原式子,即:
或
为了将两种情况综合到一起,我们引入了互补松弛条件。
2.1.3 松弛互补条件
我们把约束条件有效和约束条件无效两种情况综合打一起,实际上对于第二种情况,当约束条件无效时,可令对应的乘子
=0,此时第二种情况也就变成了第一种情况,当约束条件有效时则约束条件
=0,所有始终有:
我们称之为互补松弛条件。
综上所述我们引出了KKT条件,对于凸优化问题因为只存在唯一解KKT条件等价于原始优化问题,解KKT条件就是解原始优化问题,原始优化问题的解一定满足KKT条件。
上述就是我们所说的KKT条件,KKT条件主要用来求解,但是实际上我们发现KKT条件中的参数还是很多,求解并不容易,为此我们又引入了拉格朗日对偶性,降低要求解的维度。
2.2 参考资料
文档资料:
Qoo-凸二次规划与KTT条件-支持向量机SVM(二) - 知乎
KKT条件,原来如此简单 | 理论+算例实践 - 知乎
Karush-Kuhn-Tucker (KKT)条件 - 知乎
视频资料:
“拉格朗日对偶问题”如何直观理解?“KKT条件” “Slater条件” “凸优化”打包理解_哔哩哔哩_bilibili
拉格朗日对偶性_哔哩哔哩_bilibili
三、对偶形式
四、SMO算法
五、线性不可分情形
六、核函数
