63-哈希表

目录
1.哈希表的概念
2.哈希函数的概念
3.哈希函数的设计
3.1.key为整型时哈希函数的设计
3.1.1.普通整数
3.1.2.负整数
3.1.3.大整数
PS:哈希函数设计的3个要求:
PS:2种类型的哈希函数(大整数)
3.2.key为其他数据类型时哈希函数的设计——总的思路就是转为整型!
3.2.1.浮点数
3.2.2.字符
3.2.3.字符串
3.2.4.其他数据类型
4.哈希冲突的解决思路
4.1.闭散列/线性探测法
4.2.开散列/拉链法/链地址法
5.哈希冲突的平均查找长度
6.负载因子——描述一个哈希表的拥挤程度
7.自己实现的基于int的哈希表
7.1.向哈希表中添加一个键值对
7.2.扩容操作,默认将原哈希表长度变为2倍
7.3.删除哈希表中指定的键值对
7.4.根据key值取得对应的value
7.5.求key的hash值,最简单的对key取模即可
7.6.是否包含相应的key值
7.7.是否包含相应的value值
7.8.总代码实现
8.哈希表性能测试
9.关于JDK8的HashMap的考点说明
9.1.成员变量的说明
①static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
②static final int MAXIMUM_CAPACITY = 1 << 30;
③static final float DEFAULT_LOAD_FACTOR = 0.75f;
④static final int TREEIFY_THRESHOLD = 8;
⑤static final int UNTREEIFY_THRESHOLD = 6;
⑥static final int MIN_TREEIFY_CAPACITY = 64;
9.2.hash方法
9.3.HashMap的put方法核心逻辑
PS:put方法核心流程小结
9.4.HashMap的扩容方法
1.哈希表的概念
哈希表是查找和搜素的语义。
- 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经过关键码的多次比较。
- 顺序结构查找的时间复杂度为O(n),平衡树查找的时间复杂度即为树的高度O(log2n)。搜索的效率取决于搜索过程中元素的比较次数。
理想的搜素方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。如果构造一种存储结构,通过某种函数(hashFunc)使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。
当向该结构中:
- 插入元素:根据待插入元素的关键码,以此函数计算出该元素的存储位置,并按此位置进行存放。
- 搜素元素:对元素的关键码进行同样的计算,把求得的函数值当作元素的存储位置,在结构中按此位置取元素比较,若关键码相等,则搜素成功。
该方式即为哈希/散列方法,哈希方法中使用的转换函数称为哈希/散列函数,构造出来的结构称为哈希表(HashTable)/散列表。
数组的查找是所有数据结构中最优的时间复杂度没有之一。只要知道索引,在O(1)的时间复杂度内就能找到指定元素。
哈希表是基于数组衍生出来的数据结构,哈希表的高效性的奥秘在于数组的随机访问特性。是典型的以空间换时间的解决思路:牺牲一部分空间,最大化查找效率。
2.哈希函数的概念
将特定的“键”通过一定的函数运算得到一个整型(作为数组的索引)。
如果数字本身的值较大,可以让数组元素和下标建立一个映射关系——哈希函数。
广义的hashcode()哈希函数:将任意的数据类型变为整型值(此处将String和Student类型变为int型)
代码实现:
class Student {private String name;private int age;public Student(String name, int age) {this.name = name;this.age = age;}
}public class Test {public static void main(String[] args) {String str = "hello bit";Student student = new Student("铭哥", 18);System.out.println(str.hashCode()); //打印1195141311System.out.println(student.hashCode()); //打印356573597//hashcode()哈希函数:将任意的数据类型变为整型值(此处将String和Student类型变为int型)}
} 
3.哈希函数的设计
3.1.key为整型时哈希函数的设计
3.1.1.普通整数
数值不大时可以直接取模,让不同跨度的数据映射成一个小数据范围内的数字。模数一般用素数(数论得出的,若用合数,会有大量重复元素)。

3.1.2.负整数
将负整数的值求abs绝对值后进行哈希运算:x & 0x7fffffff 是把x进行绝对值运算。
3.1.3.大整数
像身份证号18位,直接取模的话:
- % 1000 -> 相当于取后4位
- % 1000000 -> 相当于取后6位
但这样会丢失很多身份证号中的信息,因为其他位数不参与运算。
解决:让高低位数共同参与运算(JDK中的HashMap的hash方法)。
PS:哈希函数设计的3个要求:
- 一致性:key1 = key2时,hash(key1) = hash(key2),且无论进行多少次哈希函数运算,key不变,hash值是不变的。
- 高效性:哈希函数的运算不能太耗时,尽量可以立即计算得出。小数据范围内的取模运算就是高效的。
- 均匀性:不同的key,经过hash运算后尽量避免冲突,这里的哈希冲突指key1 != key2时,hash(key1) = hash(key2)。举个极端例子:现在数值长度为10,hash()计算后的值只分布在[0, 2]这个区间内,此时就是一个不均匀的分布。
一般而言,不需要自己设计哈希函数,直接用现成的即可。
PS:2种类型的哈希函数(大整数)
①md5、md4、md3
md5主要是给String计算哈希值。Java的JDK中有现成的md5工具,但不好用。Web中用现成的第3方的md5库,直接调用.get md5()得到任意一个数据类型的md5值。
md5的3大特点:
- 定长:无论输入的数据有多长,得到的md5长度值固定(16或32位)
- 分散:如果输入的数据稍有变化,得到的md5值相差很大。(如果2个字符串str1和str2得到的md5值相同,工程上认为str1 == str2)
- 不可逆:根据任意值计算出一个md5很容易,但想根据得到的md5还原为原数据基本不可能。
md5也会发生冲突,即不同的key得到相同的md5,但这种概率在开发中基本忽略不计。
md5广泛的应用:
- 作为hash值:不能直接作为索引,一般在得到md5值之后进行再次取模得到数组索引。
- 用于加密:md5的不可逆。
- 对比文件内容:一般在下载大文件时,下载工具会默认传一个md5值,用来判断下载过程中文件是否损坏。例:源文件(10G)有固定的md5,下载后文件的md5值和源文件的md5值不同,则下载过程中文件有损坏,部分丢失。
②sha1、sha256
比md5还更加安全的哈希函数设计,位数一般为64位/128位/256位,故多用于加密、安全领域;不做为哈希值。
3.2.key为其他数据类型时哈希函数的设计——总的思路就是转为整型!
3.2.1.浮点数
计算机中就是用整数模拟小数的。
3.2.2.字符
存储的时候按照编码规则转换为整型存储。
3.2.3.字符串
按照进制转换。
166 = 1*10^2 + 6*10^1 + 6*10^0
"code" = c*26^3 + o*26^2 + d*26^1 + e*26^0
=>通用公式:任意字符串 = C*B^x(C为字符串中的字符,B为用户选的进制数,x为幂次,即当前字符C的位数)
3.2.4.其他数据类型
其他数据类型 -> String -> int
4.哈希冲突的解决思路
所谓的哈希冲突是指:不同的key经过哈希函数后得到了相同的值。(这在数学上无法避免)
若出现哈希冲突有2种常用的解决思路:①闭散列;②开散列。
4.1.闭散列/线性探测法
当发生冲突时,找冲突位置旁边有没有空闲位置。(思路简单,好放难查,更难删,工程中很少用到,知道思路即可)
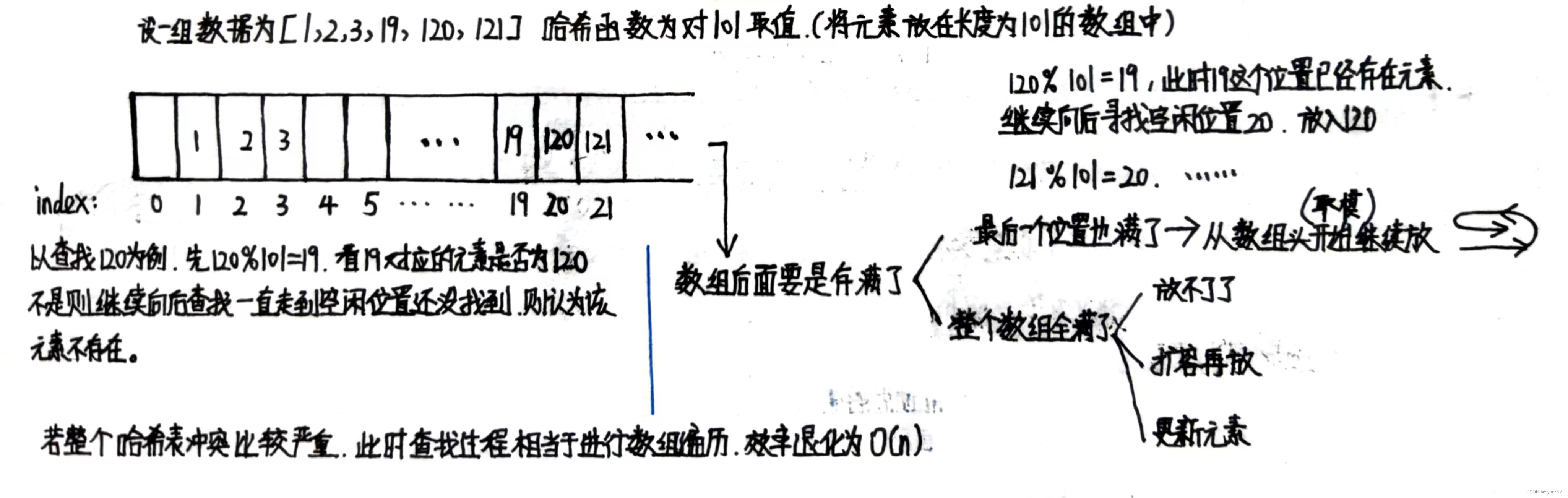
4.2.开散列/拉链法/链地址法
若出现hash冲突,就让这个位置变为一个链表或者二叉树。(简单实用,大部分工程中都采用此方法进行哈希冲突的解决,JDK的HashMap就采用链地址法解决哈希冲突)

若哈希冲突比较严重,链表的长度比较长。
解决方法:
- 扩容:将原数组扩容为更大的数组(取模double),这些链表上的节点进行再次取模,可以很大程度上避免冲突。eg.原数组长度为4,大部分元素冲突了,数组长度变为8,此时对8再次取模时,有很多冲突元素就分散在其他位置了,原来链表长度会变小。(C++的STL哈希表就是这么解决的)
- 将链表变为红黑树(JDK的HashMap在链表长度达到6个元素时,就会调整该链表为红黑树,效率从O(n) -> O(logn))/小哈希表。
根据key值求出索引值,然后根据索引再存储具体的键值对,实际上就存的是我们的node对象。
在哈希表中,key不重复,用来求索引hash();value可重复。一个key对应一个value值。
每个数组元素就是一个链表,链表头部就存储在数组中,table[0]就存储了第一个链表的头节点。
此处的插入和删除就是首先根据key求得当前要处理的链表是对应哈希表中的哪个链表。
table[hash(key)]就存储了我们要处理的链表的头节点。
5.哈希冲突的平均查找长度
例:已知一个线性表{38, 25, 74, 63, 52, 48},假定采用散列函数h(key) = key % 7(数组长度为7)(key % 7范围为0 ~ 6)计算散列地址,并散列存储在散列表A[0...5]中,若采用线性探测方法解决冲突,则在该散列表上进行等概率成功查找的平均查找长度为(2.0)。
平均查找长度 = 总的查找次数 / 总的查找的元素个数。

6.负载因子——描述一个哈希表的拥挤程度
负载因子 = 元素个数 / 数组长度
散列表的载荷因子a = 填入表中的元素个数 / 散列表的长度
a是散列表装满程度的标志因子,由于表长是定值,a与填入表中的元素个数成正比。
- 负载因子越大,表明填入表中的元素越多,产生冲突的可能性越大,效率越低。
- 负载因子越小,冲突几率小,但浪费空间。
实际上,散列表的平均查找长度是载荷因子a的函数,只是不同处理冲突的方法有不同的函数。
根据负载因子来动态判断哈希表的扩容:
当元素个数>=数组长度*负载因子,此时认为哈希表冲突比较多,可以考虑扩容(数组长度变为原来的一倍)。

对于开放定址法:负载因子是特别重要的因素,应限制在0.7-0.8以下,超过0.8,查表时的CPU缓存不命中(cache missing)按照指数曲线上升。因此一些使用开放定址法的hash库,如Java的系统库限制了载荷因子为0.75,超过此值将resize散列表。
建议以后具体项目具体对待,可以通过实验测算一下负载因子的大小,阿里要求负载因子保持在10左右(容许每个数组后链表的平均长度为10),找到时间和空间的平衡点。
7.自己实现的基于int的哈希表
7.1.向哈希表中添加一个键值对
/* 向哈希表中添加一个键值对* @param key* @param value* @return 若没有重复元素,返回value;若key已经存在,更新为新的value,返回之前的value*/
public int put(int key, int value) {//1.先求key的hash值int index = hash(key);//2.判断当前哈希表中是否已经存在了这个key,若存在,更新为value,返回旧的value//table[index]就是链表的头节点for (Node x = table[index]; x != null; x = x.next) {if(x.key == key){//此时哈希表中已经包含了key,更新为新的value,返回旧的valueint oldVal = x.val;x.val = value;return oldVal;}}//3.此时key不存在,新建一个节点头插入相应的链表中(原链表头节点——table[index])Node newNode = new Node(key, value);Node head = table[index];newNode.next = head;//更新原先头节点的指向为当前节点head = newNode;table[index] = head;size++;//4.扩容if(size >= LOAD_FACTOR * table.length) {resize();}return value;
}7.2.扩容操作,默认将原哈希表长度变为2倍
/* 扩容操作,默认将原哈希表长度变为2倍*/
private void resize() {Node[] newTable = new Node[table.length << 1];this.M = newTable.length;//遍历原哈希表for (int i = 0; i < table.length; i++) {//取出每个链表的节点,然后映射到新哈希表中//循环进行的条件,不能直接使用cur = cur.nextNode next = null;for(Node cur = table[i]; cur != null; cur = next) {//为了防止丢失下个节点的地址,第一步先使用next = cur.next;next = cur.next;int newIndex = hash(cur.key);//头插入新哈希表中cur.next = newTable[newIndex];newTable[newIndex] = cur;}}this.table = newTable;
}7.3.删除哈希表中指定的键值对
/* 删除哈希表中指定的键值对* @param key* @param value* @return*/
public boolean remove(int key, int value) {int index = hash(key);//链表的删除,判断头节点的情况if(table[index].key == key) {if(table[index].val == value) {//此时头节点就是待删除的节点Node head = table[index];table[index] = head.next;head.next = null;size--;return true;}}//头节点不是待删除的节点Node prev = table[index];while(prev.next != null) {if(prev.next.key == key) {if(prev.next.val == value) {//prev就是待删除节点的前驱prev.next = prev.next.next;size--;return true;}}prev = prev.next;}//此时就不存在这个键值对return false;
}7.4.根据key值取得对应的value
/* 根据key值取得对应的value* @param key* @return*/
public int get(int key) {//求出当前key对应的索引int index = hash(key);//遍历index对应的链表,返回key对应的valuefor (Node x = table[index]; x != null; x = x.next) {if(x.key == key) {return x.val;}}//此时key不存在return -1;
}7.5.求key的hash值,最简单的对key取模即可
/* 求key的hash值,最简单的对key取模即可* @param key* @return*/
private int hash(int key) {//先求绝对值,再取模return (key & 0x7fffffff) % this.M;
}7.6.是否包含相应的key值
7.7.是否包含相应的value值
7.8.总代码实现
/* 基于拉链法实现的哈希表* key 和 value 都存储整型*/
public class HashMapByLink {//实际存储的每个节点,冲突时使用单链表链接冲突节点private class Node{int key;int val;Node next;//有参构造方法public Node(int key, int val, Node next){this.key = key;this.val = val;this.next = next;}public Node(int key, int val) {this.key = key;this.val = val;}}//实际存储的元素个数private int size;//取模数,默认使用数组长度private int M;//默认哈希表的长度private static final int DEFAULT_CAPACITY = 16;//默认的负载因子private static final double LOAD_FACTOR = 0.75;//实际存储Node节点的数组,链表数组,每个索引后面对应的都是一个链表private Node[] table;//无参构造public HashMapByLink(){this(DEFAULT_CAPACITY);}//有参构造public HashMapByLink(int initCap){this.table = new Node[initCap];this.M = initCap;}/* 向哈希表中添加一个键值对* @param key* @param value* @return 若没有重复元素,返回value;若key已经存在,更新为新的value,返回之前的value*/public int put(int key, int value) {//1.先求key的hash值int index = hash(key);//2.判断当前哈希表中是否已经存在了这个key,若存在,更新为value,返回旧的value//table[index]就是链表的头节点for (Node x = table[index]; x != null; x = x.next) {if(x.key == key){//此时哈希表中已经包含了key,更新为新的value,返回旧的valueint oldVal = x.val;x.val = value;return oldVal;}}//3.此时key不存在,新建一个节点头插入相应的链表中(原链表头节点——table[index])Node newNode = new Node(key, value);Node head = table[index];newNode.next = head;//更新原先头节点的指向为当前节点head = newNode;table[index] = head;size++;//4.扩容if(size >= LOAD_FACTOR * table.length) {resize();}return value;}/* 扩容操作,默认将原哈希表长度变为2倍*/private void resize() {Node[] newTable = new Node[table.length << 1];this.M = newTable.length;//遍历原哈希表for (int i = 0; i < table.length; i++) {//取出每个链表的节点,然后映射到新哈希表中//循环进行的条件,不能直接使用cur = cur.nextNode next = null;for(Node cur = table[i]; cur != null; cur = next) {//为了防止丢失下个节点的地址,第一步先使用next = cur.next;next = cur.next;int newIndex = hash(cur.key);//头插入新哈希表中cur.next = newTable[newIndex];newTable[newIndex] = cur;}}this.table = newTable;}/* 删除哈希表中指定的键值对* @param key* @param value* @return*/public boolean remove(int key, int value) {int index = hash(key);//链表的删除,判断头节点的情况if(table[index].key == key) {if(table[index].val == value) {//此时头节点就是待删除的节点Node head = table[index];table[index] = head.next;head.next = null;size--;return true;}}//头节点不是待删除的节点Node prev = table[index];while(prev.next != null) {if(prev.next.key == key) {if(prev.next.val == value) {//prev就是待删除节点的前驱prev.next = prev.next.next;size--;return true;}}prev = prev.next;}//此时就不存在这个键值对return false;}/* 根据key值取得对应的value* @param key* @return*/public int get(int key) {//求出当前key对应的索引int index = hash(key);//遍历index对应的链表,返回key对应的valuefor (Node x = table[index]; x != null; x = x.next) {if(x.key == key) {return x.val;}}//此时key不存在return -1;}/* 求key的hash值,最简单的对key取模即可* @param key* @return*/private int hash(int key) {//先求绝对值,再取模return (key & 0x7fffffff) % this.M;}/* 是否包含相应的key值* @param key* @return*/public boolean containsKey(int key) {//TODO//求出当前key对应的索引int index = hash(key);//遍历index对应的链表,判断key是否存在for (Node x = table[index]; x != null; x = x.next) {if(x.key == key) {return true;}}return false;}/* 是否包含相应的value值* @param value* @return*/public boolean containsValue(int value) {//TODOreturn false;}
}8.哈希表性能测试
JDK内置的HashMap耗时<自己写到基于泛型的哈希表耗时<JDK内置的红黑树耗时。
此时可发现,在low数量级上,哈希表的性能要明显优于红黑树。
哈希表的插入、删除时间复杂度是O(1),因为默认的负载因子保证了每个链表的长度是一个比较小的常数,基本在6以内。
9.关于JDK8的HashMap的考点说明
下面从4个角度来看HashMap的源码:
- 成员变量:数据结构、树化阈值。
- 构造函数:Lazy-Load。
- put与get流程。
- 哈希算法、扩容、性能。

JDK8之前,HashMap就和我们自己写的那个基于链表的哈希表结构完全一样,但从JDK8之后,HashMap引入了红黑树,当一个链表的长度超过一个值,就会树化,将链表转为红黑树,进一步降低查找的时间复杂度,O(n)->O(logn)。
9.1.成员变量的说明
①static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;

②static final int MAXIMUM_CAPACITY = 1 << 30;
最大存储的键值对个数是2^30,当超过这个数字,单个哈希表就不能再存储了。
③static final float DEFAULT_LOAD_FACTOR = 0.75f;
默认负载因子是0.75。
④static final int TREEIFY_THRESHOLD = 8;
树化阈值。
⑤static final int UNTREEIFY_THRESHOLD = 6;
解树化:当一个红黑树不断删除元素之后,发现红黑树的元素个数<=解树化阈值6,会再次把红黑树转为链表。
⑥static final int MIN_TREEIFY_CAPACITY = 64;
树化的最小容量。
当一个链表的长度超过树化阈值8时,再判断当前整个哈希表的元素个数是否超过树化的最小容量64:若超过,将当前链表转为红黑树;若未超过,只是将哈希表扩容而不树化。
以上都是为了查找效率的最大化。
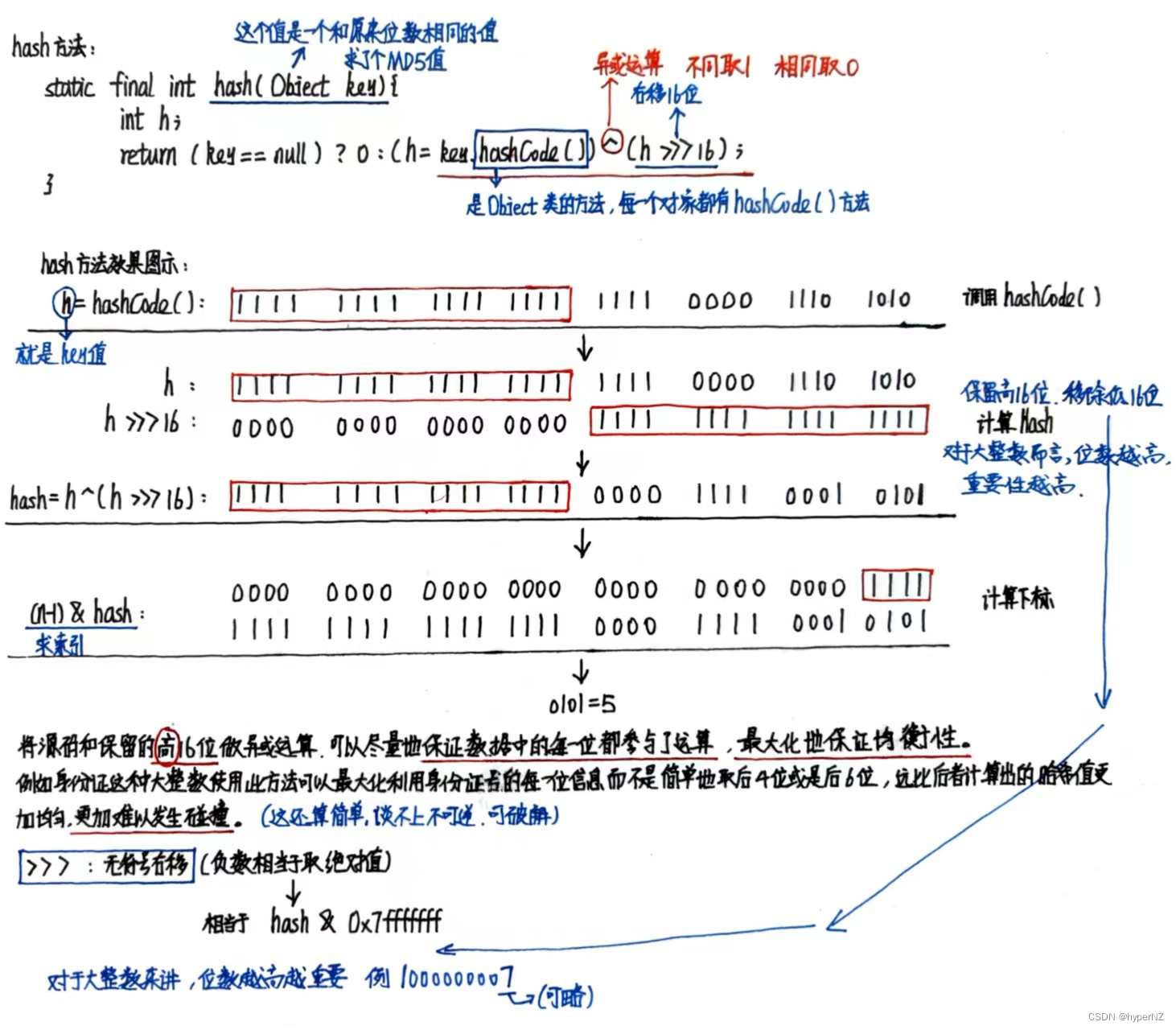
9.2.hash方法
static final int hash(Object key) {int h;return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
9.3.HashMap的put方法核心逻辑
public V put(K key, V value) {return putVal(hash(key), key, value, false, true);
}final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {Node<K,V>[] tab; Node<K,V> p; int n, i;if ((tab = table) == null || (n = tab.length) == 0) //1.此时哈希表还没初始化,调用resize进行哈希表的初始化操作。n = (tab = resize()).length;if ((p = tab[i = (n - 1) & hash]) == null) //2.当前key对应的哈希表中链表为空,创建一个新节点将key和value放入,此节点就是当前链表的头节点。tab[i] = newNode(hash, key, value, null);else { //3.此时哈希表非空且头节点不为空Node<K,V> e; K k;if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) //3.1.p是链表的头节点,链表的头节点的key恰好等于要存储的keye = p; //临时变量赋值else if (p instanceof TreeNode) //3.2.此时链表的头节点不为空,且头节点的key不等于传入的key,此时节点已经树化,调用红黑树的插入方法,将当前键值对按照红黑树节点插入e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);else { //3.3.当前链表头部不为空,且key不是当前key,调用链表的插入方法插入一个新链表节点for (int binCount = 0; ; ++binCount) {if ((e = p.next) == null) {p.next = newNode(hash, key, value, null);if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st //当链表个数>=7时,尝试树化操作treeifyBin(tab, hash);break;}if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))break;p = e;}}if (e != null) { // existing mapping for keyV oldValue = e.value;if (!onlyIfAbsent || oldValue == null)e.value = value;afterNodeAccess(e);return oldValue;}}++modCount;if (++size > threshold) //扩容resize();afterNodeInsertion(evict);return null;
}PS:put方法核心流程小结
- 若HashMap还未初始化,先进行哈希表的初始化操作(默认初始化为16个桶)。
- 对传入的key值做hash,得出要存放该元素的桶编号。
- 若没有发生碰撞,即头节点为空,将该节点直接存放到桶中作为头节点。
- 若发生碰撞:a.此时桶中的链表已经树化,将节点构造为树节点后加入红黑树。b.链表还未树化,将节点作为链表的最后一个节点入链表。
- 若哈希表中存在key值相同的元素,替换最新的value值。
- 若桶满了(size++大于threshold),调用resize()扩容哈希表。threshold = 容量(默认16)* 负载因子(默认0.75)。
9.4.HashMap的扩容方法
final Node<K,V>[] resize() {Node<K,V>[] oldTab = table;int oldCap = (oldTab == null) ? 0 : oldTab.length;int oldThr = threshold;int newCap, newThr = 0;if (oldCap > 0) {if (oldCap >= MAXIMUM_CAPACITY) {threshold = Integer.MAX_VALUE;return oldTab;}else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) //扩容为原来的一倍newThr = oldThr << 1; // double threshold}else if (oldThr > 0) // initial capacity was placed in thresholdnewCap = oldThr;else { // zero initial threshold signifies using defaultsnewCap = DEFAULT_INITIAL_CAPACITY;newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);}if (newThr == 0) {float ft = (float)newCap * loadFactor;newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?(int)ft : Integer.MAX_VALUE);}threshold = newThr;@SuppressWarnings({"rawtypes","unchecked"})Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];table = newTab;if (oldTab != null) {for (int j = 0; j < oldCap; ++j) {Node<K,V> e;if ((e = oldTab[j]) != null) {oldTab[j] = null;if (e.next == null)newTab[e.hash & (newCap - 1)] = e;else if (e instanceof TreeNode)((TreeNode<K,V>)e).split(this, newTab, j, oldCap);else { // preserve orderNode<K,V> loHead = null, loTail = null;Node<K,V> hiHead = null, hiTail = null;Node<K,V> next;do {next = e.next;if ((e.hash & oldCap) == 0) {if (loTail == null)loHead = e;elseloTail.next = e;loTail = e;}else {if (hiTail == null)hiHead = e;elsehiTail.next = e;hiTail = e;}} while ((e = next) != null);if (loTail != null) {loTail.next = null;newTab[j] = loHead;}if (hiTail != null) {hiTail.next = null;newTab[j + oldCap] = hiHead;}}}}}return newTab;
}




