讨论：股市交易中的策略与挑战

# 引言

在金融市场中，股票交易是一种常见的投资方式。股票交易不仅涉及到资金的投入，还涉及到策略的选择，这包括选择购买和出售股票的时机，以及考虑可能的交易成本。这两种情况下，算法都扮演了重要角色。本文将探讨股市交易中的一些算法策略，特别是买卖股票的最佳时机以及含冷冻期的交易策略，并提供相关的代码示例。

# 相关问题：

1. 最佳买卖股票时机：如何有效地选择买入和卖出的最佳时机，以最大化收益？

2. 股票交易中的冷冻期：在某些策略中，投资者可能会选择在一段时间内不进行任何交易，这被称为冷冻期。如何将冷冻期整合进交易策略中？

# 相关答案：

1. 最佳买卖股票时机的算法：

- 算法一：对于常规的股票交易，可以使用动态规划来解决。例如，通过动态规划计算在给定条件下，获得的最大收益。这种算法可以处理包含多个交易日的股票市场，通过计算每个交易日可能的最大收益来决定何时买入和卖出。
- 算法二：另一种策略是使用基于市场趋势的算法，如移动平均线交叉策略。这种策略通过观察短期和长期移动平均线的交叉来决定买卖时机。

示例代码（使用动态规划）：
`cpp
// 示例：使用动态规划计算最大收益
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
if (n <= 1) return 0; int dp0 = -prices[0], dp1 = 0; for (int i = 1; i < n; ++i) { int newDp0 = max(dp0, dp1 + prices[i]); int newDp1 = max(dp1, dp0 - prices[i]); dp0 = newDp0; dp1 = newDp1; } return dp1 >= 0 ? dp1 : dp0;
}
};
`

2. 股票交易中的冷冻期：

- 处理冷冻期的策略包括在交易策略中设置明确的规则，比如在一定时间不进行任何交易，或者限制每天的交易次数。这可以通过简单的逻辑设计实现，或者利用复杂算法如马尔可夫决策过程来进行动态调整。

示例策略：
`plaintext
1. 决定冷冻期长度（如一周或一个月）
2. 在每个交易日检查是否到达冷冻期结束
3. 如果没有，执行买入或卖出操作
4. 到达冷冻期后，开始下一个交易周期
`

# 结论

通过上述讨论，我们可以看到，无论是通过简单的动态规划还是复杂的机器学习算法，股市交易中的策略都是多样的，可以根据不同的市场条件和个人偏好来选择。这些策略不仅涉及金融知识，还涉及到数据分析和算法应用，是现代投资的基石之一。

309. 最佳买卖股票时机含冷冻期

动规五部曲

1、确定dp数组以及下标的含义

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

具体可以区分出如下四个状态：

• 状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
• 不持有股票状态，这里就有两种卖出股票状态
  • 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
  • 状态三：今天卖出股票
• 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天！

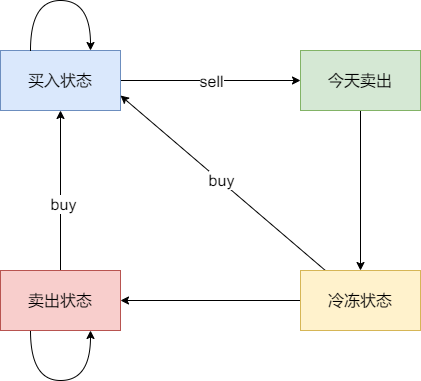
j的状态为：

• 0：状态一
• 1：状态二
• 2：状态三
• 3：状态四

注意这里的每一个状态，例如状态一，是持有股票股票状态并不是说今天一定就买入股票，而是说保持买入股票的状态即：可能是前几天买入的，之后一直没操作，所以保持买入股票的状态。 

2、确定递推公式

达到买入股票状态（状态一）即：dp[i][0]，有两个具体操作：

• 操作一：前一天就是持有股票状态（状态一），dp[i][0] = dp[i - 1][0]
• 操作二：今天买入了，有两种情况
  • 前一天是冷冻期（状态四），dp[i - 1][3] - prices[i]
  • 前一天是保持卖出股票的状态（状态二），dp[i - 1][1] - prices[i]

那么dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);

达到保持卖出股票状态（状态二）即：dp[i][1]，有两个具体操作：

• 操作一：前一天就是状态二
• 操作二：前一天是冷冻期（状态四）

dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);

达到今天就卖出股票状态（状态三），即：dp[i][2] ，只有一个操作：

昨天一定是持有股票状态（状态一），今天卖出

即：dp[i][2] = dp[i - 1][0] + prices[i];

达到冷冻期状态（状态四），即：dp[i][3]，只有一个操作：

昨天卖出了股票（状态三）

dp[i][3] = dp[i - 1][2];

3、dp数组如何初始化

如果是持有股票状态（状态一）那么：dp[0][0] = -prices[0]，一定是当天买入股票。

保持卖出股票状态（状态二），只能初始为0

今天卖出了股票（状态三），同上分析，dp[0][2]初始化为0，dp[0][3]也初始为0。

4、确定遍历顺序

从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

5、举例推导dp数组

以 [1,2,3,0,2] 为例，dp数组如下：

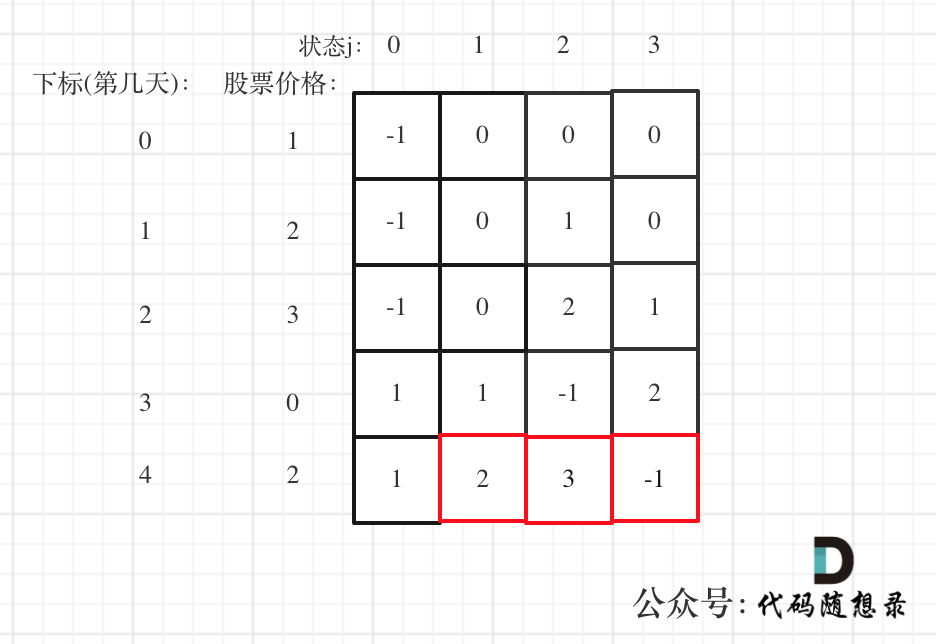
最后结果是取 状态二，状态三，和状态四的最大值

状态四是冷冻期，最后一天如果是冷冻期也可能是最大值。 

class Solution {
public:int maxProfit(vector<int>& prices) {if (prices.size() == 0) return 0;int len = prices.size();vector<vector<int>> dp(len, vector<int>(4,0));dp[0][0] = -prices[0];for (int i = 1; i < len; i++) {dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i],dp[i - 1][1] - prices[i]));dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);dp[i][2] = dp[i - 1][0] + prices[i];dp[i][3] = dp[i - 1][2];}return max(dp[len - 1][1], max(dp[len - 1][2], dp[len - 1][3]));}
};

714. 买卖股票的最佳时机含手续费

与普通买卖股票问题一致，手续费可以放在买入股票时，也可以放在卖出股票时进行计算

本题把手续费算入买入股票时

动规五部曲：

1、确定dp数组以及下标的含义

dp[i][j]，第i天状态为j，所剩的最多现金为dp[i][j]。

可以分为两种状态：状态一：不持有股票（j为0）；状态二：持有股票（j为1）

2、确定递推公式

不持有股票状态：有两种情况

• 昨天不持有
• 昨天持有，今天把昨天股票卖出

dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]

持有股票状态：

• 昨天已持有
• 昨天未持有，今天买入股票

dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee)

3、dp数组如何初始化

不持有股票 dp[0][0] = 0;

持有股票 dp[0][1] = -prices[0] - fee;

4、确定遍历顺序

从递归公式上可以看出，dp[i] 依赖于 dp[i-1]，所以是从前向后遍历。

5、举例推导dp数组

以 prices = [1, 3, 2, 8, 4, 9], fee = 2 为例

class Solution {
public:int maxProfit(vector<int>& prices, int fee) {if (prices.size() == 0) return 0;vector<vector<int>> dp(prices.size(), vector<int>(2,0));dp[0][0] = 0;dp[0][1] = -prices[0] - fee;for (int i = 1; i < prices.size(); i++) {dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i] - fee);}return max(dp[prices.size() - 1][0], dp[prices.size() - 1][1]);}
};