算法 二叉树2 || 层序遍历 226.翻转二叉树 101. 对称二叉树 104.二叉树的最大深度 111 二叉树的最小深度 222.完全二叉树的节点个数

102 二叉树的层序遍历

队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

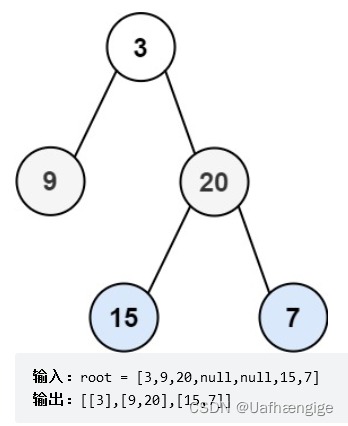
迭代法：

/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> res;queue<TreeNode*> que;if(root == nullptr) return {};que.push(root);while(!que.empty()){int size = que.size();vector<int> vec;for(int i = 0; i < size; ++i){TreeNode* cur = que.front();que.pop();vec.push_back(cur->val);if(cur->left)  que.push(cur->left);if(cur->right) que.push(cur->right);}res.push_back(vec);}return res;}
};

递归法：
递归在遍历的时候，会一层层下去，不能像队列一样遍历一层处理一层。所以递归法层序遍历可以使用变量depth来协助指明当前元素的深度。因为存放元素的容器是二维数组，横向的顺序可以根据左右元素的处理顺序决定，纵向则可以使用depth来控制
其中注意这一行：
if (result.size() == depth) result.push_back(vector());
递归一路向左遍历，遇到每一行的最左边的第一个值才重新创建一行。

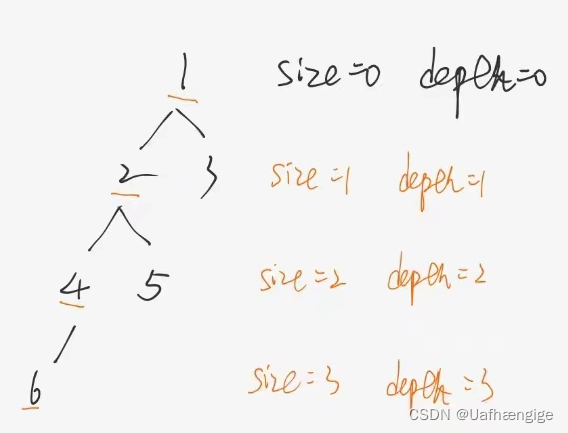
class Solution {
public:void order(TreeNode* cur, vector<vector<int>>& result, int depth){if (cur == nullptr) return;if (result.size() == depth) result.push_back(vector<int>());result[depth].push_back(cur->val);order(cur->left, result, depth + 1);order(cur->right, result, depth + 1);}vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> result;int depth = 0;order(root, result, depth);return result;}
};

107.二叉树的层次遍历 II

很简单，把102的res 反转一下就行

class Solution {
public:vector<vector<int>> levelOrderBottom(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(vec);}reverse(result.begin(), result.end()); // 在这里反转一下数组即可return result;}
};

199.二叉树的右视图

注意题意：是右视图，而不是只看最右侧的节点。所以下面这个二叉树返回的应该是1 3 4而不是 1 3。在遍历的时候依旧要遍历左子树，只是返回每一层最右侧的值即可。

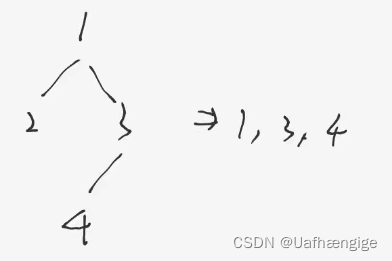
/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> rightSideView(TreeNode* root) {if(root == nullptr) return {};vector<int> res;queue<TreeNode*> que;que.push(root);while(!que.empty()){int size = que.size();for(int i = 0; i<size; i++){TreeNode* cur = que.front();que.pop();if(i == size-1) res.push_back(cur->val);if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);} }return res;}
};

637.二叉树的层平均值

class Solution {
public:vector<double> averageOfLevels(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<double> result;while (!que.empty()) {int size = que.size();double sum = 0; // 统计每一层的和for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();sum += node->val;if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(sum / size); // 将每一层均值放进结果集}return result;}
};

429.N叉树的层序遍历

别被什么用null分割给唬住，看node 的结构，以前是两根左右指针，现在是一个vector<Node*>容器而已

class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size();vector<int> vec;for (int i = 0; i < size; i++) {Node* node = que.front();que.pop();vec.push_back(node->val);for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列if (node->children[i]) que.push(node->children[i]);}}result.push_back(vec);}return result;}
};

515.在每个树行中找最大值

class Solution {
public:vector<int> largestValues(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<int> result;while (!que.empty()) {int size = que.size();int maxValue = INT_MIN; // 取每一层的最大值for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();maxValue = node->val > maxValue ? node->val : maxValue;if (node->left) que.push(node->left);if (node->right) que.push(node->right);}result.push_back(maxValue); // 把最大值放进数组}return result;}
};

116.填充每个节点的下一个右侧节点指针

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if (root == nullptr) return root;queue<Node*> que;if(root->left) que.push(root->left);if(root->right) que.push(root->right);while(!que.empty()){int size = que.size();for(int i = 1; i < size; ++i){Node* cur1 = que.front(); //左que.pop();Node* cur2 = que.front(); //右cur1->next = cur2;if(cur1->left) que.push(cur1->left);if(cur1->right) que.push(cur1->right);if(i == size-1){que.pop();if(cur2->left) que.push(cur2->left);if(cur2->right) que.push(cur2->right);} }}return root;}
};

117.填充每个节点的下一个右侧节点指针II

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {if(root == NULL) return root;queue<Node*> que;que.push(root);while(!que.empty()){int size = que.size();Node* pre;Node* cur;for(int i = 0; i < size; ++i){if(i == 0){pre = que.front();que.pop();cur = pre;}else{cur = que.front();que.pop();pre->next = cur;pre = cur;}if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}}return root;}
};

104.二叉树的最大深度

/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr) return 0;int depth = 0;queue<TreeNode*> que;que.push(root);while(!que.empty()){int size = que.size();for(int i = 0; i < size; ++i){TreeNode* cur = que.front();que.pop();if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}depth++;}return depth;}
};

111.二叉树的最小深度

/* Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(root == nullptr) return 0;int depth = 0;queue<TreeNode*> que;que.push(root);while(!que.empty()){int size = que.size();depth++;for(int i = 0; i < size; ++i){TreeNode* cur = que.front();que.pop();if(cur->left == nullptr && cur->right == nullptr) return depth;if(cur->left) que.push(cur->left);if(cur->right) que.push(cur->right);}}return depth;}
};

226.翻转二叉树

递归的时候除了中序都可以（中序会让部分节点反转两次）
递归法：

class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;swap(root->left, root->right);  // 中invertTree(root->left);         // 左invertTree(root->right);        // 右return root;}
};

深度迭代法（stack）

class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (root == NULL) return root;stack<TreeNode*> st;st.push(root);while(!st.empty()) {TreeNode* node = st.top();              // 中st.pop();swap(node->left, node->right);if(node->right) st.push(node->right);   // 右if(node->left) st.push(node->left);     // 左}return root;}
};

101. 对称二叉树

思路：
1、递归
本题遍历只能是“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。
在终止条件中，首先看两个中节点是不是相同，如果中节点都不相同就没必要往下看，然后才是他们对应子树，只有子树相同，中节点这里才能返回true。

class Solution {
public:bool isSymmetric(TreeNode* root) {if (root == NULL) return true;return compare(root->left,root->right);}bool compare(TreeNode* left, TreeNode* right){if(left == nullptr && right != nullptr) return false;else if(left != nullptr && right == nullptr) return false;else if(left == nullptr && right == nullptr) return true;else if(left->val != right->val) return false;bool isleft = compare(left->left,right->right);bool isright = compare(left->right, right->left);return isleft && isright;}
};

2、层序遍历，放进队列中，两两取出比较即可

class Solution {
public:bool isSymmetric(TreeNode* root) {if(root == nullptr) return true;queue<TreeNode*> que;que.push(root->left);que.push(root->right);while(!que.empty()){TreeNode* left = que.front(); que.pop();TreeNode* right = que.front(); que.pop();if(left == nullptr && right != nullptr) return false;else if(left != nullptr && right == nullptr) return false;else if(left == nullptr && right == nullptr) continue;else if(left->val != right->val) return false;que.push(left->left); que.push(right->right);que.push(left->right); que.push(right->left);}return true;}
};

3、深度遍历，使用栈
把队列直接换成栈就可以

104.二叉树的最大深度

在层序遍历中，使用的队列。现在使用递归法。
本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度： 指从该节点到叶子节点的最长简单路径边的条数后者节点数（取决于高度从0开始还是从1开始）

1、而根节点的高度就是二叉树的最大深度，所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

class Solution {
public:int maxDepth(TreeNode* root) {return maxdepth(root);}int maxdepth(TreeNode* cur){if(cur == nullptr) return 0;int depth ;int leftdepth = maxdepth(cur->left);int rightdepth = maxdepth(cur->right);depth = max(leftdepth,rightdepth);return depth+1; //depth记录的是当前中节点左右两节点的高度。返回的时候要加上中节点自身的高度，所以返回depth+1}
};

2、真正求深度的逻辑 前序遍历

class Solution {
public:int result;int maxDepth(TreeNode* root) {if(root == nullptr) return 0;result = 0;maxdepth(root,1);return result;}void maxdepth(TreeNode* cur,int depth){result = depth > result ? depth : result;if(cur->left == nullptr && cur->right == nullptr) return;if(cur->left){depth++;maxdepth(cur->left,depth);depth--;}if(cur->right){depth++;maxdepth(cur->right,depth);depth--;}}
};

111 二叉树的最小深度

前序遍历：

class Solution {
private:int result;void getdepth(TreeNode* node, int depth) {if (node->left == NULL && node->right == NULL) {result = min(depth, result);  return;}// 中 只不过中没有处理的逻辑if (node->left) { // 左getdepth(node->left, depth + 1);}if (node->right) { // 右getdepth(node->right, depth + 1);}return ;}public:int minDepth(TreeNode* root) {if (root == NULL) return 0;result = INT_MAX;getdepth(root, 1);return result;}
};

后序遍历（很不熟）

class Solution {
public:int getDepth(TreeNode* node) {if (node == NULL) return 0;int leftDepth = getDepth(node->left);           // 左int rightDepth = getDepth(node->right);         // 右// 中// 当一个左子树为空，右不为空，这时并不是最低点if (node->left == NULL && node->right != NULL) { return 1 + rightDepth;}   // 当一个右子树为空，左不为空，这时并不是最低点if (node->left != NULL && node->right == NULL) { return 1 + leftDepth;}int result = 1 + min(leftDepth, rightDepth);return result;}int minDepth(TreeNode* root) {return getDepth(root);}
};

222.完全二叉树的节点个数

class Solution {
public:int countNodes(TreeNode* root) {int leftcount = 0;int rightcount = 0;if(root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;while(left){leftcount++;left = left->left;}while(right){rightcount++;right = right->right;}if(leftcount == rightcount){return (2<<leftcount) - 1;}return countNodes(root->left) + countNodes(root->right) + 1;}
};