大数乘法【极简思路、代码模板】

793. 高精度乘法 - AcWing题库
极简思路
大数乘法可能和前面我们提到的大数减法 和 大数加法 的分治 思路不太一样,对于大数乘法我们可以有更加简单的思路。
这里提到的大数乘法,是针对与
一个很大的数 * 一个正常的整数
而不是两个超大整数相乘
所以这里我们其实可以简化的是——只需要将大数中的每一位都与正常整数相乘,然后再将每一位放入vector后输出即可
问题一:为什么可以这么计算?
首先我们可以用一种抽象的眼光观看乘法的计算过程
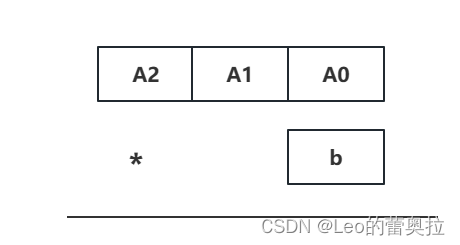
当前我们有一个数A2A1A0 和 小b相乘,我们首先观察个位
一定是由
A0 * b % 10得到的结果而十位 则是有
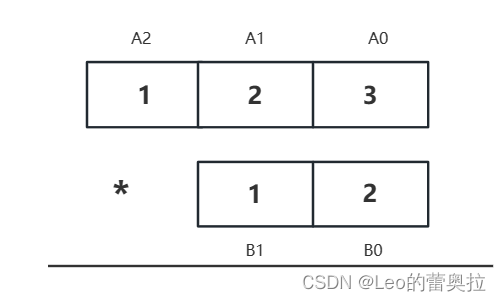
A0 * b / 10 + A1 * b % 10得到的现在我们针对一个实例123 * 12 进行讲解
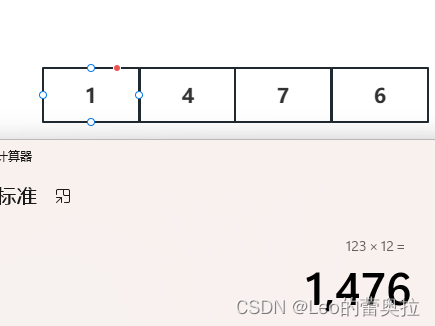
同样的,我们将每一位拆开
最后得到结果
代码模板
#include<iostream>
#include<vector>using namespace std;vector<int> muli(vector<int> &A , int b){vector<int> C;int t = 0 ;for(int i = 0 ; i < A.size() || t != 0 ; i ++){if(i < A.size()) t += A[i] * b;C.push_back(t % 10);t /= 10;}// 去除前导0while(C.size() > 1 && C.back() == 0) C.pop_back();return C;}int main(){vector<int> A;string a ;int b ;cin >> a >> b;for(int i = a.size() - 1 ; i >= 0 ; i --) A.push_back(a[i] - '0');vector<int> C = muli(A , b);for(int i = C.size() - 1 ; i >= 0 ; i --) cout << C[i];return 0;
}
问题二:这个循环条件里面为什么会有t != 0?
因为根据我们上面对乘法的分析,t 就是我们这里的前一位的进位
所以一定要确保没有进位(防止出现最后一位
最高位丢失的情况)