带头双向循环链表的结构

带头双向循环链表的结构如下图：

可以看到，带头双向循环链表是结构最复杂的链表

但是在实际使用链表结构存储数据时，都是使用带头双向循环链表，虽然这个结构有些复杂，但是这样的结构会给我们带来很多优势，实现代码的时候反而简单了

下面我们来实现一下带头双向循环链表

带头双向循环链表的实现

因为这是一个双向链表，所以要在结构体中定义2个结构体类型指针，用来指向节点的前一个结点和后一个结点

所以带头双向循环链表的结构体如下：

typedef int LTDataType;typedef struct ListNode
{struct ListNode* prev;struct ListNode* next;LTDataType data;}LTNode;

建立新节点

这里还是使用malloc去建立一个结点，其余的与单链表中建立新节点类似，这里不多说。

LTNode* BuyNewNode(LTDataType x)
{LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;return newnode;
}

初始化函数

因为这个结构是包含头节点的，所以要在初始化函数中把头节点定义出来

LTNode* phead = BuyNewNode(-1);

因为此时只有头节点一个结点，又因为结构是循环的，所以头节点的下一个结点和上一个节点都是头节点自己

phead->next = phead;
phead->prev = phead;

所以，初始化的代码为：

LTNode* LTInit()
{LTNode* phead = BuyNewNode(-1);phead->next = phead;phead->prev = phead;return phead;
}

打印函数

void LTPrint(LTNode* phead)
{assert(phead);LTNode* cur = phead->next;printf("<=>head<=>");while (cur!= phead){printf("%d<=>", cur->data);cur = cur->next;}printf("\\n");
}

判空函数

当只剩头节点一个节点时，链表就为空了，所以当phead->next == phead时，就说明链表为空了

bool LTEmpty(LTNode* phead)
{assert(phead);return phead->next == phead;
}

尾插函数

尾插函数第一步就是要找尾，在单链表中，想要找到尾就需要遍历一遍链表，效率低耗时

但是在带头双向循环链表中，找到尾很简单，尾节点就是头节点的前一个节点

然后再依次将结点前后链接上即可

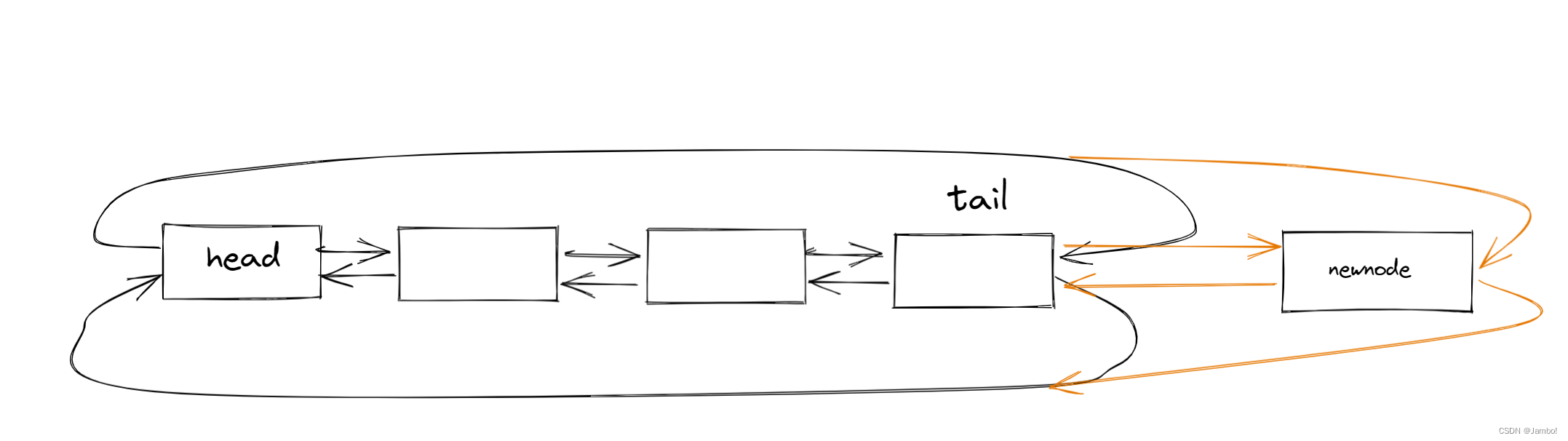
void LTPushBack(LTNode* phead, LTDataType x)
{assert(phead);LTNode* newnode = BuyNewNode(x);LTNode* tail = phead->prev;tail->next = newnode;newnode->prev = tail;newnode->next = phead;phead->prev = newnode;
}

头插函数

在实现单链表时，头节点就是头指针指向的结点
在带头双向循环链表中，头节点就是头节点的下一个结点

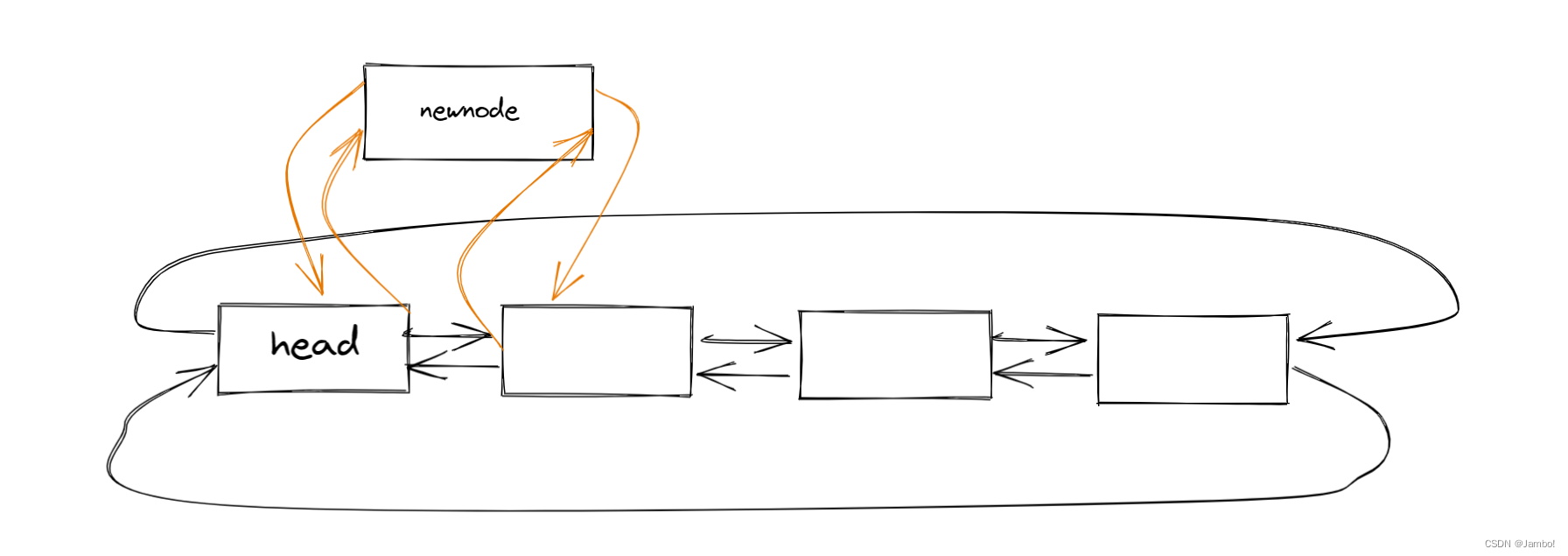
void LTPushFront(LTNode* phead, LTDataType x)
{assert(phead);LTNode* newnode = BuyNewNode(x);LTNode* nex = phead->next;phead->next = newnode;newnode->prev = phead;newnode->next = nex;nex->prev = newnode;
}

尾删函数

在单链表中，我们循环需要找到尾节点以及尾节点前面的节点，十分的麻烦
但是在带头双向循环链表中，就没有这样的问题

头节点的prev就是尾节点tail，尾节点的prev就是尾节点的前一个节点tailprev

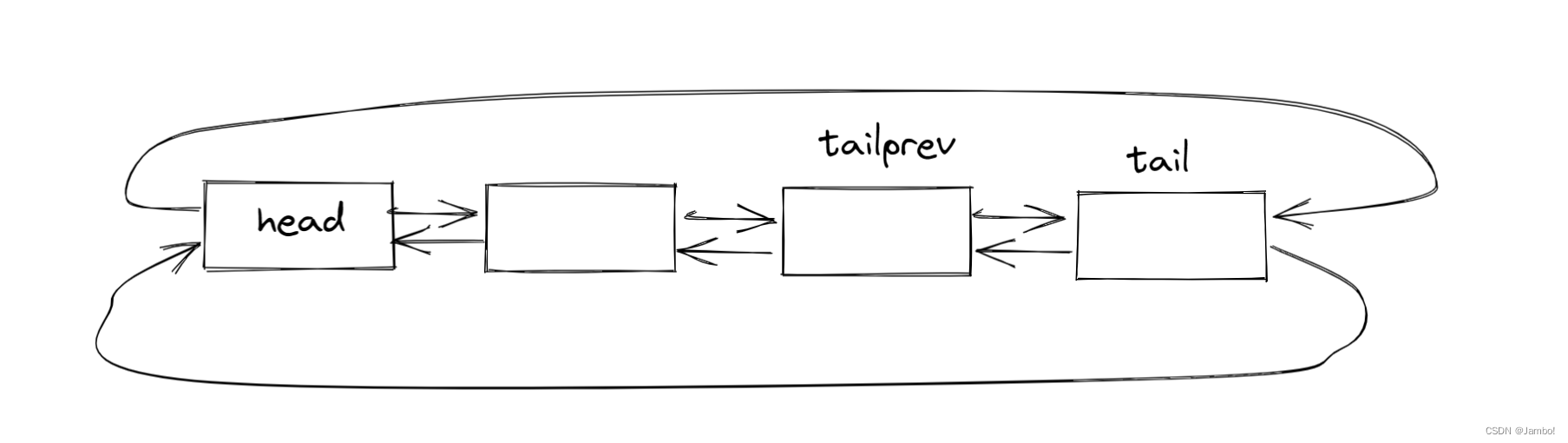
然后将tailprev当成尾节点链接起来，最后free掉tail

void LTPopBack(LTNode* phead)
{assert(phead);assert(!LTEmpty(phead));LTNode* tail = phead->prev;LTNode* tailprev = tail->prev;tailprev->next = phead;phead->prev = tailprev;free(tail);tail = NULL;
}

头删函数

void LTPopFront(LTNode* phead)
{assert(phead);assert(!LTEmpty(phead));LTNode* del = phead->next;LTNode* nex = del->next;phead->next = nex;nex->prev = phead;free(del);del = NULL;
}

头删与尾删类似，不多说

查找函数

在单链表中，查找某个节点的循环条件是什么时候遇到空，什么时候结束循环

在带头双向循环链表中，循环条件则是遇到头节点，就结束循环

LTNode* LTFind(LTNode* phead,LTDataType x)
{assert(phead);LTNode* cur = phead->next;while (cur != phead){if (cur->data == x){return cur;}cur = cur->next;}return NULL;
}

插入函数

在pos位置前插入，这个pos的地址是由LTFind函数返回的

如果我们直接就将新的节点newnode插入到pos前面位置，它们之间的链接操作有一定的顺序，如果随意改变链接关系是会出问题的

所以我们可以用一个指针posprev去保存pos->prev的地址，然后再链接posprev、newnode和 pos间的链接关系，这时的链接关系的改变不需要按照一定的顺序，按照逻辑随意修改

void LTInsert(LTNode* pos, LTDataType x)
{assert(pos);LTNode* posprev = pos->prev;LTNode* newnode = BuyNewNode(x);posprev->next = newnode;newnode->prev = posprev;newnode->next = pos;pos->prev = newnode;}

我们可以用这个删除函数与实现头插和尾插

尾插：因为在pos前插入，头节点的前一个结点就是尾结点，所以调用LTInsert函数时传的地址是phead

void LTPushBack(LTNode* phead, LTDataType x)
{assert(phead);LTInsert(phead, x); //调用LTInsert函数尾插
}

头插：phead->next的前插入就是头插，所以传参为phead->next

void LTPushFront(LTNode* phead, LTDataType x)
{assert(phead);LTInsert(phead->next, x); //调用LTInsert函数头插
}

删除函数

这里的操作也如上个函数一样，用一个指针posprev保存pos->prev的地址，用指针posnext保存pos->next的地址，然后链接posprev和posnext

随后free掉pos即可

void LTErase(LTNode* pos)
{assert(pos);LTNode* posprev = pos->prev;LTNode* posnext = pos->next;posprev->next = posnext;posnext->prev = posprev;free(pos);pos = NULL;
}

这个函数还有个瑕疵就是：
如果pos传的是哨兵位头节点的地址，那么删除操作就会出错
这里如果想检查，就需要传一个参数，用来比较pos和头节点地址是否相同，但是没有必要
在后面C++中会有更好的写法

同样，可以调用LTErase去实现头删和尾删

头删：

void LTPopFront(LTNode* phead)
{assert(phead);assert(!LTEmpty(phead));LTErase(phead->next);}

尾删：

void LTPopBack(LTNode* phead)
{assert(phead);assert(!LTEmpty(phead));LTErase(phead->prev);
}

销毁函数

void LTDestroy(LTNode* phead)
{assert(phead);LTNode* del = phead->next;LTNode* nex = del->next;while (del!= phead){free(del);del = nex;nex = nex->next;}free(phead);phead = NULL;
}

带头双向循环链表的特点

在前面实现的过程中可以发现：

• 以往单链表的尾删、删除和插入操作的时间复杂度是 O(n),因为需要找尾或找前一个结点，但是带头双向循环链表完美得解决了这个问题，我们可以通过phead->prev找到尾，通过某一结点的prev找到前一个结点，所以在带头双向循环链表中，尾删和插入的时间复杂度为O(1)
• 在单链表的头插、尾插、头删、尾删等函数中，传的参数有二级指针，不容易理解，但是带头双向循环链表有头节点，传参是头节点的地址，因为在函数中是不会改变这个地址的指向，所以不用传二级指针

链表和顺序表的对比

这两个结构各有优势，很难说谁更优，这两个结构相辅相成

顺序表：

• 物理上存储空间连续
• 支持随机访问
• 任意位置插入或者删除元素可能需要搬移元素，效率低O(N)
• 连续物理空间，空间不够后需要增容。增容有一定程度的消耗

链表：

• 物理上存储空间不连续，但是逻辑上连续
• 不支持随机访问
• 任意位置插入删除效率高
• 按需申请释放空间