C-- V1.0

E -> n

   |   true

   |   false

   |   E + E

   |   E && E

类型合法的程序：

• 3 + 4
• false && true

类型不合法的程序：

• 3 + true
• true + false 

对这个语言，语义分析的任务是：对给定的一个表达式e，写一个函数type check(e);返回表达式e的类型；若类型不合法，则报错。

针对C -- 语言构造的类型检查伪代码算法如下：

（ps：其中的数据结构定义可参考抽象语法树的定义（C语言版）_青衫客36的博客-CSDN博客）

enum type {INT, BOOL};enum type check_exp(Exp_t e)
{switch (e->kind){case EXP_INT:   return INT;case EXP_TRUE:  return BOOL;case EXP_FALSE: return BOOL;case EXP_ADD:   t1 = check_exp(e->left);t2 = check_exp(e->right);if (t1 != INT || t2 != INT)error("type mismatch");else return INT;case EXP_AND:   t1 = check_exp(e->left);t2 = check_exp(e->right);if (t1 != BOOL || t2 != BOOL)error("type mismatch");else return BOOL;default:break;}
}

C-- V2.0

接下来我们把这个语言稍微扩展一下，我们加上变量声明，看看对变量声明该如何处理。

P ->  D E

D -> T id; D

   |

T ->  int

   |    bool

E -> n

   |    id

   |    true

   |    false

   |    E + E

   |    E && E

注：P为程序，D为变量声明，E为表达式，T为数据类型，上述产生式中的id为变量，n为常数

类型合法的程序1：

int x;

x + 4

x的类型在第一行声明，需要做一个向上引用，体现了上下文相关分析的意思。 

类型合法的程序2：

bool y;

false && y

类型不合法的程序1：

x + 3

变量在使用之前没有声明。

类型不合法的程序2：

int x;

x + false

x是整形，整形+布尔类型是不合法的。 

此时的类型检查算法变更如下：

enum type {INT, BOOL};
Table_t table;  // 符号表// 检查程序
enum type check_prog(Dec_t d, Exp_t e)
{// 递归的对声明部分做检查，检查完之后给table赋值，初始化全局符号表table = check_dec(d);return check_exp(e); // 整个程序类型为内部表达式类型
}// 检查变量声明
Table_t check_dec(Dec_t d)
{foreach(T id ∈ d)table_enter(table, id, T) // 将每个变量名、变量类型插入符号表
}// 检查表达式
enum type check_exp(Exp_t e)
{switch (e->kind){case EXP_ID:t = Table_lookup(table, id);if (id not exist)error("id not found");else return t;}
}

此处的符号表可以理解为key -> value 的映射 [ id -> type ]

假设给定如下C--程序:

int x;
bool y;
4 + x;

其对应的语法树如下： 

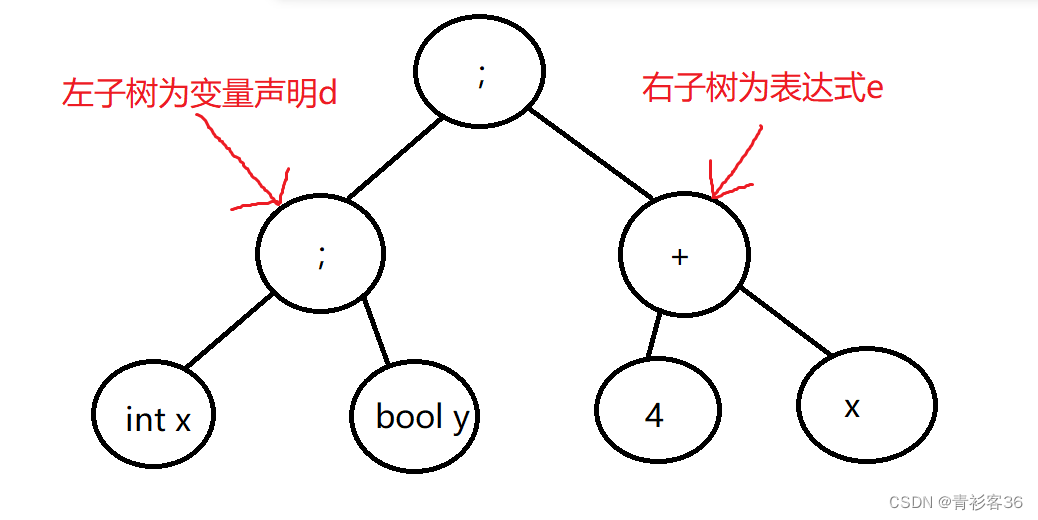
首先程序先来检查左子树（变量声明d的部分），对其中的每一个变量声明去填符号表，做完第一部分，这个table就生成好了，符号表如下所示。

然后有了这个全局变量table，我们根据这个符号表继续来看check_exp(e)（即接下来对表达式的类型检查是怎么做的）

对于表达式中的变量x，我们先做一个表的查找操作，如果id在这个表里面没有查到的话，直接报错，此时对应这种情况，即有一个变量正在使用，但是这个变量没有声明过。否则，说明变量x存在，那么一定会找到类型t，然后把t返回回去即可。（ps：具体可见上面的代码）

总结一下，这个类型检查算法其实也是另外一种后序遍历，首先对于整个程序来说，先遍历其左子树（所有的声明部分），这个声明部分构造一张全局的表，然后在递归调用右子树的时候，变量可以根据这个表进行查找，可以帮助右边表达式做类型检查。

所谓上下文相关检查，核心的概念就是这张符号表，即把上下文相关的信息存储到这里面，接下来用的时候再去表里面来查。

C-- V3.0

接下来我们再增加对于语句的处理。

P -> D E

D -> T id; D

   |

T -> int

   |   bool

S -> id = E

   |   printi(E)

   |   printb(E)

E -> n

   |   id

   |   true

   |   false

   |   E + E

   |   E && E

ps：P为程序，D为变量声明，S为语句，T为变量类型，E为表达式 

新增的检查statement函数伪代码如下： 

void check_stm(Table_t table, Stm_t s)
{switch (s->kind){case STM_ASSIGN:t1 = Table_lookup(s->id);t2 = check_exp(table, s->exp);if (t1 != t2)error("type mismatch");else return INT;case STM_PRINTI:t = check_exp(s->exp);if (t != INT)error("type mismatch");else return ;case STM_PRINTB:t = check_exp(s->exp);if (t != BOOL)error("type mismatch");else return ;default:break;}
}