1、状态压缩入门题：Leetcode 464. 我能赢吗

1.1 题目描述

在 “100 game” 这个游戏中，两名玩家轮流选择从 1 到 10 的任意整数，累计整数和，先使得累计整数和 达到或超过 100 的玩家，即为胜者。

如果我们将游戏规则改为 “玩家 不能 重复使用整数” 呢？

例如，两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数（不放回），直到累计整数和 >= 100。

给定两个整数 maxChoosableInteger （整数池中可选择的最大数）和 desiredTotal（累计和），若先出手的玩家能稳赢则返回 true ，否则返回 false 。假设两位玩家游戏时都表现 最佳 。

示例 1：

输入：maxChoosableInteger = 10, desiredTotal = 11
输出：false
解释：
无论第一个玩家选择哪个整数，他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1，那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10（那么累积和为 11 >= desiredTotal），从而取得胜利.
同样地，第一个玩家选择任意其他整数，第二个玩家都会赢。

示例 2：

输入：maxChoosableInteger = 10, desiredTotal = 0
输出：true

示例3：

输入：maxChoosableInteger = 10, desiredTotal = 1
输出：true

提示:

• 1 <= maxChoosableInteger <= 20
• 0 <= desiredTotal <= 300

1.2 思路分析

• 暴力解

class Solution {//超时//时间复杂度O(N!)：先手可进行的尝试 1 ~ N，后手可进行的尝试1 ~ N-1, 先手可进行的尝试 1 ~ N-2  ...public boolean canIWin(int maxChoosableInteger, int desiredTotal) {if (desiredTotal == 0) { //题意规定return true;}if ((maxChoosableInteger * (maxChoosableInteger + 1) >> 1) < desiredTotal) {//给定的整数池中的所有数累加和都小于desiredTotalreturn false;}int[] arr = new int[maxChoosableInteger];for (int i = 0; i < maxChoosableInteger; i++) {arr[i] = i + 1;} // 如果 arr[i] != -1，表示该数还未被选择// 如果 arr[i] = -1, 表示该数已经被选择return process(arr, desiredTotal);}//当前轮到先手选择，只能选择arr中不为-1的数字//还剩rest这个累加和//返回先手是否会赢public static boolean process(int[] arr, int rest) {if (rest <= 0) { //先手先面对<=0的情况，先手输了return false;}//先手尝试所有情况for (int i = 0; i < arr.length; i++) {if (arr[i] != -1) { //可选择的数字//先手的决定！int cur = arr[i];arr[i] = -1;//当前的先手在子过程里是后手boolean next = process(arr, rest - cur);arr[i] = cur; //恢复现场if (!next) {  //子过程的先手输了return true;}} }return false;}
}

递归函数 process 中的 arr 会影响返回的结果。这个可变参数是个线性结构，表示了某个数是否存在的状态，其复杂程度突破了整型。

举个例子：maxChoosableInteger = 4，rest = 5，即可拿的数字数字[1,2,3,4]

• 先手拿走1，则数组变成 [-1，2，3，4]， rest = 4；后手拿走2，则数组变成 [-1， -1，3，4]，rest = 2
• 先手拿走2，则数组变成 [1，-1，3，4]， rest = 3；后手拿走1，则数组变成 [-1，-1，3，4]，rest = 2

可见，先选择 $a$ 再选择 $b$，或者先选择 $b$ 再选择 $a$，两条分支面对同一个后续过程，那么做缓存就有利可图。

题目给定的数据范围1 <= maxChoosableInteger <= 20比较小，可以使用整型 int 的位信息，表示某个数是否存在，也就是说用一个整型变量的位信息替代线性结构。

• 暴力解：位信息替代线性结构

于是，可以改写成如下代码：

//超时
class Solution {public boolean canIWin(int maxChoosableInteger, int desiredTotal) {//题意规定if (desiredTotal == 0) { return true;}//给定的整数池中的所有数累加和都小于desiredTotalif ((maxChoosableInteger * (maxChoosableInteger + 1) >> 1) < desiredTotal) {return false;}return process(maxChoosableInteger, 0, desiredTotal);}//当前轮到先手选择，可以选择1 ~ maxChoosableInteger中的任意数字//status：i位如果为0，代表没被选择过，当前可选择；i位如果为1，代表已被选择，当前不可选//还剩rest这么多累加和需要凑//返回先手会不会赢public static boolean process(int maxChoosableInteger, int status, int rest) {if (rest <= 0) { //先手输了return false;}for (int i = 1; i <= maxChoosableInteger; i++) {if (((1 << i) & status) == 0) { //i这个数字是此时先手的决定，判断当前数字i是否可选，只有在status的第i位为0的时候才表示可选择if (!process(maxChoosableInteger, (status | (1 << i)), rest - i)) {//status | (1 << i)：将选择后的i这个数在status中的第i位标记为1return true;}}}return false;}
}

此时的递归函数process中，maxChoosableInteger 是固定参数，status 和 rest 是可变参数，可以搞动态规划/记忆化搜索。

status 的状态可以决定 rest：例如可选的数字 [1，2，3，4，5]，rest = 10，如果status的状态位中第2位和第4位的值都是1，则rest的值一定是 10 - (2 + 4) = 4；如果status的状态位中第3位和第5位的值都是 1，则rest的值一定是 10 - (3 + 5) = 2。于是，一维动态规划表即可，只需要对 status 做缓存。改写为如下的动态规划版本。

• 动态规划

假设给定的maxChoosableInteger = 5，如果位信息中第0位弃而不用，第1位存放数字1是否被选择的信息，第2位存放数字2是否被选择的信息，…，那么一共需要 6 个二进制位，这6个二进制位能表示的状态最大值就是 111111（二进制形式），那么需要准备一张规模为 1<<(maxChoosableInteger + 1) = 1000000 的表才能将 000000 ~ 111111 (二进制形式）这些数全部放下。

//通过
//时间复杂度：如果maxChoosableInteger = N，则status可以表示 2^N 种状态，这N个数会被变成N位
//所以数组要准备 2^N 的长度
//对应每一种状态要经历 N 次的枚举
//所以时间复杂度为 O(2^N * N)，优于O(N!)的复杂度
class Solution {public boolean canIWin(int maxChoosableInteger, int desiredTotal) {//题意规定if (desiredTotal == 0) { return true;}//给定的整数池中的所有数累加和都小于desiredTotalif ((maxChoosableInteger * (maxChoosableInteger + 1) >> 1) < desiredTotal) {return false;}//假设maxChoosableInteger = 5//准备这个dp表来存放 000000 ~ 111111 这些数//规模 1<<(5+1) = 1000000，对应的下标就是 000000 ~ 111111int[] dp = new int[1 << (maxChoosableInteger + 1)];//dp[status] == 1, 表示status作为参数的过程计算过了，结果是true//dp[status] == -1, 表示status作为参数的过程计算过了，结果是false//dp[status] = 0, 表示status作为参数的过程process(status)没有计算过，去计算return process(maxChoosableInteger, 0, desiredTotal, dp);}//status和rest是两个可变参数，但是rest是由status决定的，因为选了一批数字之后，得到的和一定是一样的//所以只用status来代表状态（即dp），只需要对status做缓存，rest不需要参与记忆化搜索public static boolean process(int maxChoosableInteger, int status, int rest, int[] dp) {if (dp[status] != 0) { return dp[status] == 1 ? true : false;}boolean ans = false;if (rest > 0) {for (int i = 1; i <= maxChoosableInteger; i++) {if (((1 << i) & status) == 0) {if (!process(maxChoosableInteger, (status | (1 << i)), rest - i, dp)) {ans = true;break;}}}}dp[status] = ans ? 1 : -1;return ans;}}

1.3 小结

本题是状态压缩的入门题，说明了某一种情况：如果对于一个函数，它的可变参数是一个线性结构（如本题的arr数组），但是它表示的是某个位置存在或不存在，可以将其转成整型，虽然转成了整型，但是其实质还是线性结构。

这已经突破了之前讲过的「暴力递归设计原则」，这种需要进行状态压缩的题目可以通过「数据限制」得到提醒。
本题的优化后的时间复杂度O(2N∗N)O(2^N * N)O(2N∗N)，对于给定的数据范围最大值20，结果为 O(220∗20)<108O(2^{20} * 20) < 10^8O(220∗20)<108，对于这种数据量小的题目，可能是「分治」，可能是「状态压缩的动态规划」。

2、状态压缩经典问题：TSP问题

2.0 TSP问题概述

TSP，即旅行商问题，又称TSP问题（Traveling Salesman Problem），是数学领域中著名问题之一。

假设有一个旅行商人要拜访N个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。TSP问题是一个NPC问题。

2.1 题目描述

有 $N$ 个城市，任意两个城市之间都有距离，任何一座城市到自己的距离都为0。所有点到点的距离都存放在一个 $N\times N$ 的二维数组 matrix里，也就是整张图由邻接矩阵表示。

现要求一旅行商从 $k$ 城市出发必须经过每一个城市且只在一个城市逗留一次，最后回到出发的 $k$ 城，返回总距离最短的路的距离。

参数给定一个 matrix，给定 $k$。

2.2 思路分析

该图是无向图，即A到B的距离和B到A的距离相等，又城市到自己的距离为0，所以该矩阵就是一个对角线为0，且关于对角线对称的矩阵。从 $k$ 城出发最后要回到 $k$ 城，则整个过程是一个环，所以出发点是哪个城市不重要。

2.3 代码实现

• 暴力解

public class TSP {public static int t1(int[][] matrix) {int N = matrix.length; // 0...N-1// set// set.get(i) != null i这座城市在集合里// set.get(i) == null i这座城市不在集合里List<Integer> set = new ArrayList<>();for (int i = 0; i < N; i++) {set.add(1); //如果i城市没有被访问过，则i位置对应的值为1，否则对应的值为null//假设有0、1、2、3、4、5座城市，则set中的信息是{1, 1, 1, 1, 1, 1}}return func1(matrix, set, 0); //从0出发，同时意味着0是所有子过程的归宿点}// 任何两座城市之间的距离，可以在matrix里面拿到// set中表示着哪些城市的集合，// start这座城一定在set里，// 从start出发，要把set中所有的城市过一遍，最终回到0这座城市，最小距离是多少public static int func1(int[][] matrix, List<Integer> set, int start) {//统计set中还剩几座城int cityNum = 0;for (int i = 0; i < set.size(); i++) { if (set.get(i) != null) {cityNum++;}}//base case//集合中只剩一座城，则直接从该城回到归宿点0，即matrix[start][0]if (cityNum == 1) {return matrix[start][0];}//因为在只有1座城的时候返回了，所以cityNum必然不会<1// 此时cityNum > 1，即不只start这一座城set.set(start, null); //先将自己从集合中去除，因为自己这座城已经访问过int min = Integer.MAX_VALUE;for (int i = 0; i < set.size(); i++) { //遍历所有从start能去的城市if (set.get(i) != null) {// start -> i i... -> 0int cur = matrix[start][i] + func1(matrix, set, i); min = Math.min(min, cur);}}set.set(start, 1);//还原现场return min;}
}

在 func1 函数中有2个可变参数set 和 start，如果想要改成动态规划，得需要这2个可变参数组出来的子过程有重复解，如果没有重复解，就没有搞缓存的必要。

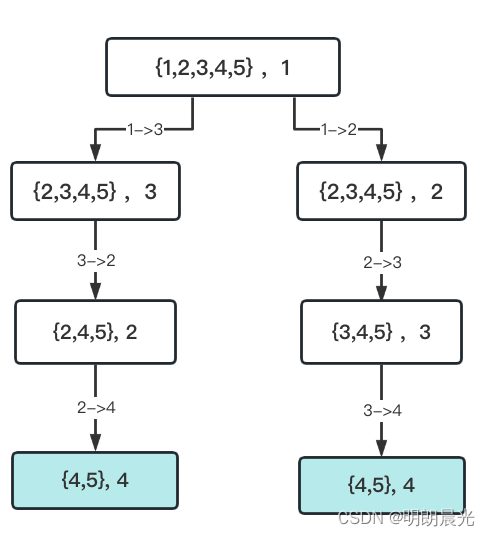
可见，是做三个决定后才展现了重复解，但是也是存在重复解的。

• 用位信息表示城市被访问的状态

public class TSP {public static int t2(int[][] matrix) {int N = matrix.length; // 0...N-1// 7座城，对应的位信息：1111111int allCity = (1 << N) - 1;return f2(matrix, allCity, 0);}// 任何两座城市之间的距离，可以在matrix里面拿到// set中表示着哪些城市的集合，// start这座城一定在set里，// 从start出发，要把set中所有的城市过一遍，最终回到0这座城市，最小距离是多少// cityStatus：位信息表示城市的情况，用int整型变量取代线性结构setpublic static int f2(int[][] matrix, int cityStatus, int start) {//只有一座城了，该城就是start，就直接返回if (cityStatus == (cityStatus & (~cityStatus + 1))) { //取出最右侧的1，如果和自己相等，则二进制中只有一个1，也就是只剩一座城return matrix[start][0];}// 把start位的1去掉，cityStatus &= (~(1 << start));int min = Integer.MAX_VALUE;// 枚举所有的城市for (int move = 0; move < matrix.length; move++) {if ((cityStatus & (1 << move)) != 0) {int cur = matrix[start][move] + f2(matrix, cityStatus, move);min = Math.min(min, cur);}}cityStatus |= (1 << start); //恢复现场return min;}
}

• 记忆化搜索/傻缓存

public class TSP {public static int t3(int[][] matrix) {int N = matrix.length; // 0...N-1// 7座城 1111111int allCity = (1 << N) - 1;int[][] dp = new int[1 << N][N];for (int i = 0; i < (1 << N); i++) {for (int j = 0; j < N; j++) {dp[i][j] = -1;}}return f3(matrix, allCity, 0, dp);}// 任何两座城市之间的距离，可以在matrix里面拿到// set中表示着哪些城市的集合，// start这座城一定在set里，// 从start出发，要把set中所有的城市过一遍，最终回到0这座城市，最小距离是多少// cityStatus和start共同决定返回值，所以dp是二维的public static int f3(int[][] matrix, int cityStatus, int start, int[][] dp) {if (dp[cityStatus][start] != -1) {//该过程已经计算过，则直接从缓存中取值return dp[cityStatus][start];}if (cityStatus == (cityStatus & (~cityStatus + 1))) {dp[cityStatus][start] = matrix[start][0];} else {// 把start位的1去掉，cityStatus &= (~(1 << start));int min = Integer.MAX_VALUE;// 枚举所有的城市for (int move = 0; move < matrix.length; move++) {if (move != start && (cityStatus & (1 << move)) != 0) {int cur = matrix[start][move] + f3(matrix, cityStatus, move, dp);min = Math.min(min, cur);}}cityStatus |= (1 << start);dp[cityStatus][start] = min;}return dp[cityStatus][start];}
}

• 动态规划

public class TSP {public static int t4(int[][] matrix) {int N = matrix.length; // 0...N-1int statusNums = 1 << N;int[][] dp = new int[statusNums][N];for (int status = 0; status < statusNums; status++) {for (int start = 0; start < N; start++) {if ((status & (1 << start)) != 0) {if (status == (status & (~status + 1))) {dp[status][start] = matrix[start][0];} else {int min = Integer.MAX_VALUE;// start 城市在status里去掉之后，的状态int preStatus = status & (~(1 << start));// start -> ifor (int i = 0; i < N; i++) {if ((preStatus & (1 << i)) != 0) {int cur = matrix[start][i] + dp[preStatus][i];min = Math.min(min, cur);}}dp[status][start] = min;}}}}return dp[statusNums - 1][0];}
}

2.4 小结

线性结构中的每个值如果表示的是在或不在两种状态，则可以用位信息来表示，然后写成状态压缩的动态规划。

3、铺瓷砖

3.1 题目描述

你有无限的 $1\ast 2$ 的砖块，要铺满 $M\ast N$ 的区域，不同的铺法有多少种？

3.2 思路分析

本来对于区域内的任意一个位置，有上下左右四种铺法：

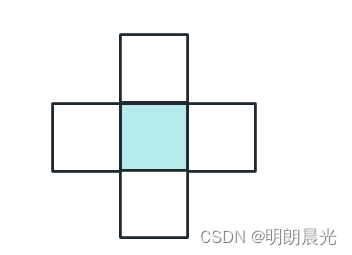
人为限制一下，任何一个位置只能向上或者向右铺。这样的限制并不会影响最终的方法数，因为该位置往下方铺瓷砖等同于下方往上铺，该位置往左铺，等同于左边位置向右铺，所以最终的方法数是不变的。

接下来设计递归函数：int f(int i, int pre, int N)

• 第一个参数 i 表示来到第 $i$ 行做决定，潜台词就是前 $i-2$ 行都已经铺满了；
• 第二个参数 pre，用位信息标记第 $i-1$ 行每个格子是否有瓷砖，即上一行的状态；
• 第三个参数 N，表示一共有多少行，是固定参数；
• 返回值表示由第 $i$ 行做出的决定最终能使得 0 ~ N-1 行全部铺满的方法数；
• base case：$i=N$，此时已经越界，无法再做决定，此时当 pre 的状态是全1的时候，表示找到了一种有效方法，返回1，否则返回0。

第 $i$ 行如何做决策取决于上一行的状态，如

i-1行：空 空 有 有 有 空 空i 行：上 上 右 右 右 上 上

当 $i-1$ 行的格子为空的时候，$i$ 行只能往上。

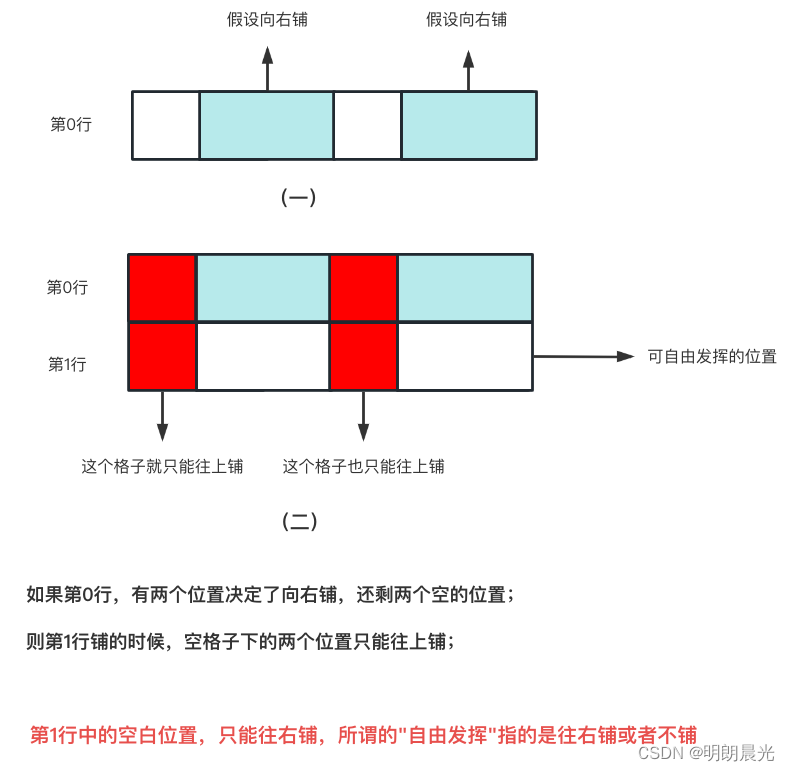
所以，如果上一行的状态pre = 01101100 (1代表有砖，0代表无砖），那么当前行的某些位置就固定为 10010011，其中0的位置表示可以自由发挥，对这些位置做「深度优先遍历」：

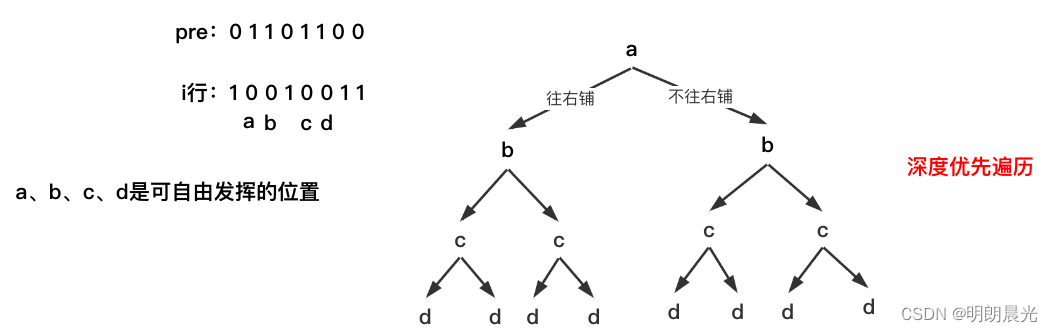
把每一种出现的决定往下行传。

3.3 代码实现

• 使用数组保存行状态

public class PavingTile {public static int ways1(int N, int M) {if (N < 1 || M < 1 || ((N * M) & 1) != 0) {return 0;}if (N == 1 || M == 1) {return 1;}int[] pre = new int[M]; // pre代表-1行的状况，此处使用的数组表示瓷砖状态，元素就是0或者1for (int i = 0; i < pre.length; i++) {pre[i] = 1;}return process(pre, 0, N);}// pre 表示level-1行的状态// level表示，正在level行做决定// N 表示一共有多少行 固定的// level-2行及其之上所有行，都摆满砖了// level做决定，让所有区域都满，方法数返回public static int process(int[] pre, int level, int N) {if (level == N) { // base casefor (int i = 0; i < pre.length; i++) { //检查上层的状态if (pre[i] == 0) {  //只要有一个位置是空，就表示没有将区域摆满，则这种方案失败return 0;}}return 1;}// 没到终止行，可以选择在当前的level行摆瓷砖int[] op = getOp(pre);//根据上一行的状态，决定此时能够进行的操作return dfs(op, 0, level, N);//op中为0的位置就是可以自由发挥的，利用深度优先遍历}public static int[] getOp(int[] pre) {int[] cur = new int[pre.length];for (int i = 0; i < pre.length; i++) {cur[i] = pre[i] ^ 1; //如果上一行状态是0，则当前状态为1；如果上一行状态是1，则当前状态为0}return cur;}// op[i] == 0 可以考虑摆砖// op[i] == 1 只能竖着向上//op为当前行所有的状态，col为到了第col列做决定，public static int dfs(int[] op, int col, int level, int N) {// 在列上自由发挥，玩深度优先遍历，当col来到终止列，i行的决定做完了if (col == op.length) {// 轮到i+1行，做决定return process(op, level + 1, N); //此时的op就是下一行level+1的上一行，子过程调用了父过程，但是行数增加了}int ans = 0;// 决定1：col位置不横摆ans += dfs(op, col + 1, level, N); // op没有变化，col位置上不摆瓷砖，去处理col+1位置// 决定2：col位置横摆, 向右if (col + 1 < op.length && op[col] == 0 && op[col + 1] == 0) {//当前col位置和 col+1 位置都是空的，则在col位置放一块砖向右铺，占据了col和col+1位置op[col] = 1;op[col + 1] = 1;//跳到col+2位置开始做决定ans += dfs(op, col + 2, level, N);//恢复现场op[col] = 0;op[col + 1] = 0;}return ans;}
}

• 使用位信息保存行状态

public class PavingTile {// Min (N,M) 不超过 32，才能用位信息表示，M 和 N 中较小的数做位运算public static int ways2(int N, int M) {if (N < 1 || M < 1 || ((N * M) & 1) != 0) {return 0;}if (N == 1 || M == 1) {return 1;}int max = Math.max(N, M);int min = Math.min(N, M);int pre = (1 << min) - 1;//max做行，min做列return process2(pre, 0, max, min);}// 上一行的状态，是pre，(1 << M) - 1是用来对齐的，N和M固定参数不用管// 当前来到i行，一共N行，返回填满的方法数public static int process2(int pre, int i, int N, int M) {if (i == N) { // base casereturn pre == ((1 << M) - 1) ? 1 : 0;}int op = ((~pre) & ((1 << M) - 1)); //根据上一行的状态pre，得到当前行的状态，0变1,1变0return dfs2(op, M - 1, i, N, M);//从i行的M-1列开始做决定}//当前行的状态是op//来到第col列，第level行public static int dfs2(int op, int col, int level, int N, int M) {if (col == -1) { //列数到-1列的时候终止return process2(op, level + 1, N, M);}int ans = 0;//情况1：当前位置不铺砖，则op没有变化，跳到下一列做决定ans += dfs2(op, col - 1, level, N, M);//情况2：往右铺if ((op & (1 << col)) == 0 /*当前col列位置的状态为0*/ && col - 1 >= 0/*后面还有列*/ && (op & (1 << (col - 1))) == 0 /*下一列的状态也是0*/) {//3 就是相邻的两个位置都变成了1//比如要二进制位的第6和第7位都变成1， 就是将二进制数11向左移动了6位，11000000，而11就是十进制的3ans += dfs2((op | (3 << (col - 1))), col - 2, level, N, M);}//注意，op是值传递，所以不用恢复现场return ans;}
}

• 记忆化搜索

// 记忆化搜索的解
public class PavingTile {// Min(N,M) 不超过 32public static int ways3(int N, int M) {if (N < 1 || M < 1 || ((N * M) & 1) != 0) {return 0;}if (N == 1 || M == 1) {return 1;}int max = Math.max(N, M);int min = Math.min(N, M);int pre = (1 << min) - 1;int[][] dp = new int[1 << min][max + 1];for (int i = 0; i < dp.length; i++) {for (int j = 0; j < dp[0].length; j++) {dp[i][j] = -1;}}return process3(pre, 0, max, min, dp);}public static int process3(int pre, int i, int N, int M, int[][] dp) {if (dp[pre][i] != -1) {return dp[pre][i];}int ans = 0;if (i == N) {ans = pre == ((1 << M) - 1) ? 1 : 0;} else {int op = ((~pre) & ((1 << M) - 1));ans = dfs3(op, M - 1, i, N, M, dp);}dp[pre][i] = ans;return ans;}public static int dfs3(int op, int col, int level, int N, int M, int[][] dp) {if (col == -1) {return process3(op, level + 1, N, M, dp);}int ans = 0;ans += dfs3(op, col - 1, level, N, M, dp);if (col > 0 && (op & (3 << (col - 1))) == 0) {ans += dfs3((op | (3 << (col - 1))), col - 2, level, N, M, dp);}return ans;}
}

• 严格位置依赖的动态规划

public class PavingTile {// 严格位置依赖的动态规划解public static int ways4(int N, int M) {if (N < 1 || M < 1 || ((N * M) & 1) != 0) {return 0;}if (N == 1 || M == 1) {return 1;}int big = N > M ? N : M;int small = big == N ? M : N;int sn = 1 << small;int limit = sn - 1;int[] dp = new int[sn];dp[limit] = 1;int[] cur = new int[sn];for (int level = 0; level < big; level++) {for (int status = 0; status < sn; status++) {if (dp[status] != 0) {int op = (~status) & limit;dfs4(dp[status], op, 0, small - 1, cur);}}for (int i = 0; i < sn; i++) {dp[i] = 0;}int[] tmp = dp;dp = cur;cur = tmp;}return dp[limit];}public static void dfs4(int way, int op, int index, int end, int[] cur) {if (index == end) {cur[op] += way;} else {dfs4(way, op, index + 1, end, cur);if (((3 << index) & op) == 0) { // 11 << index 可以放砖dfs4(way, op | (3 << index), index + 1, end, cur);}}}
}

广东高尔夫网