5.栈和队列

思考
一.什么是栈和队列?(What)
1.栈的定义和特点
1.栈定义:后进先出(LIFO)
2.栈的示意图
3.栈的应用
2.队列的定义和特点
1.队列定义:先进先出
2.队列的应用:
3.栈和队列特点
4.案例引入
1.栈
2.队列
5.栈的表示和操作实现
1.栈的抽象数据类型的类型定义
2.栈的操作(8种)
3.顺序栈
4.链栈
6.栈与递归
1.递归的定义
2.递归的三种应用场景
3.递归问题
7.队列的表示和操作实现
1.回顾
2.队列的抽象数据类型定义
二.为什么需要栈和队列?(Why)
1.栈的应用
2.队列的应用
三.如何学好栈和队列?(How)
数据结构很重要!
数据结构很重要!!!
数据结构很重要!!!!
思考
1.什么是栈和队列?(What)
2.为什么需要栈和队列?(Why)
3.如何学好栈和队列?(How)
注:特别感谢青岛大学王卓老师
第3章 栈和队列.pdf
一.什么是栈和队列?(What)
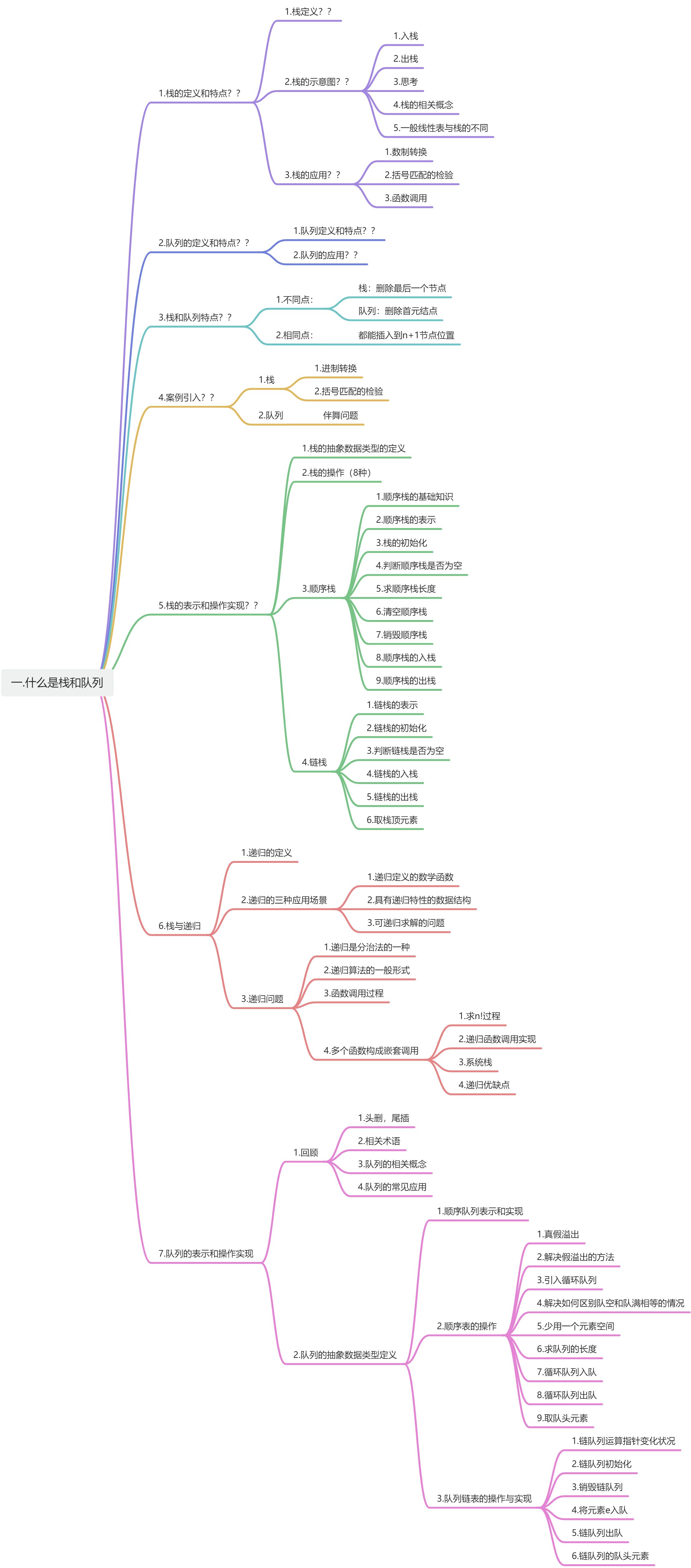
回顾线性表:
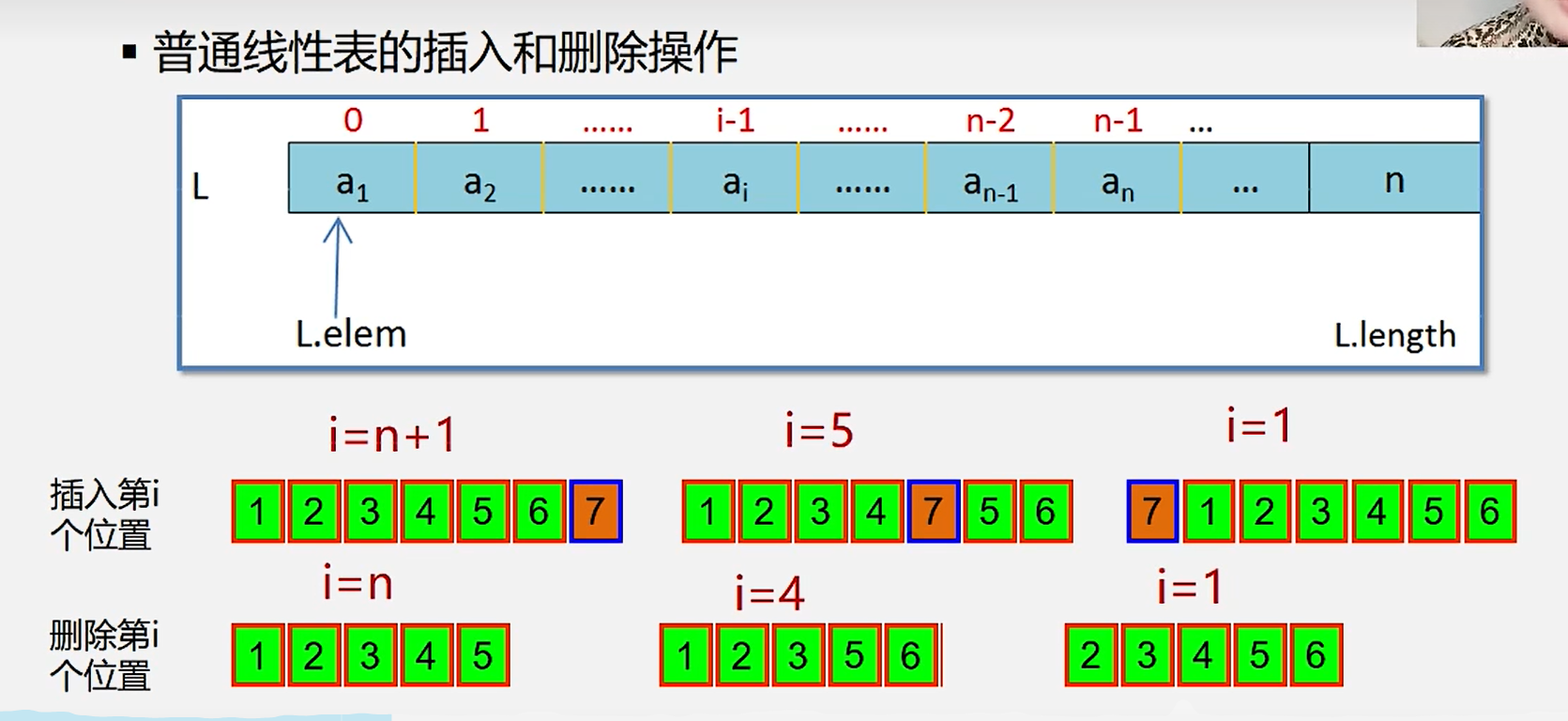
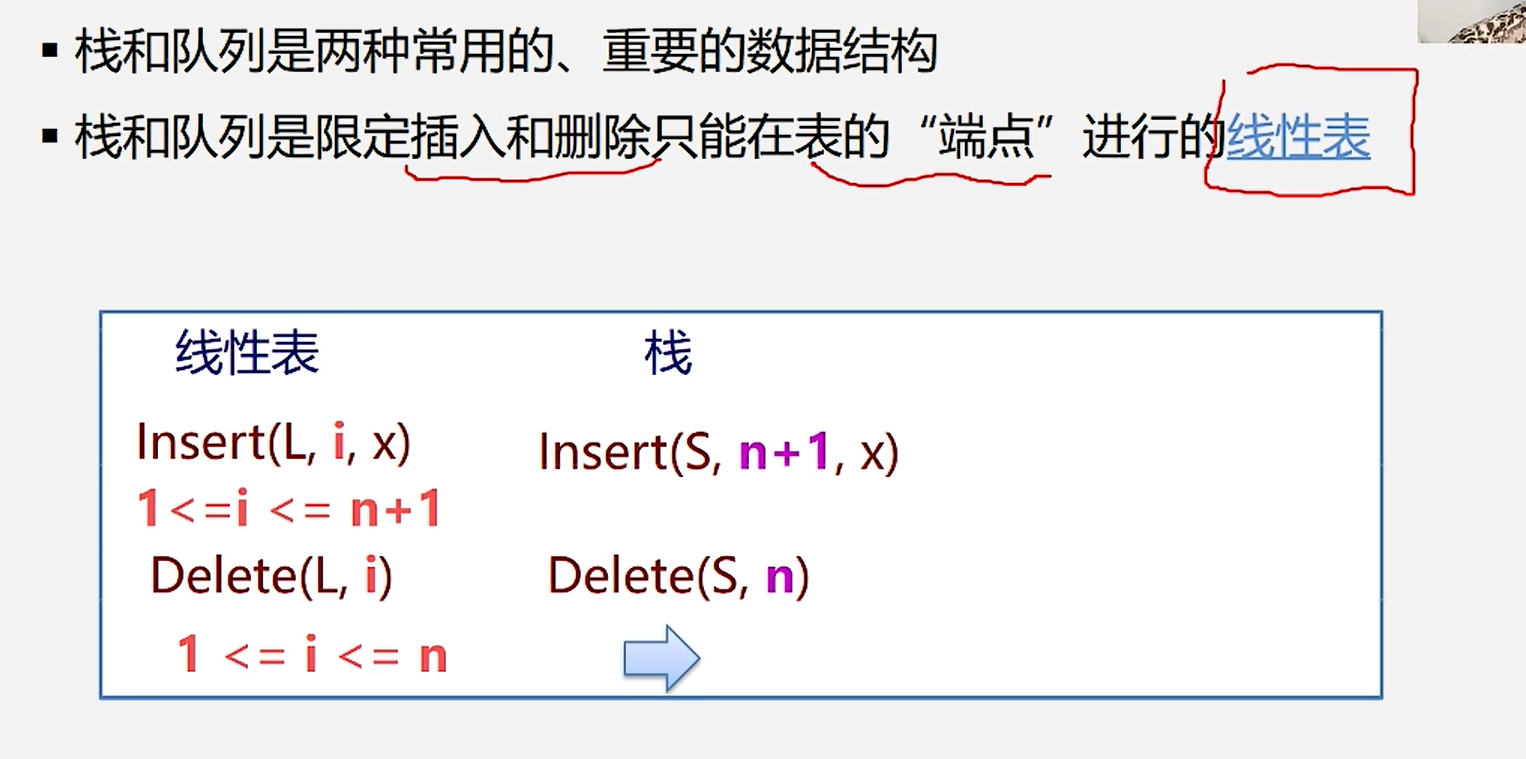
1.栈的定义和特点
1.栈定义:后进先出(LIFO)

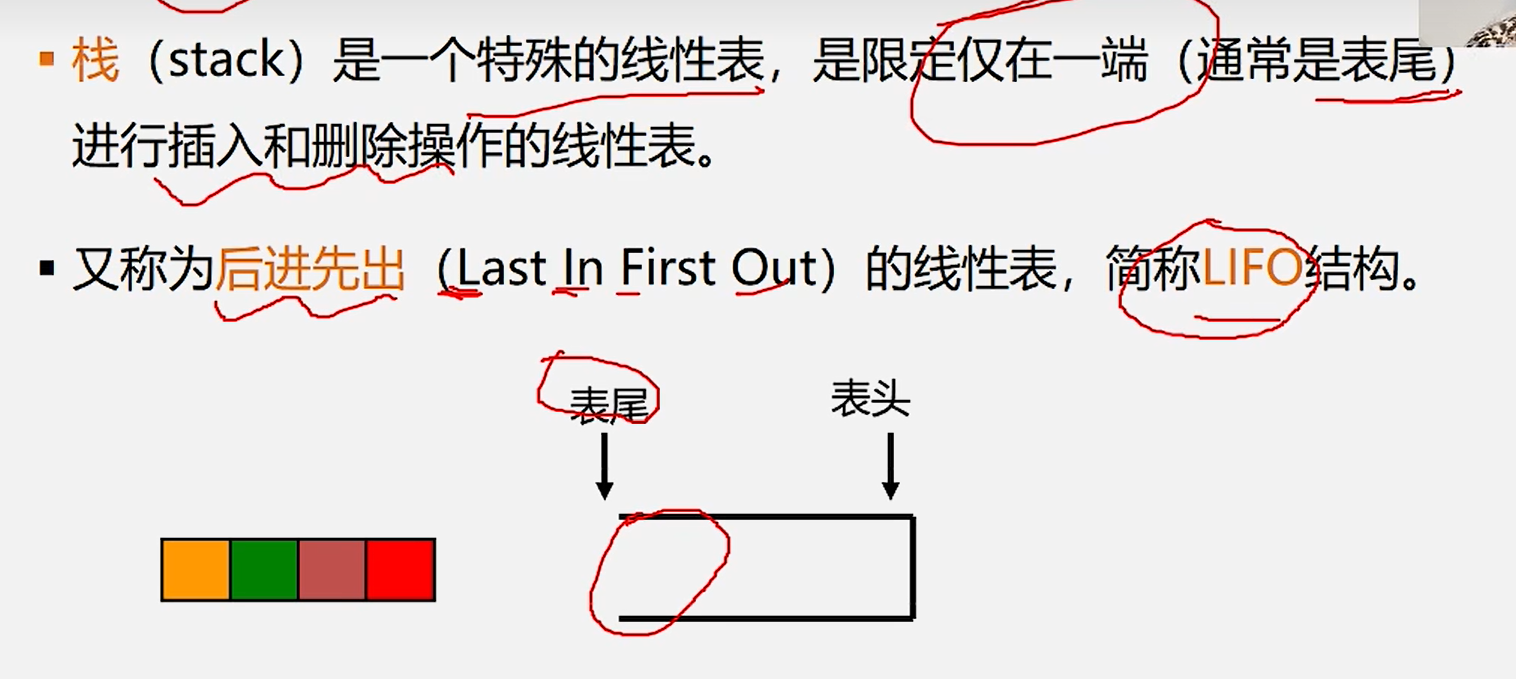

2.栈的示意图
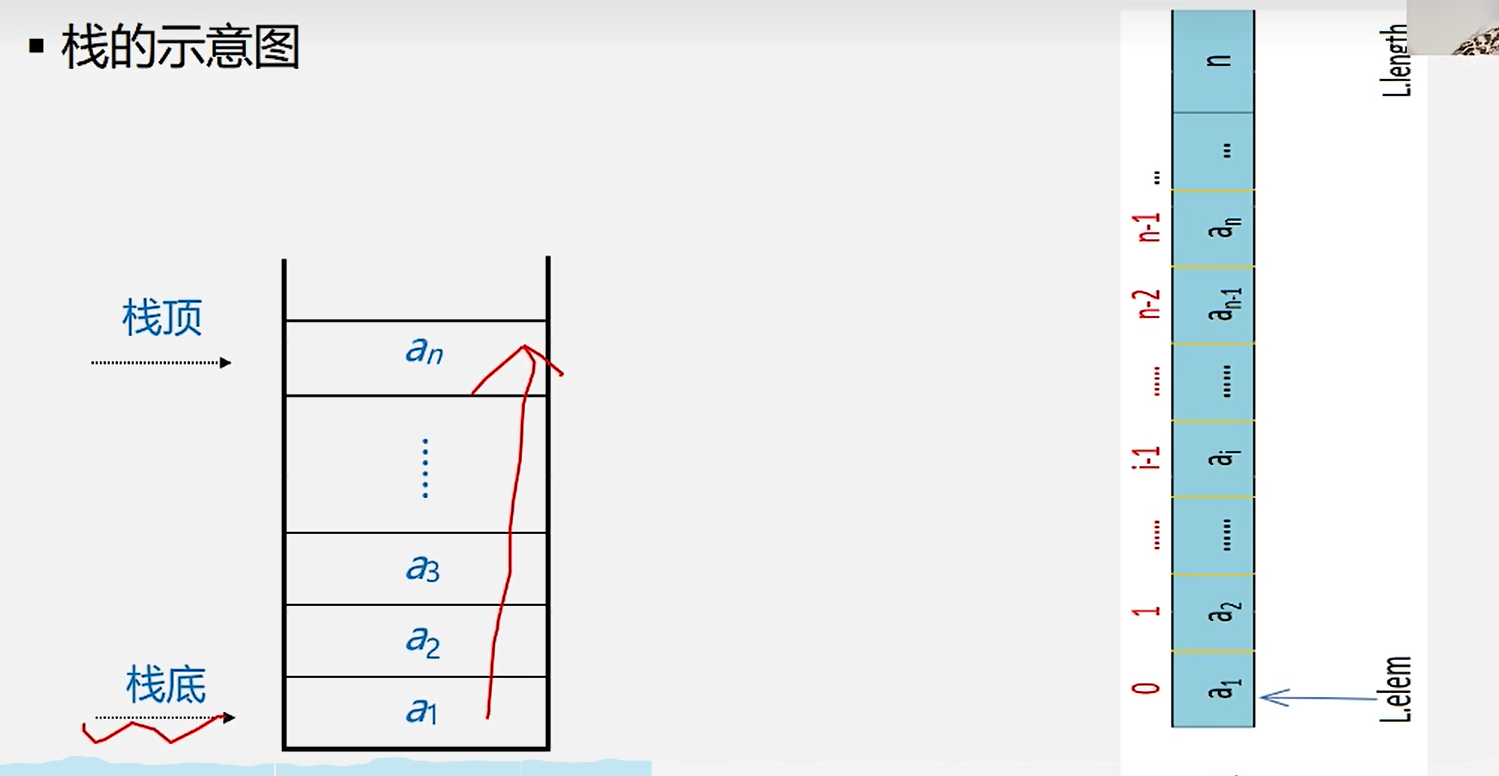
1.入栈:
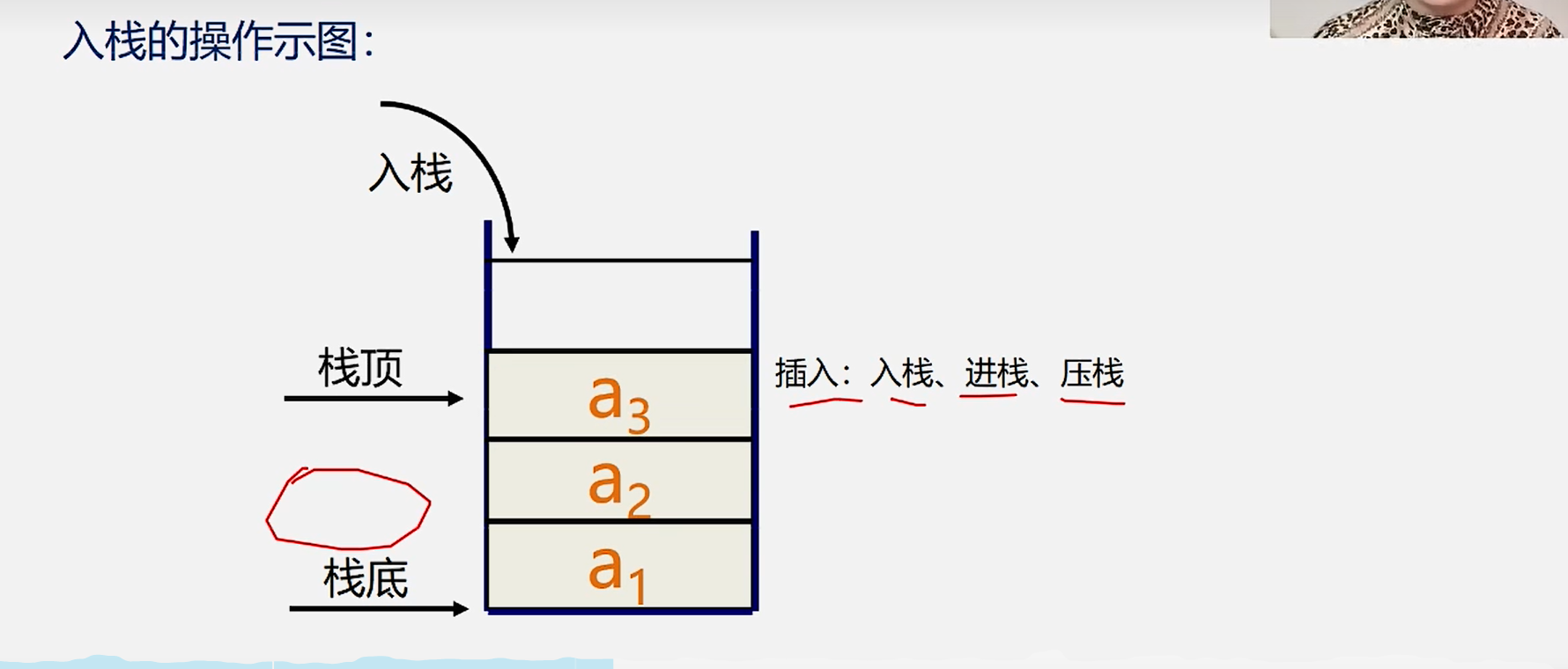
2.出栈:
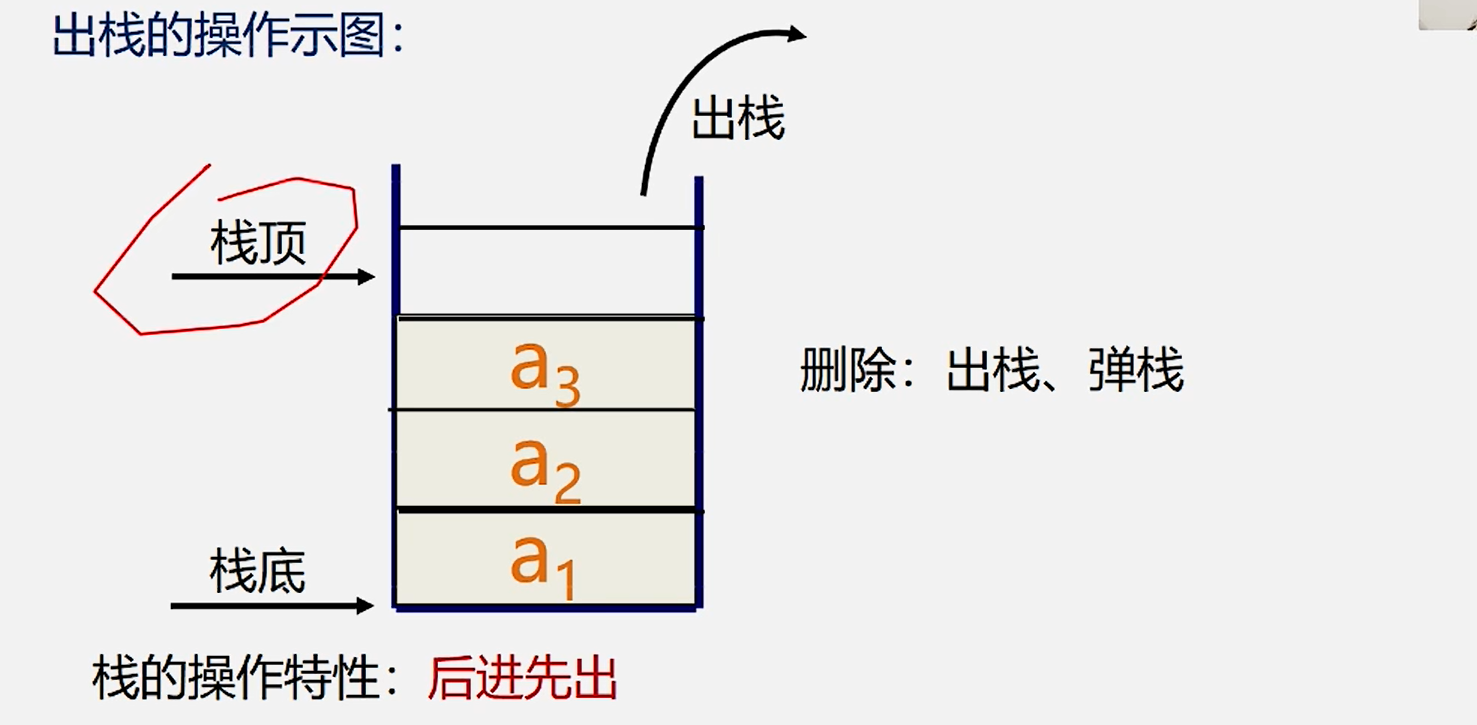
3.思考:

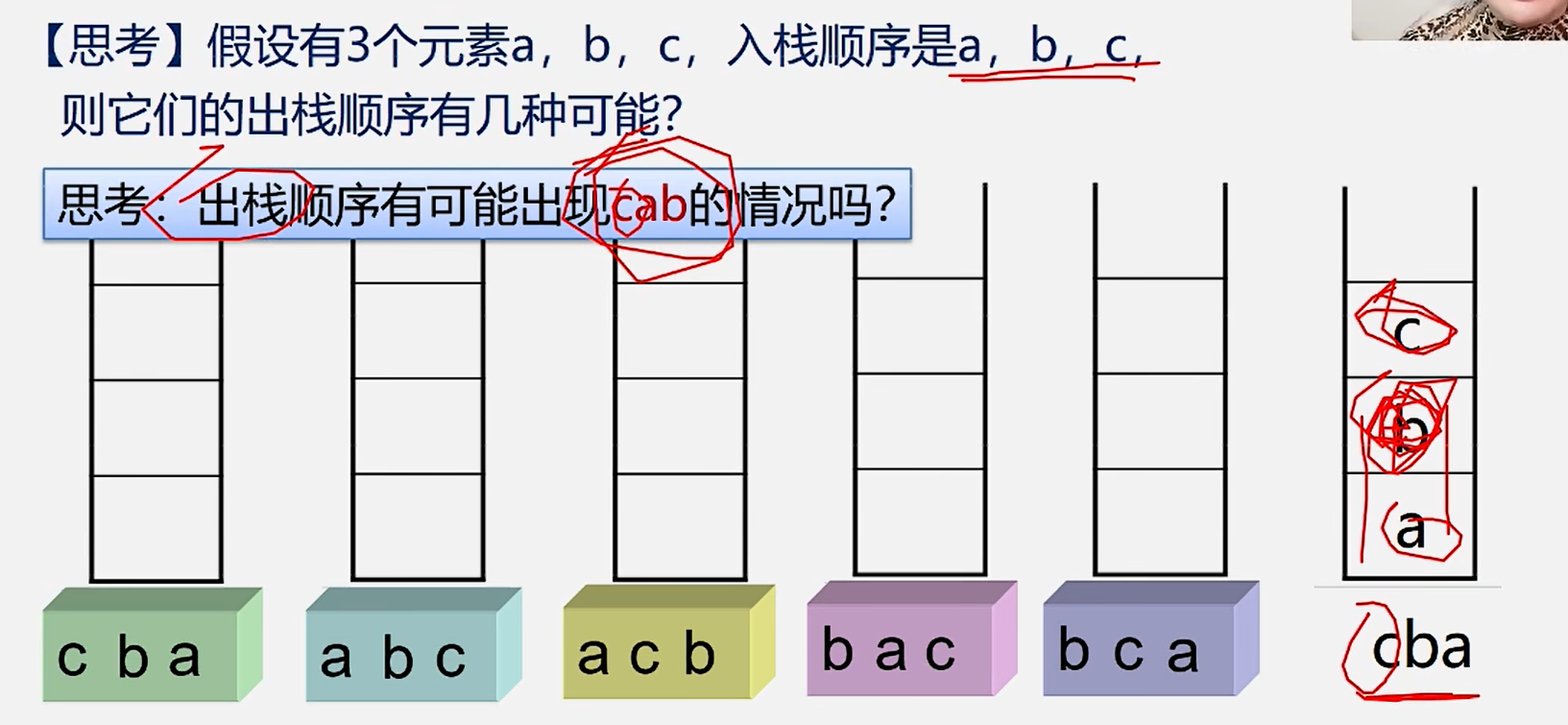
4.栈的相关概念:

5.一般线性表与栈的不同:

3.栈的应用

2.队列的定义和特点
1.队列定义:先进先出

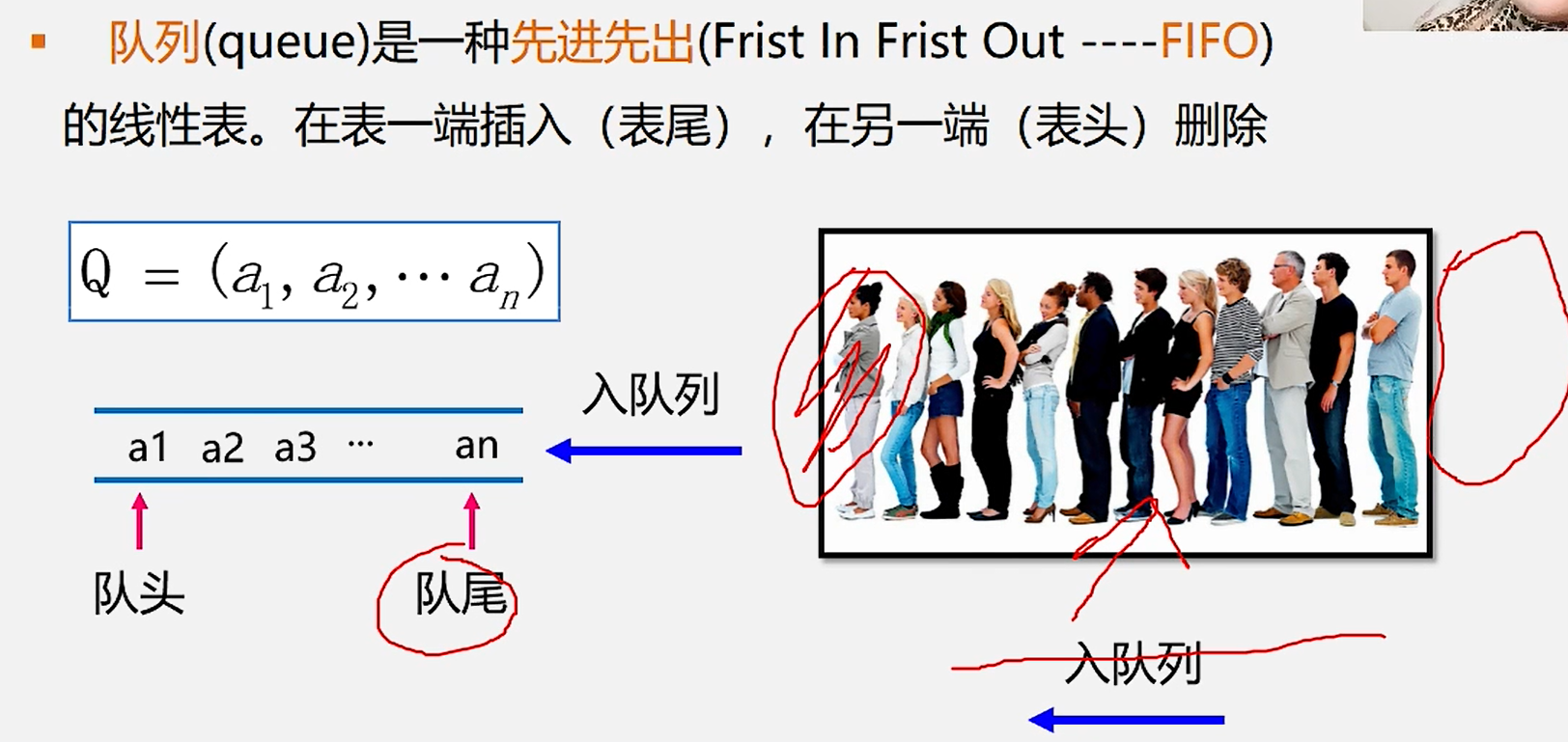

2.队列的应用:

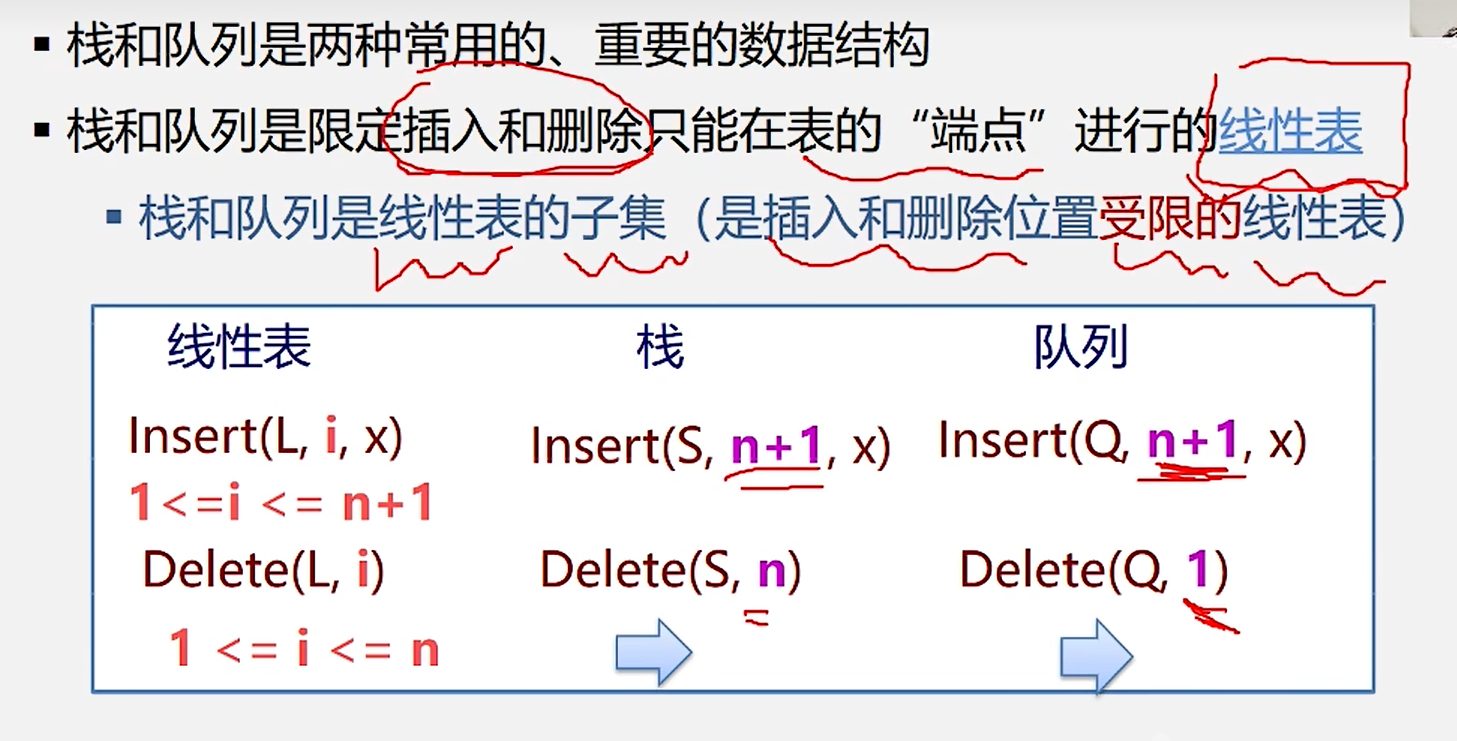
3.栈和队列特点
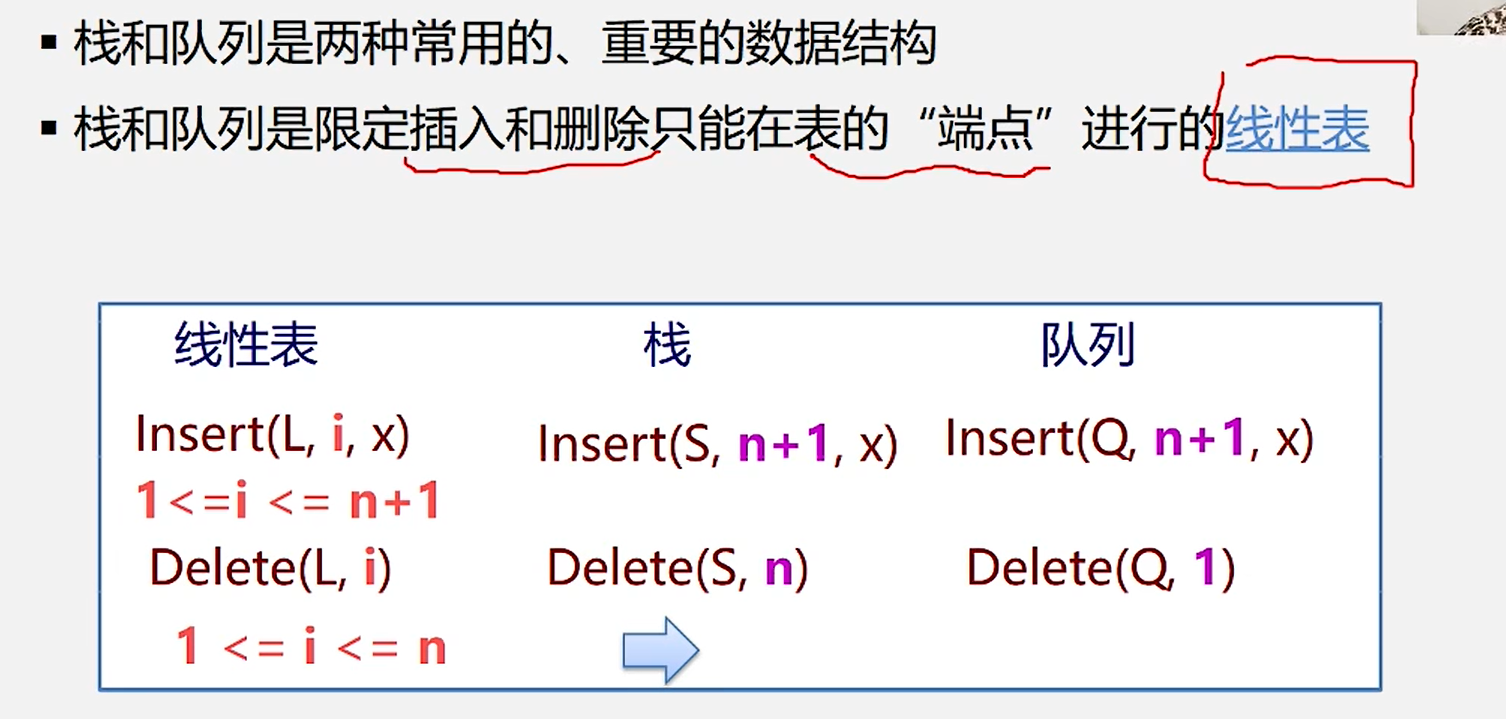
插入 删除
栈 n+1 n
队列 n+1 1
4.案例引入
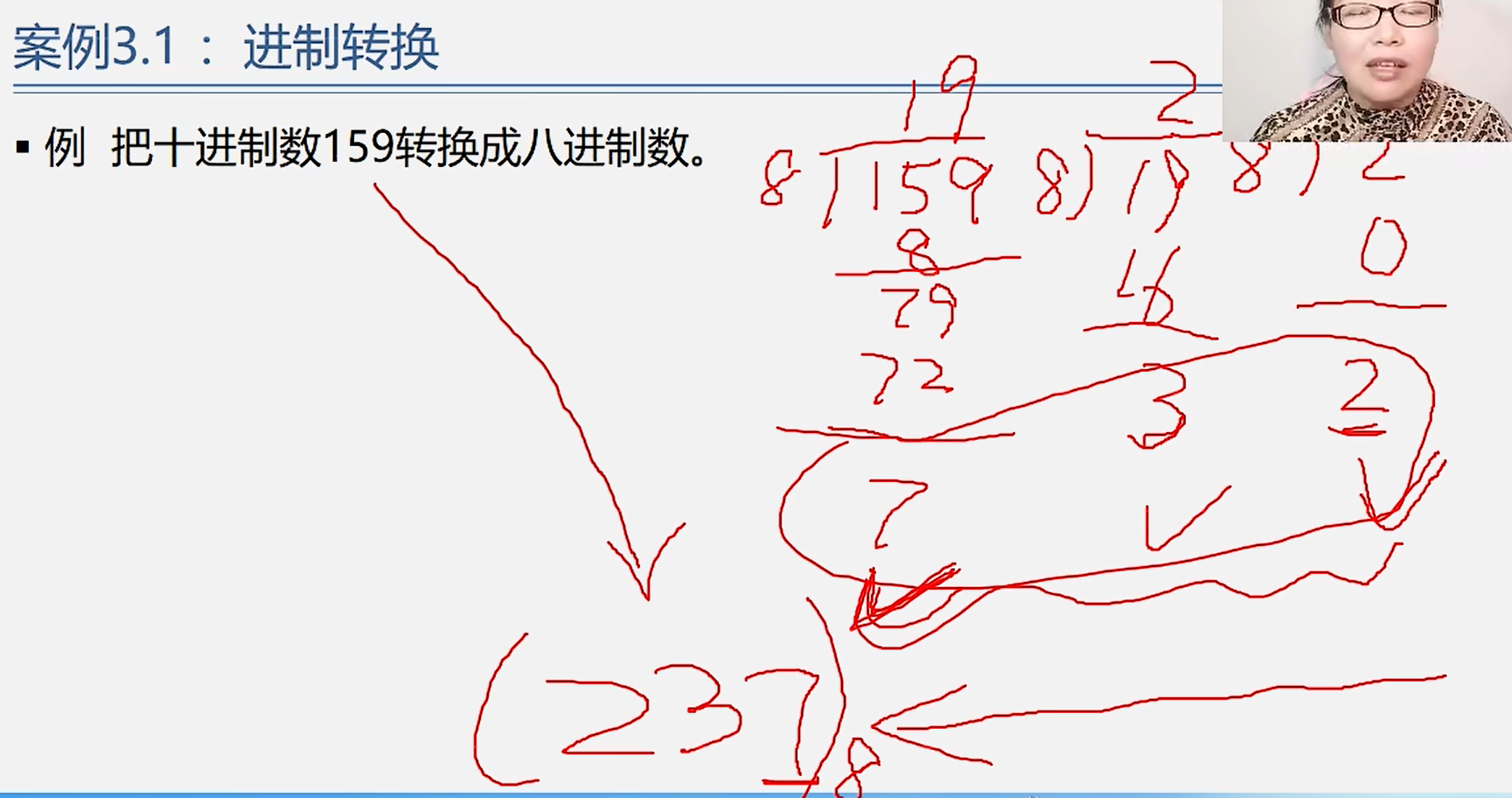
1.栈

1.进制转换

2.括号匹配的检验
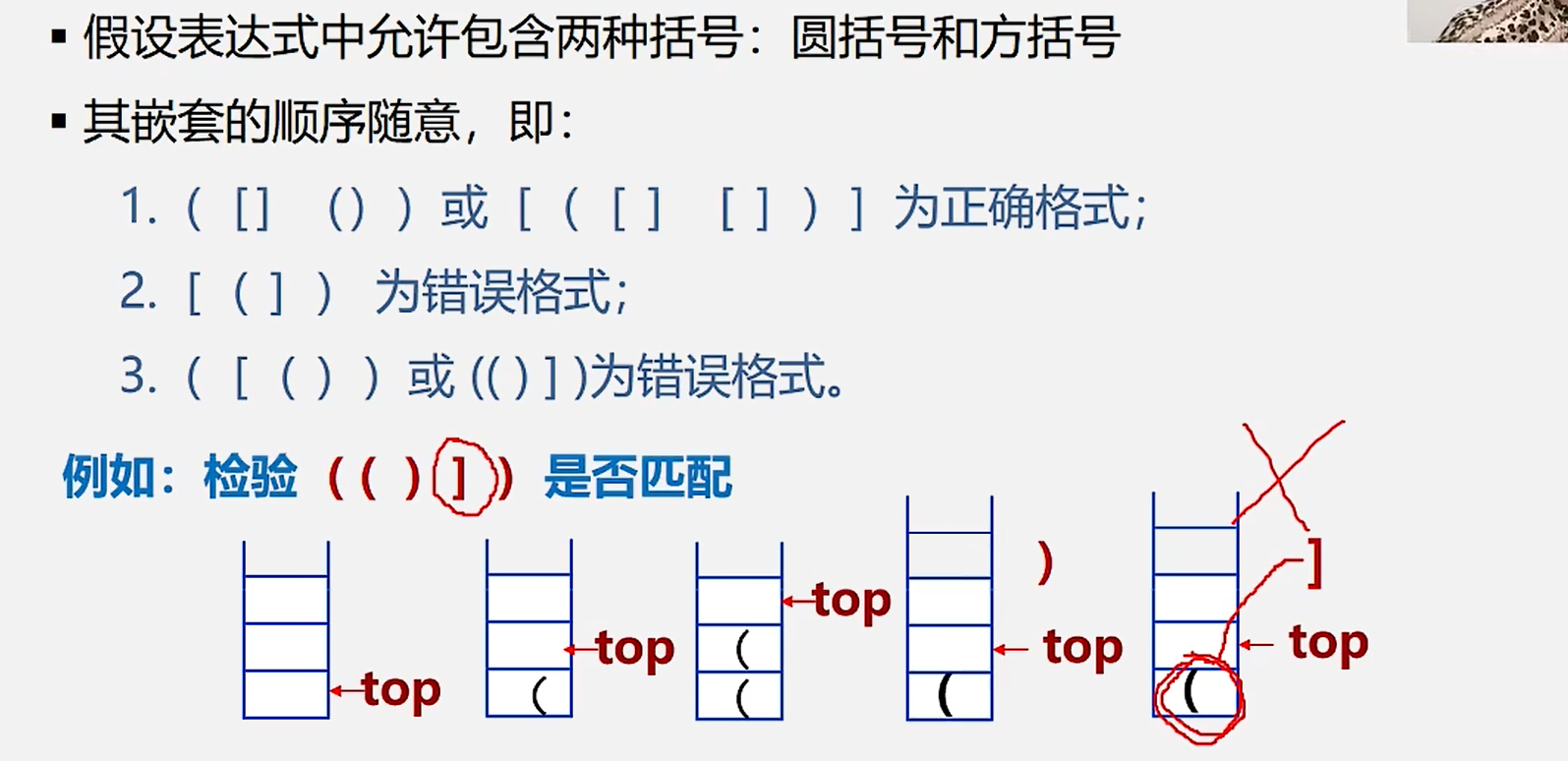


2.队列


5.栈的表示和操作实现
1.栈的抽象数据类型的类型定义

2.栈的操作(8种)

3.顺序栈

1.顺序栈的基本知识
1.栈的存储方式:用数组存储,top是栈顶,base是栈低

2.空栈:base==top
3.栈满:top=stacksize
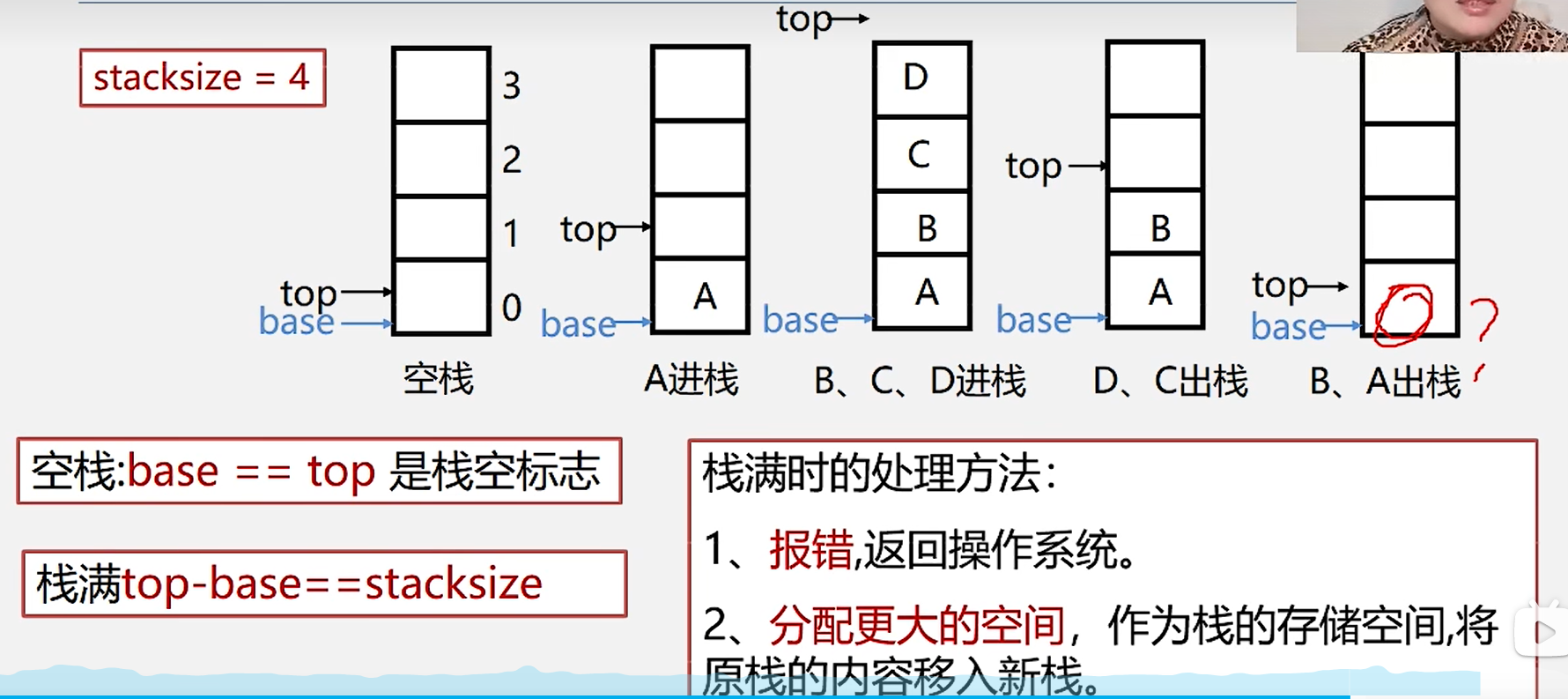
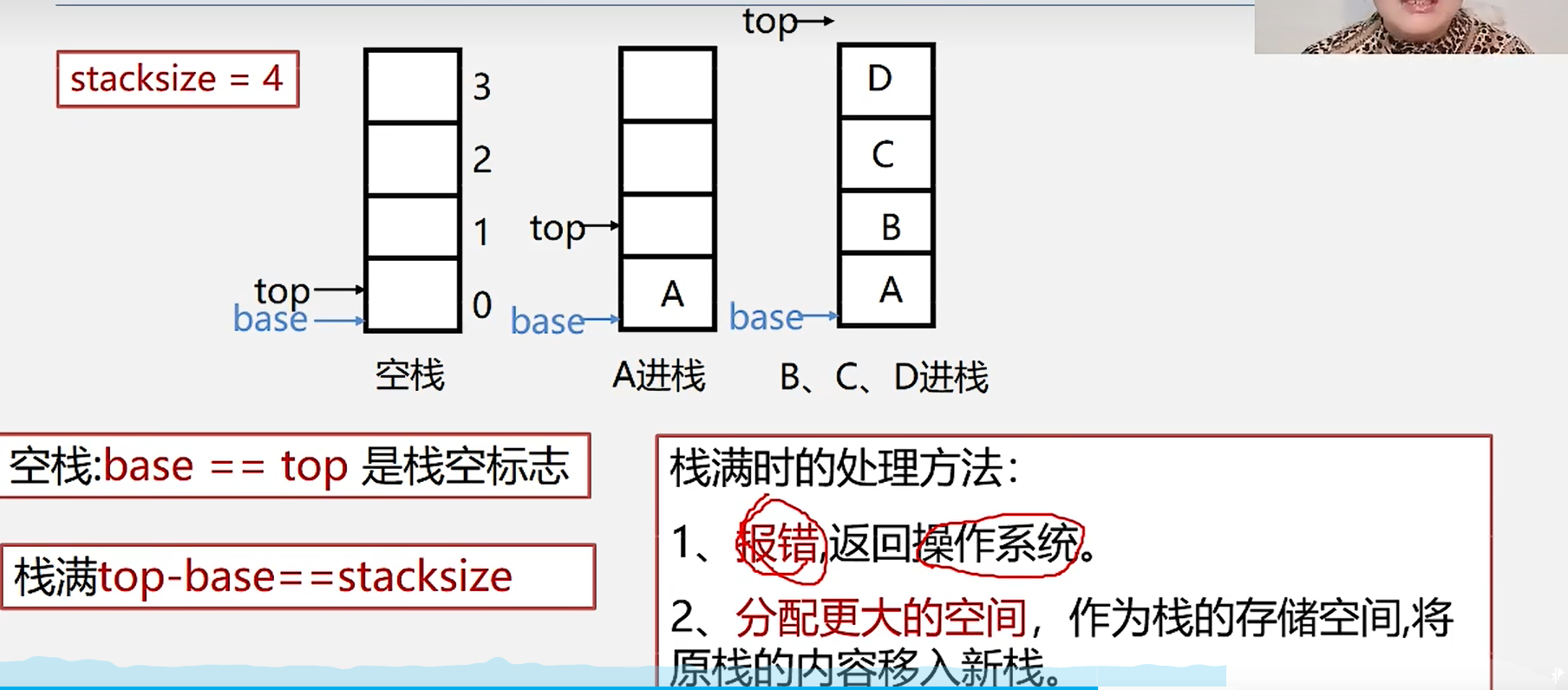
4.上溢:栈已经满了,又要压入元素
5.下溢:栈已经空了,还要弹出元素

2.顺序栈的表示:

注:俩个指针加减(同一数组)/也可以用数组下标=算这俩个元素之间差几个元素。
1.计算栈中元素个数

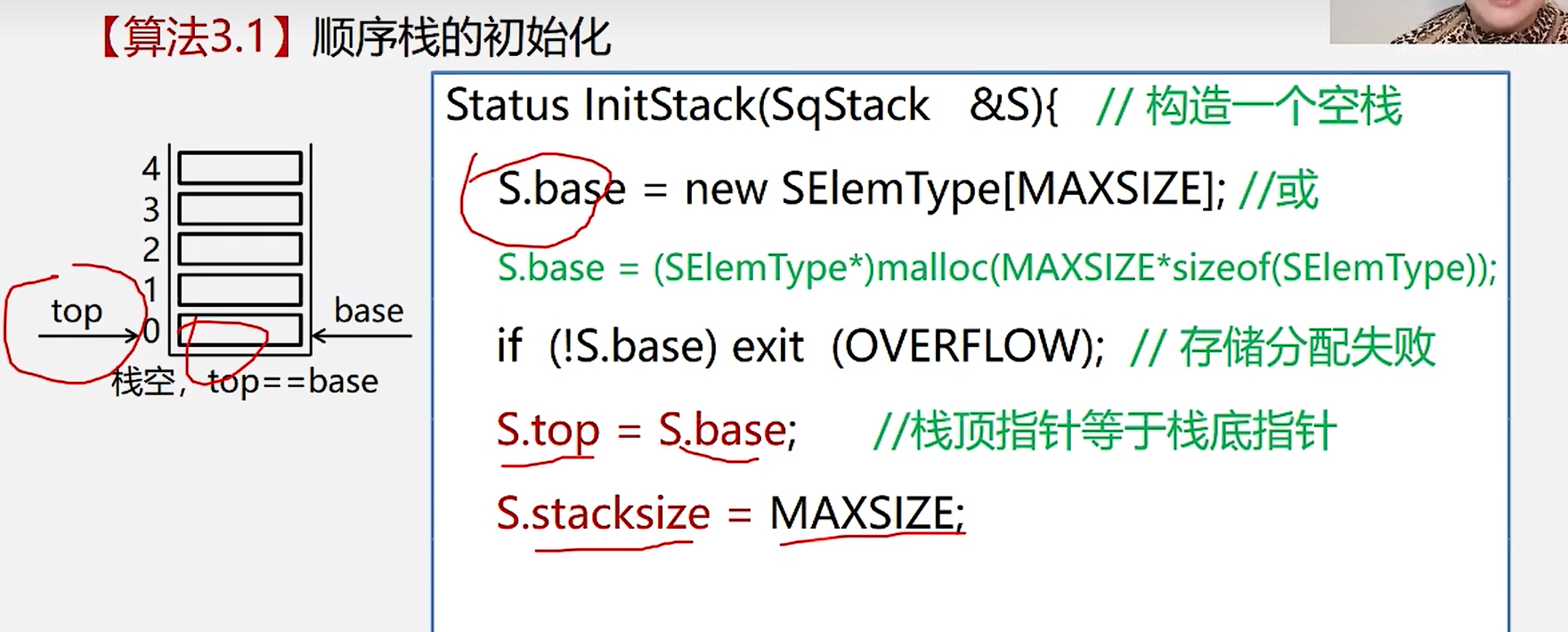
3.栈的初始化
Status InitStack(SqStack &S){
1.开辟一个新的数组
S.base=new SElemType[MAXSIZE];
if(!S.base) exit (OVERFLOW);
S.top=S.base;
S.stacksize=MAXSIZE;
}
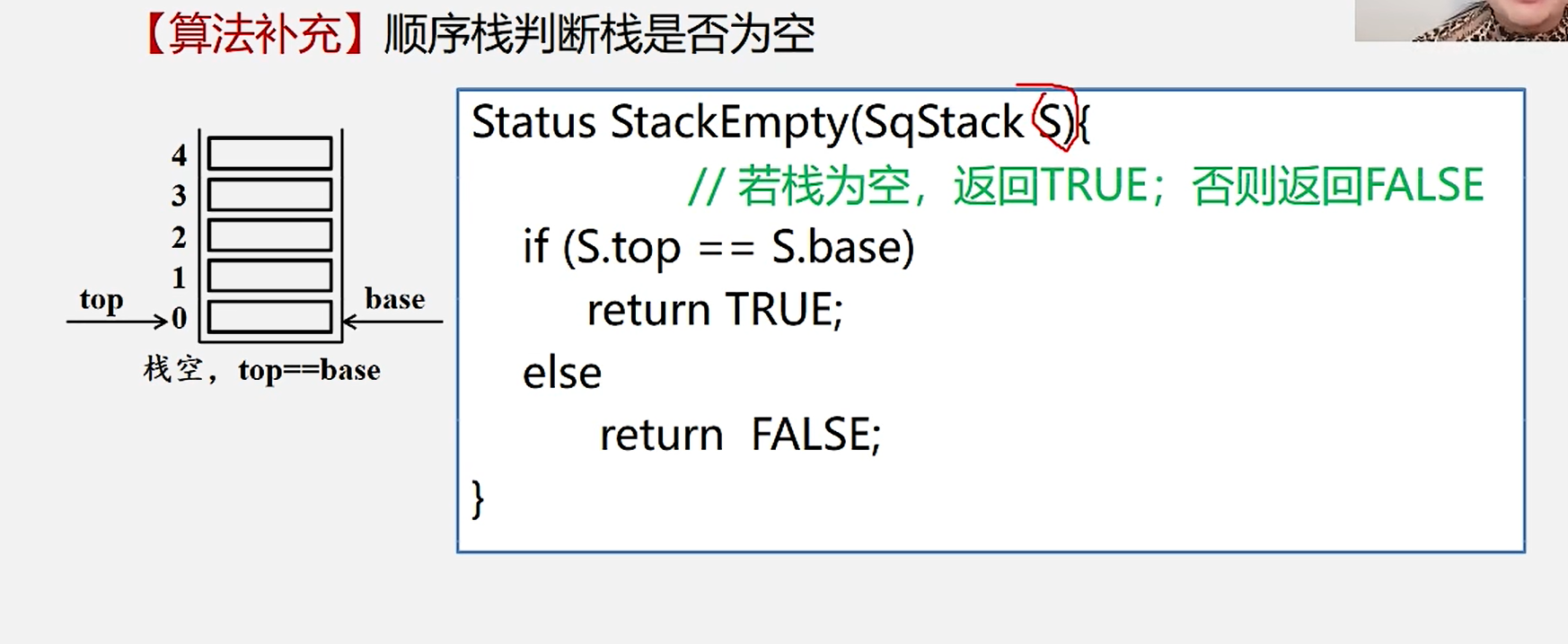
4.判断顺序栈是否为空
Status StackEmpty(SqStack S){
if(S.top==S.base)
return TRUE;
else
return FALSE;
}
5.求顺序栈长度
int StackLength(SqStack S){
retrun S.top-S.base;
}

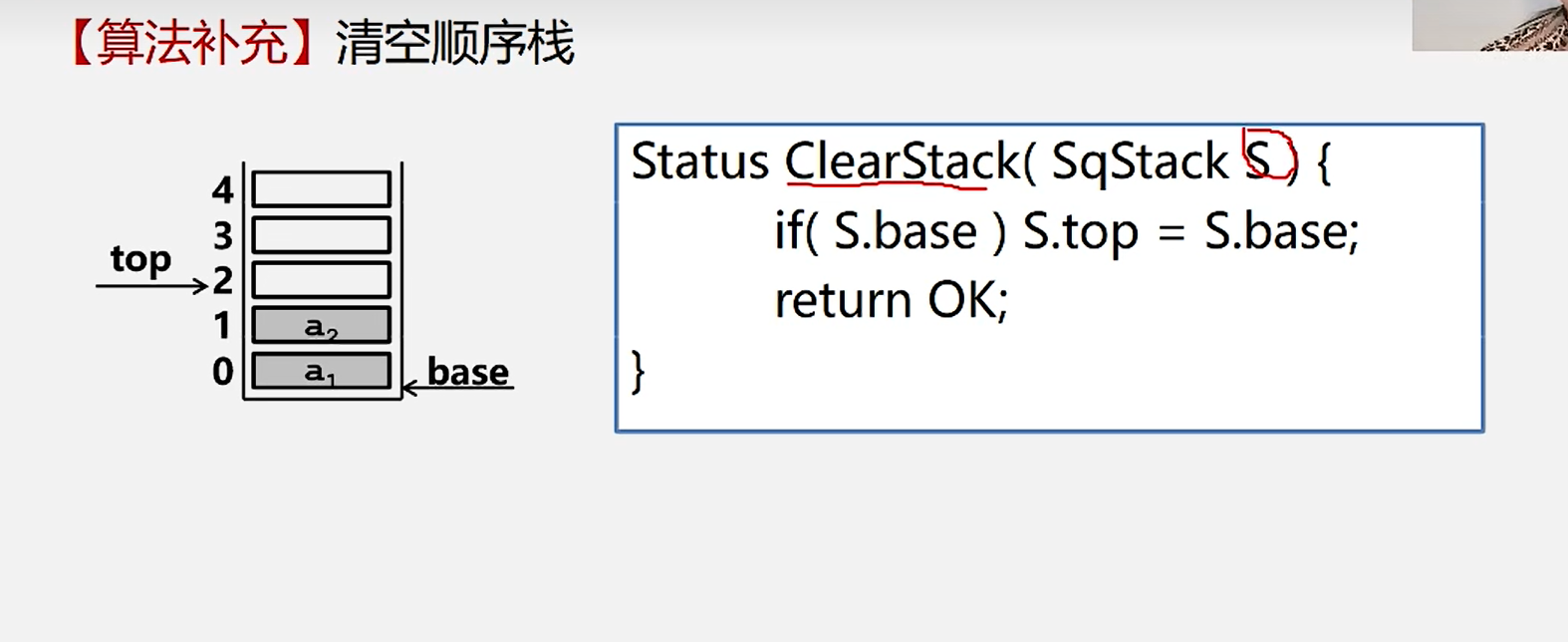
6.清空顺序栈
Status ClearStack(SqStatck S){
if(S.base) S.top=S.base;
return ok;
}
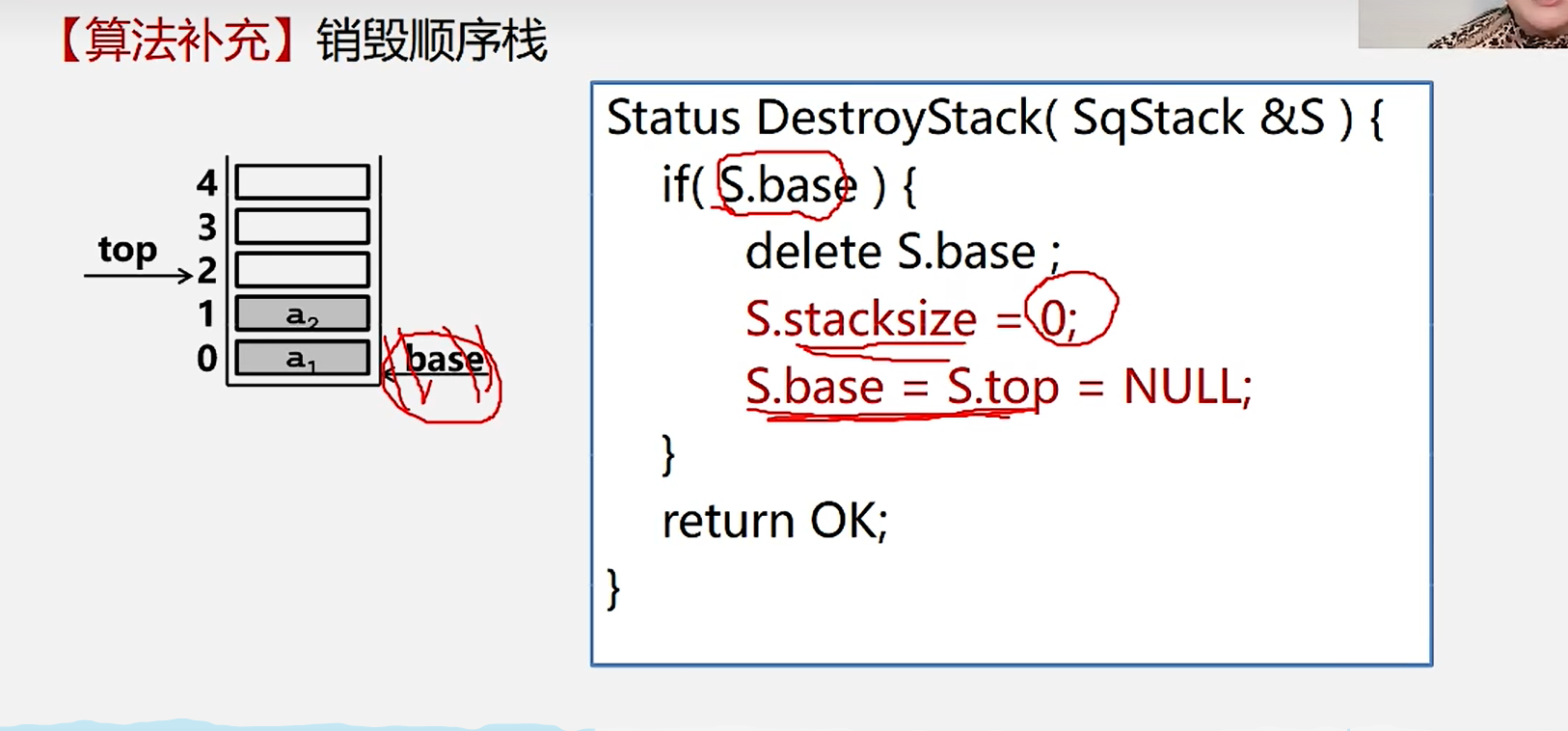
7.销毁顺序栈
Status DestroyStack(SqStack &S){
if(S.base){
delete S.base;
S.stacksize=0;
S.base=S.top=Null;
}
return ok;
}
8.顺序栈的入栈
1.判断是否栈满,若满则出错
2.元素e压入栈顶
3.栈顶指针加1
Status Push(SqStack &S,SElemType e){
if(S.top-S.base==S.stacksize){
return ERROR;
}
*S.top=e; //*S.top是取出S.top指针所指的元素
S.top++; //top指针上移一个位置
return ok;
}

*号的优先级高,++后面运算
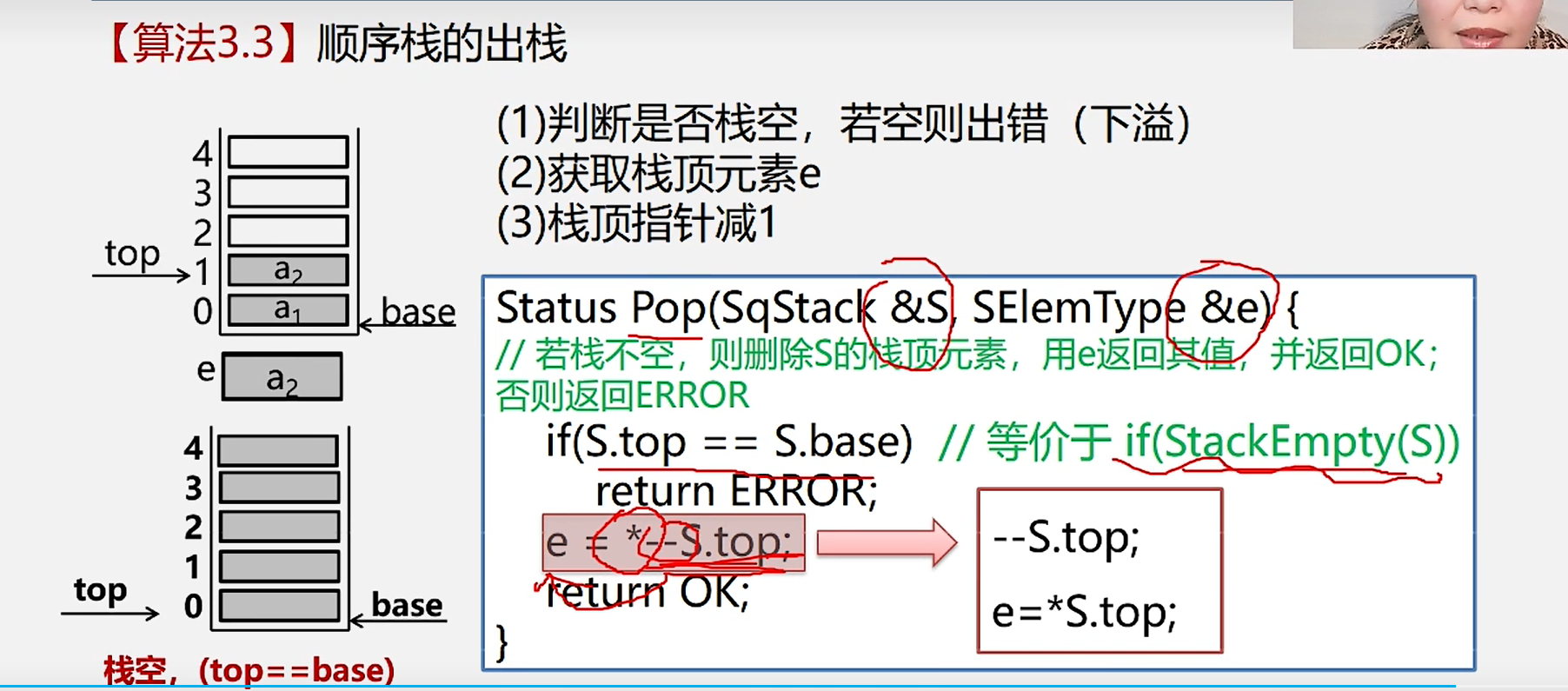
9.顺序栈的出栈
1.判断是否栈空,若空栈则出错(下溢)
2.获取栈顶元素e
3.栈顶指针减1
Status Pop(SqStack &S, SElemType &e){
if(S.top==S.base){
retrun Error;
}
--S.top;
e=S.top;
return ok;
}
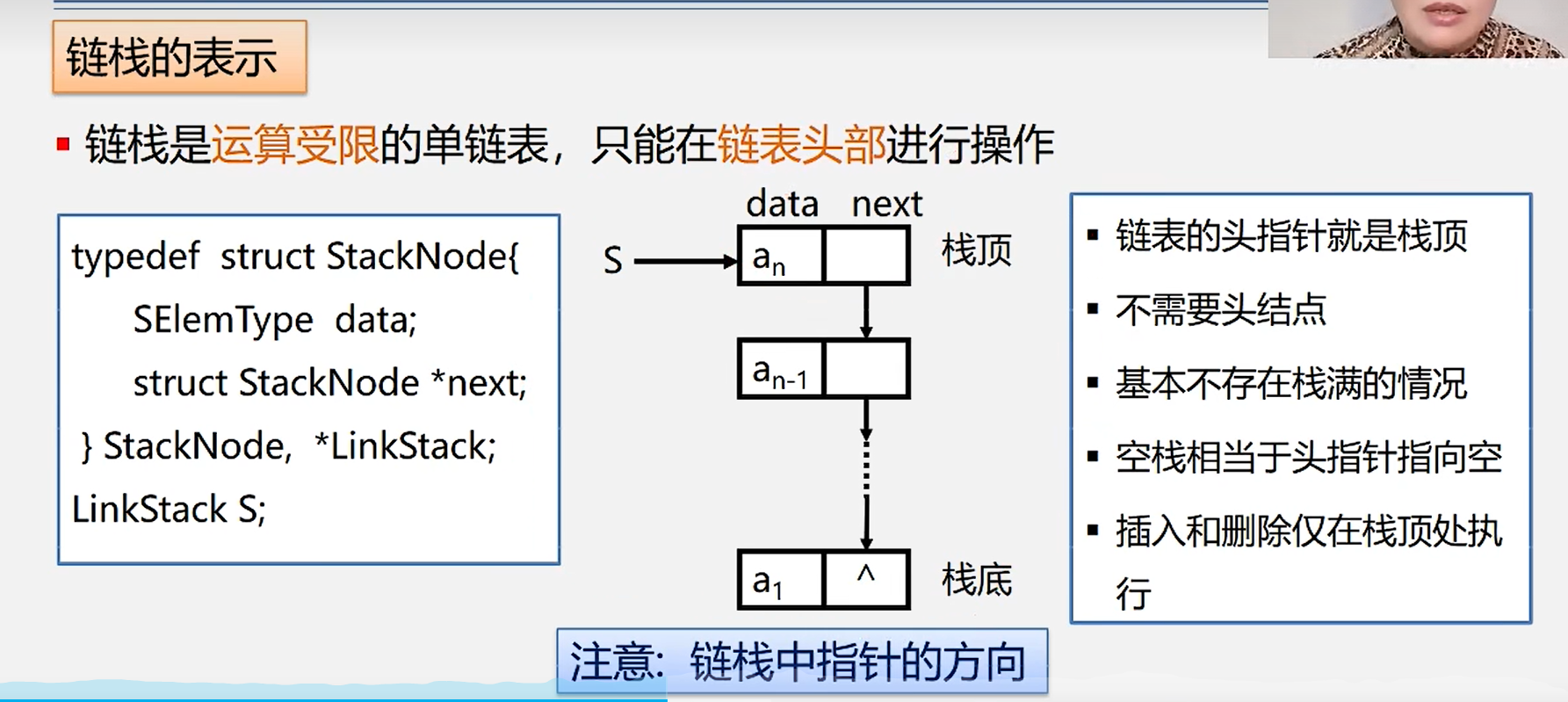
4.链栈
1.链栈的表示
typedef struct StackNode{
SElemType data;
struct StackNode *next;
}StackNode, *LinkStack;
LinkStack S;
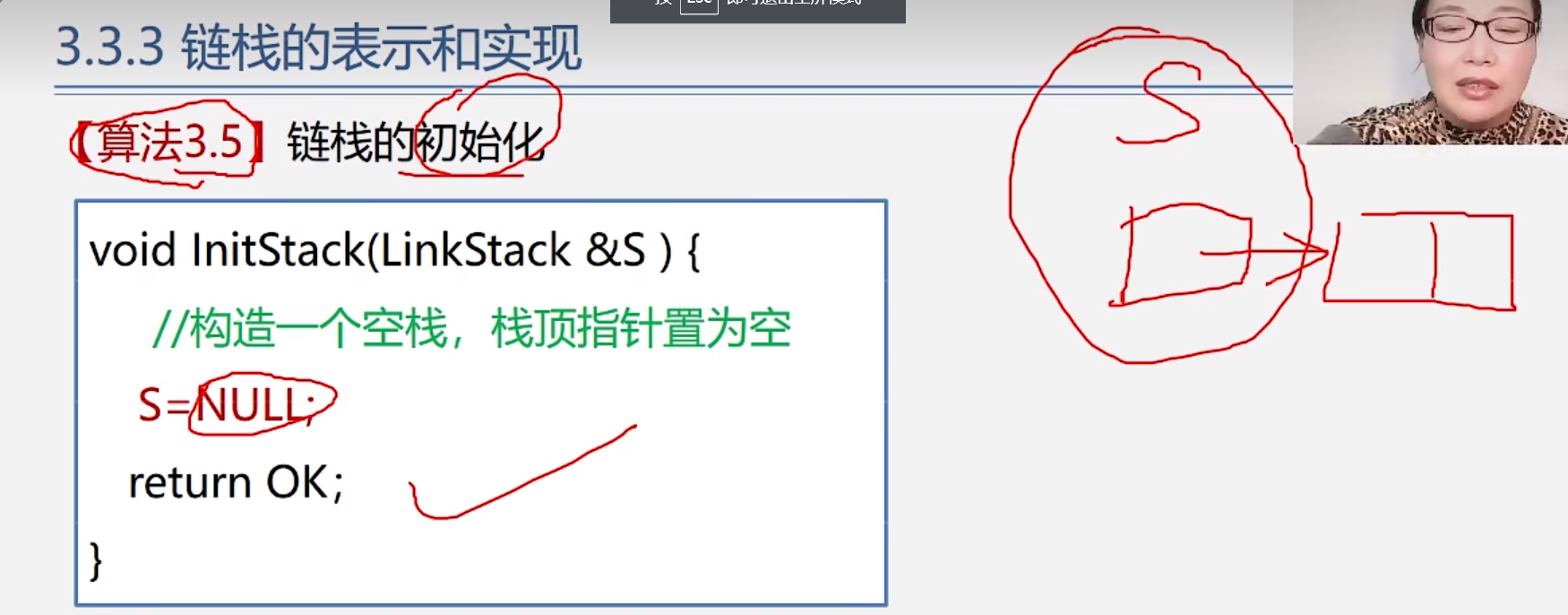
2.链栈的初始化
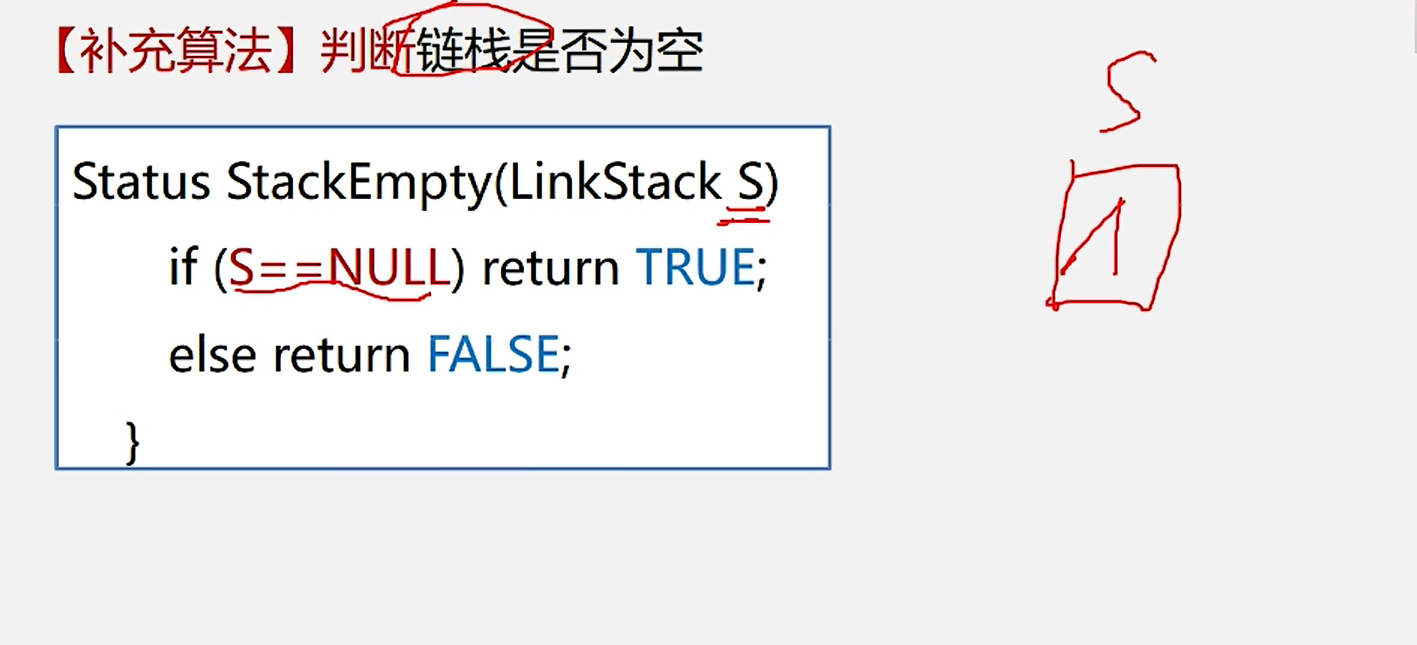
3.判断链栈是否为空
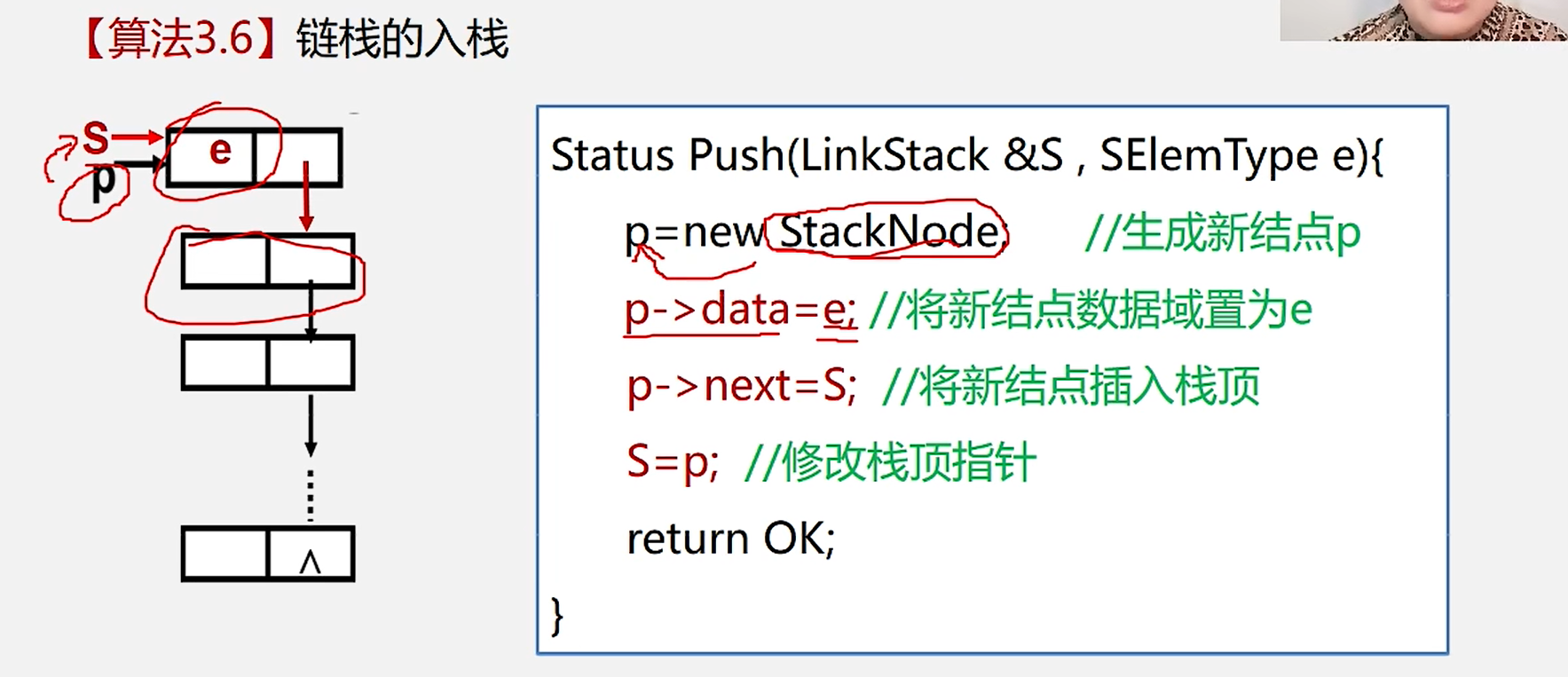
4.链栈入栈
5.链栈的出栈
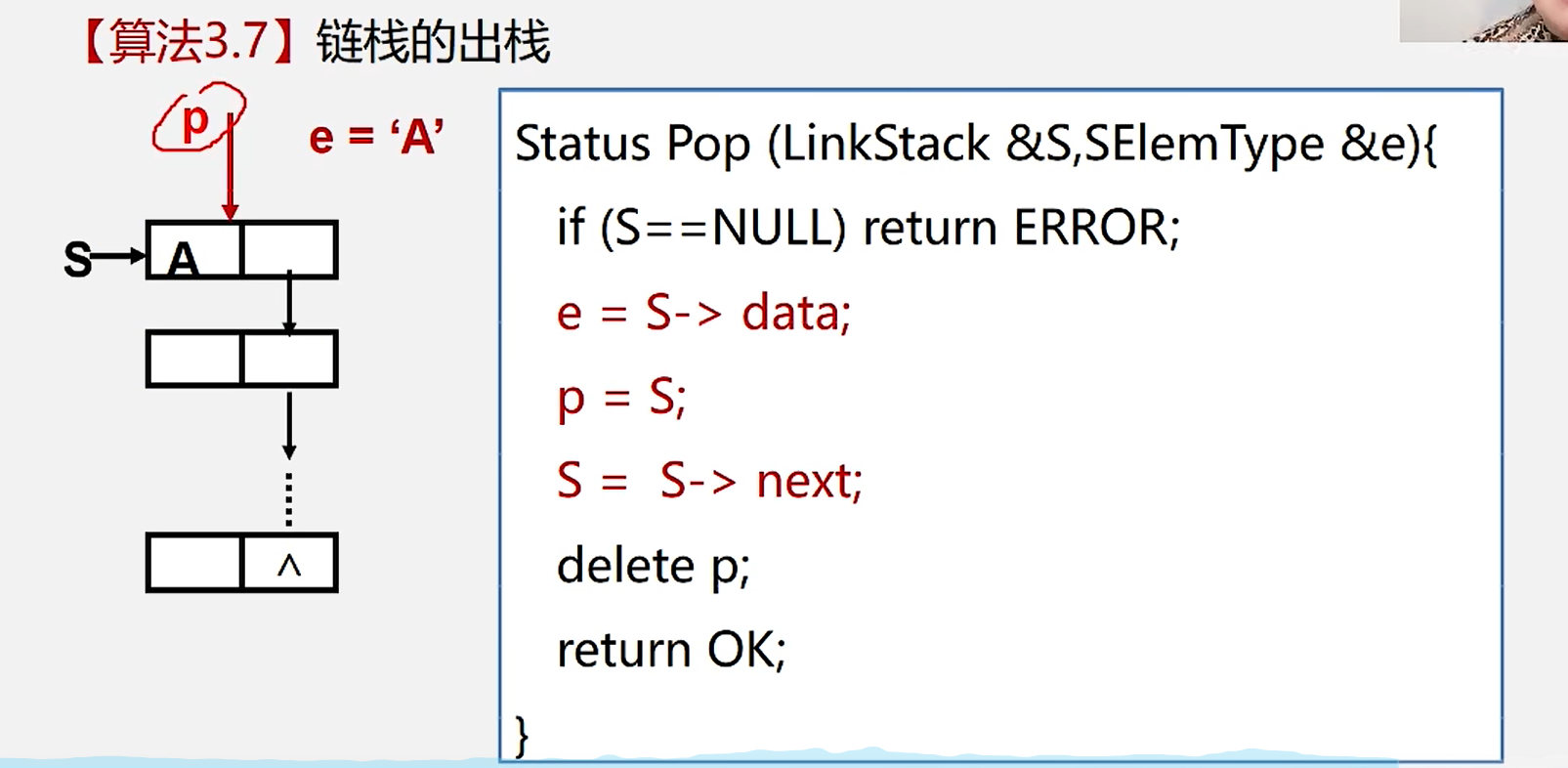
6.取栈顶元素
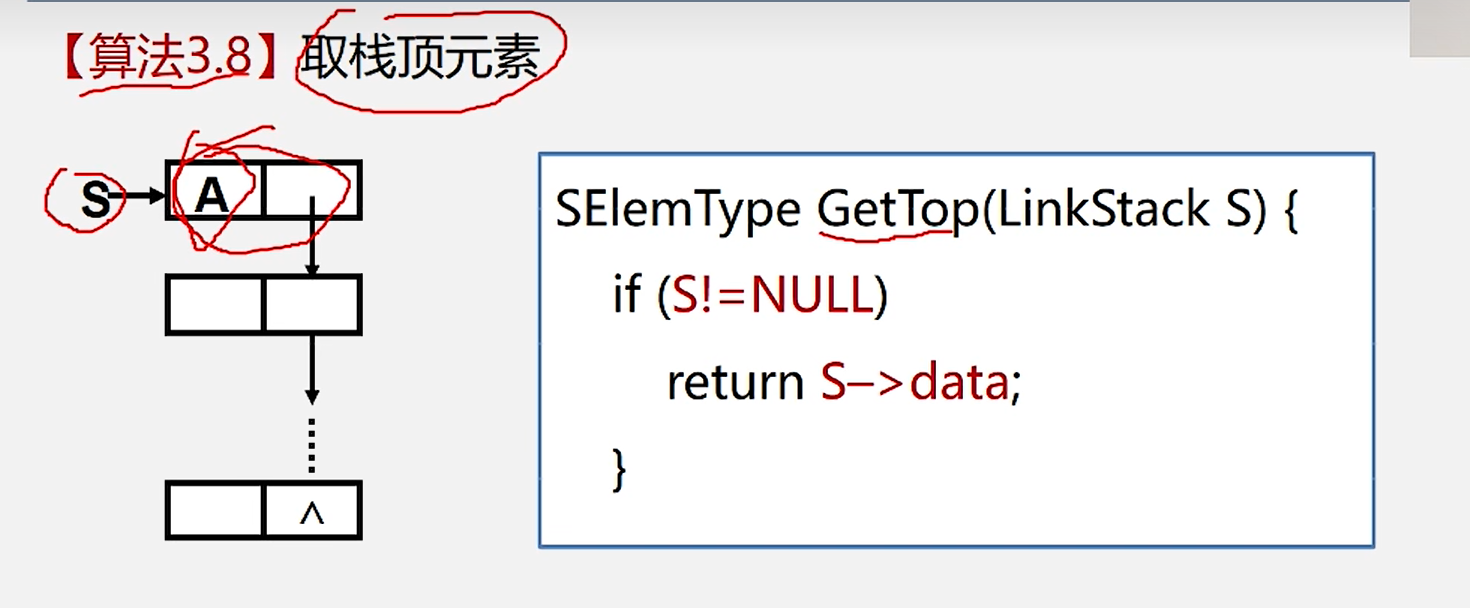
6.栈与递归
1.递归的定义

2.递归的三种应用场景
1.递归定义的数学函数

2.具有递归特性的数据结构
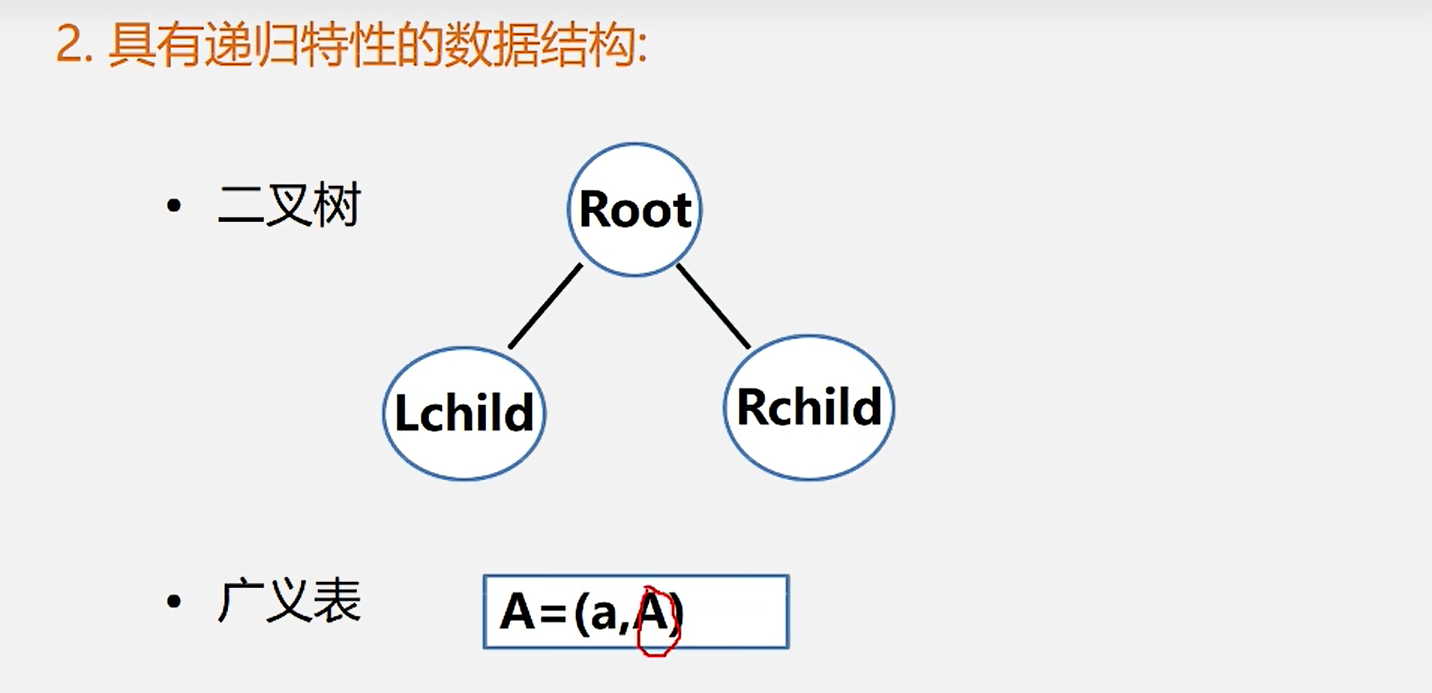
3.可递归求解的问题
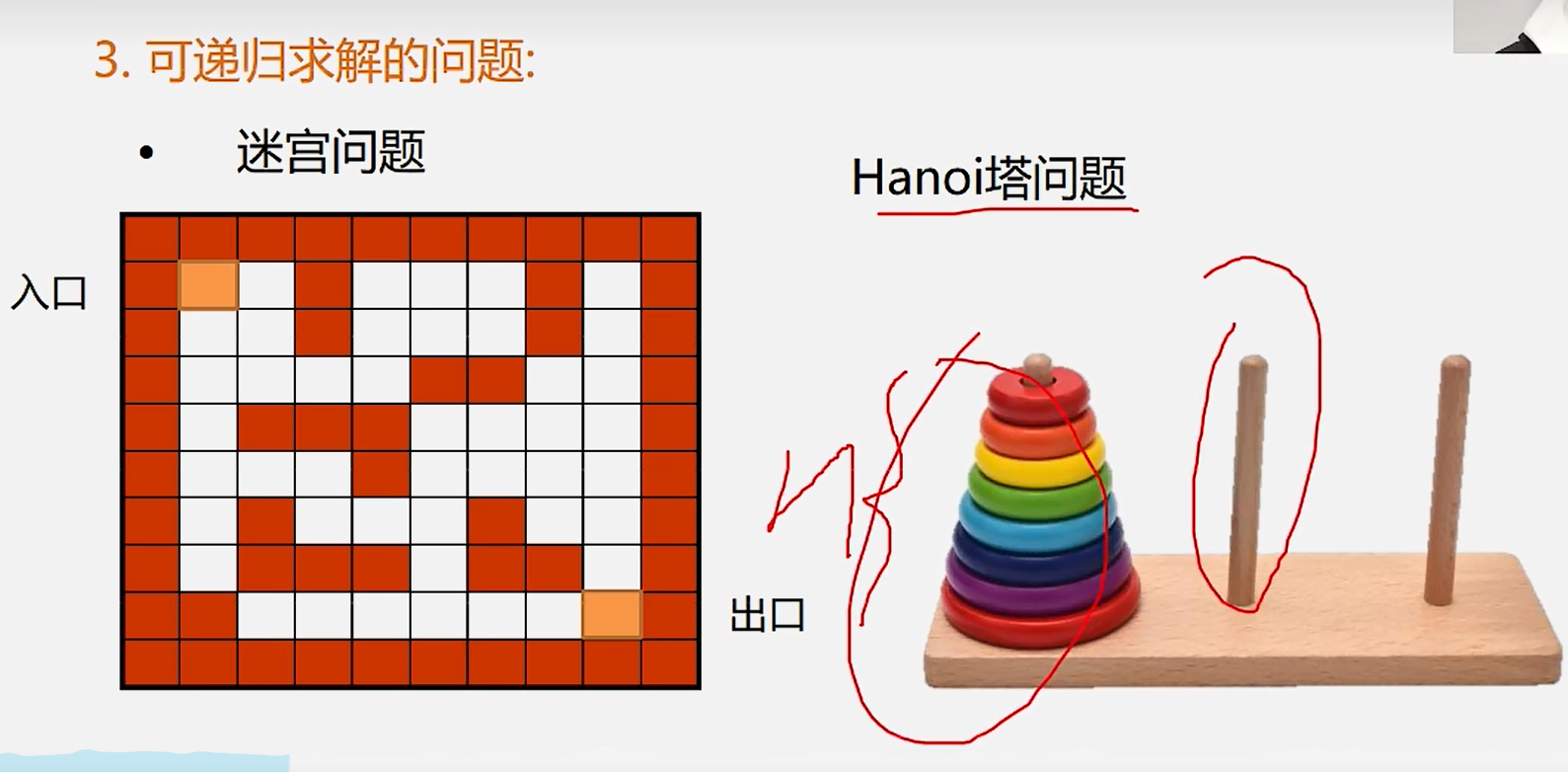
3.递归问题
1.递归是分治法的一种
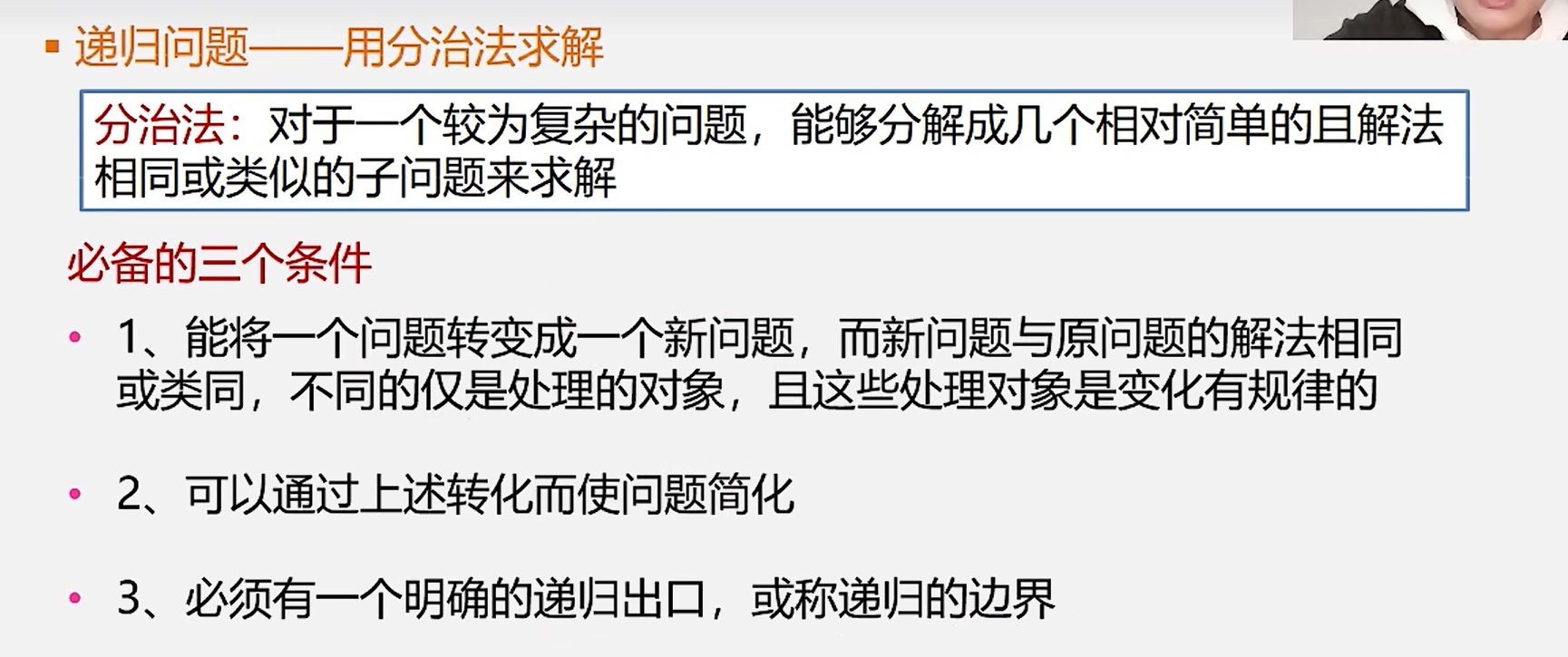
2.递归算法的一般形式
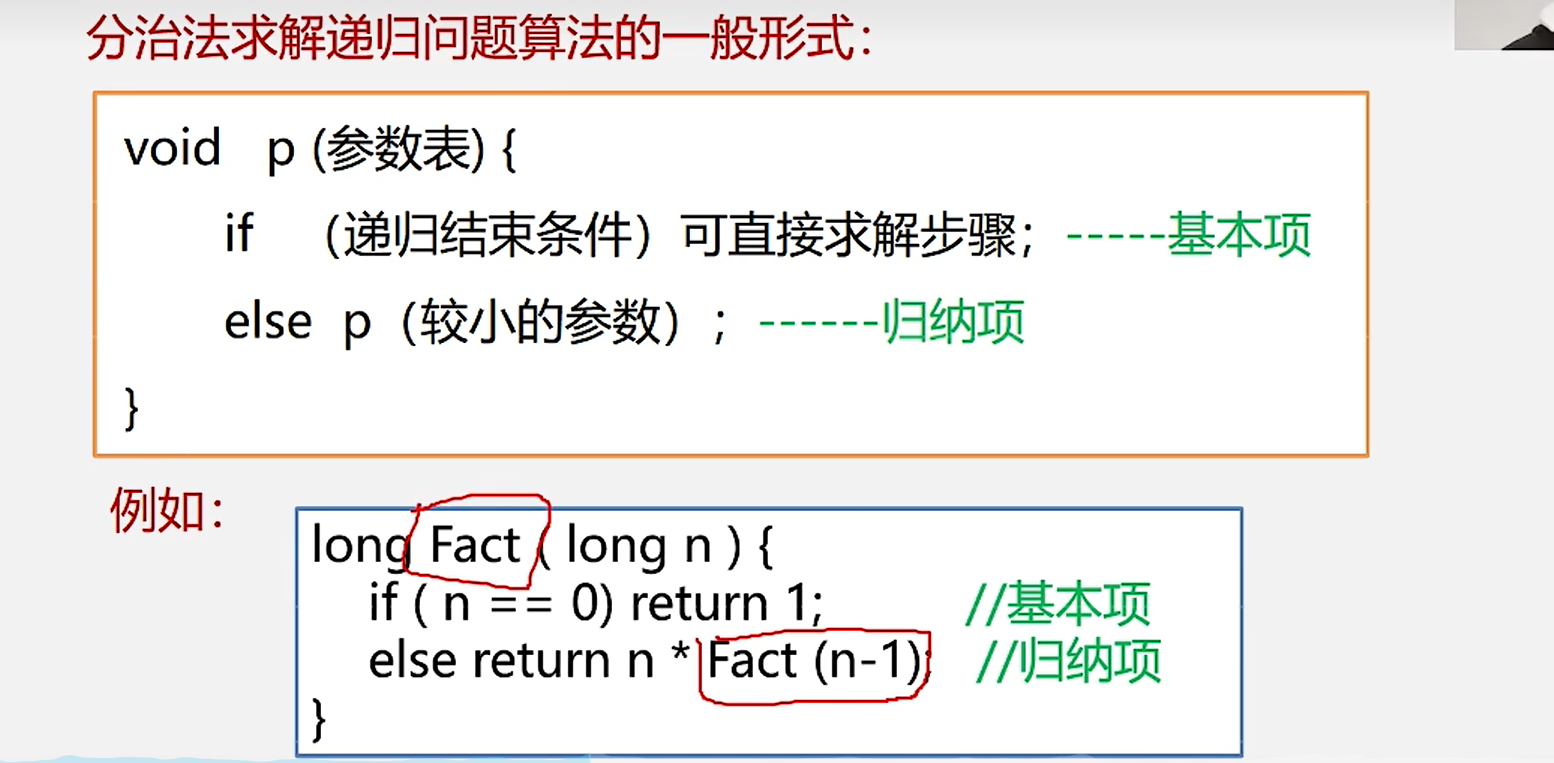
3.函数调用过程

4.多个函数构成嵌套调用
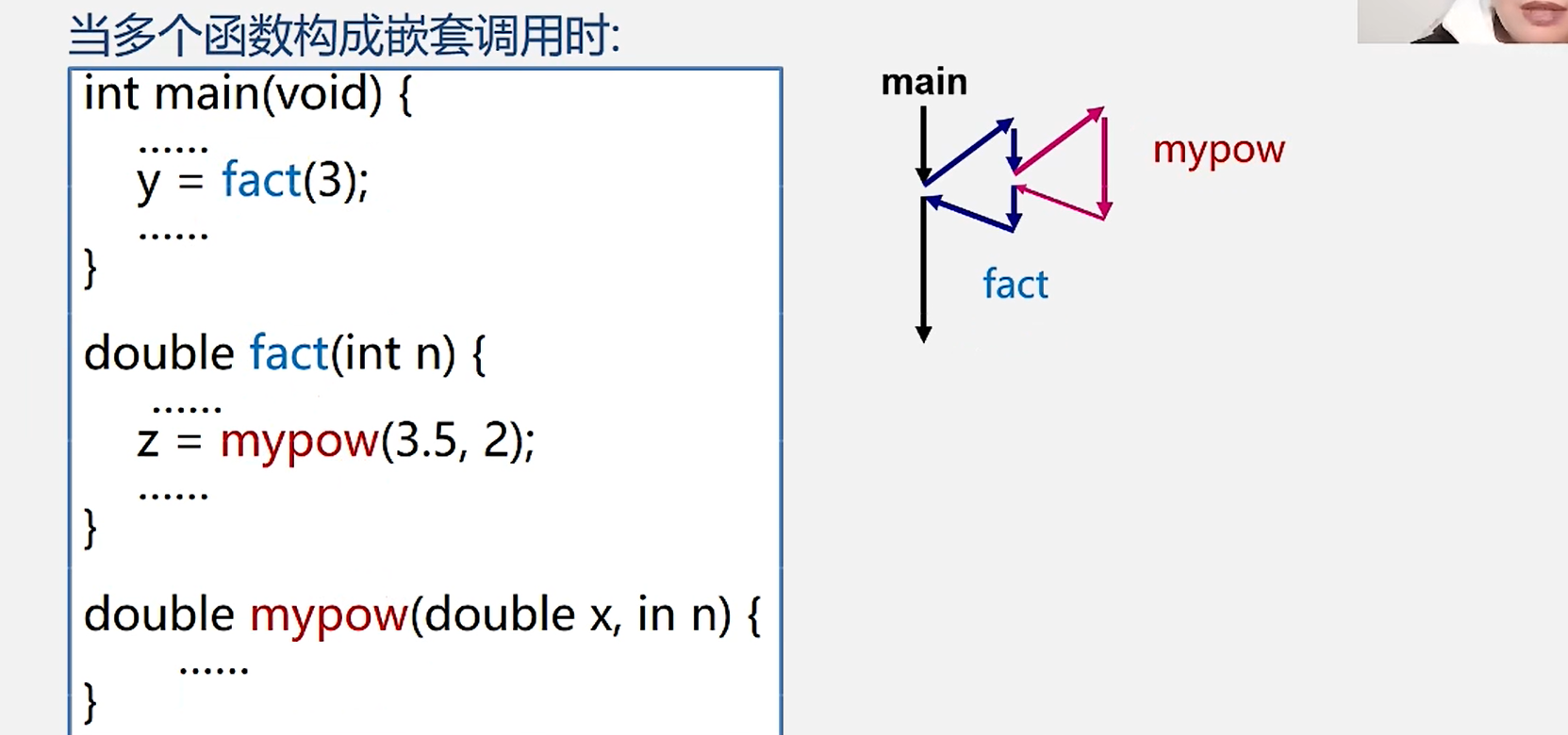
1.求n!过程
if(n==0) return 1
else return n*Fact(n-1)

2.递归函数调用的实现
递归工作栈记录:实参,局部变量,返回地址
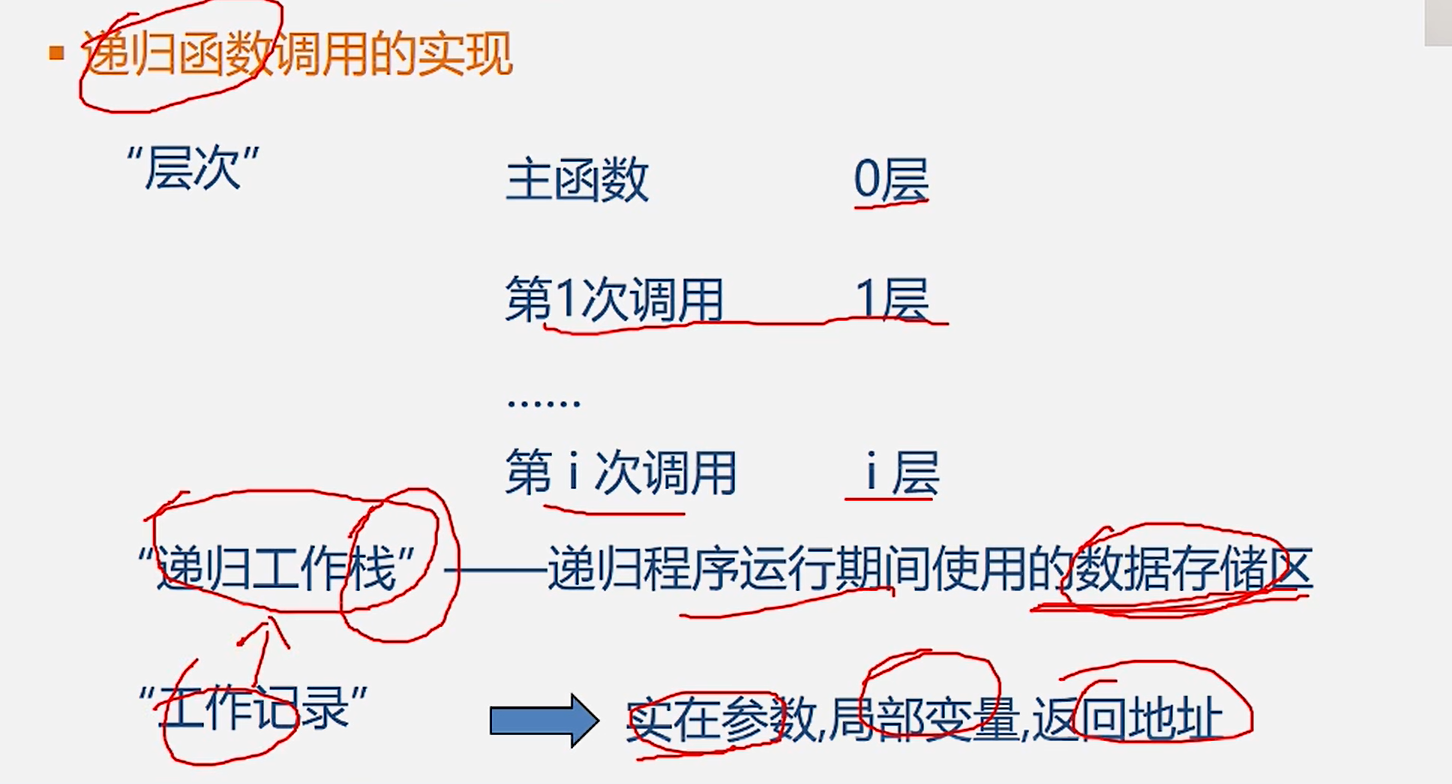
3.系统栈
先押栈,押满后在弹出,结果返回到地址
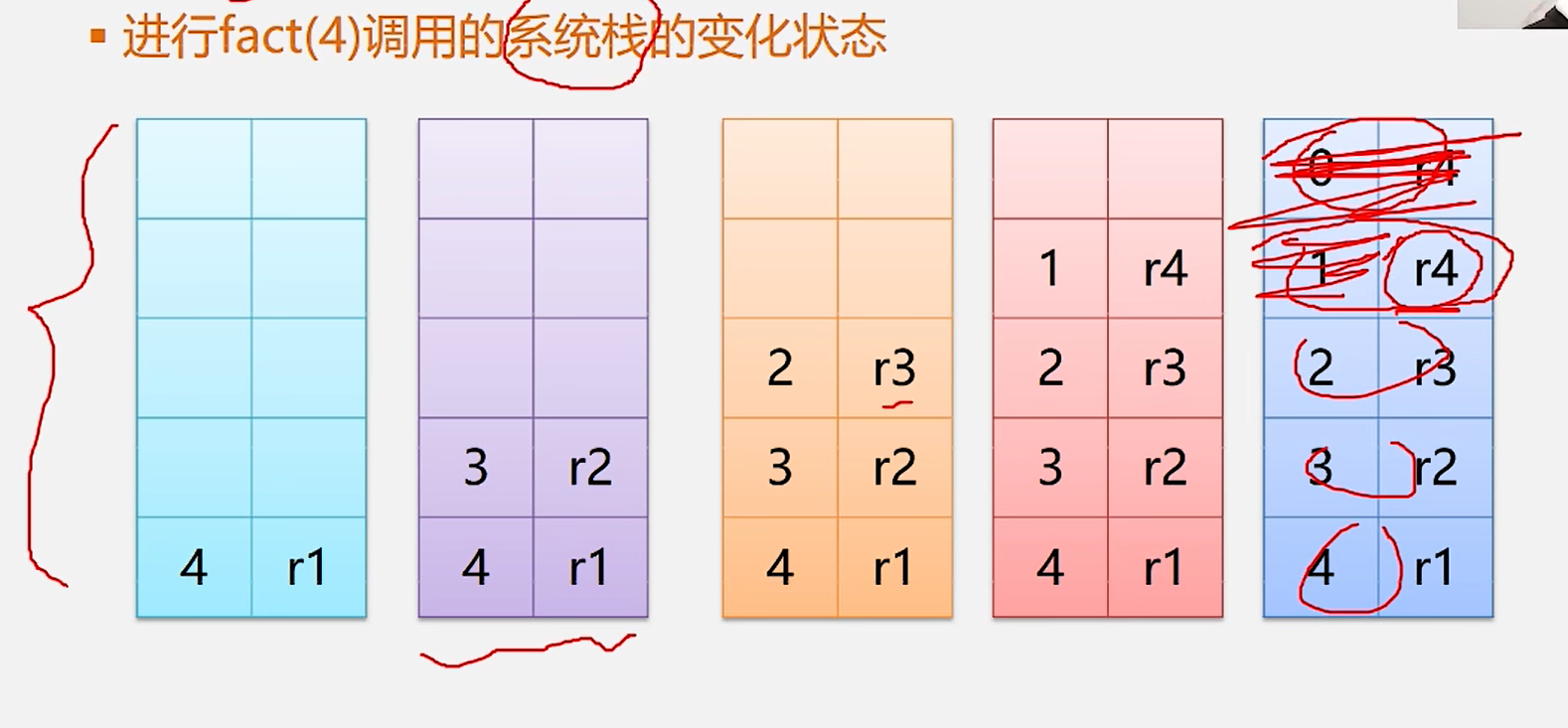
4.递归优缺点:
优点:结构清晰,程序易读
缺点:时间开销大
保存状态信息,入栈。
返回是要出栈,恢复状态信息。
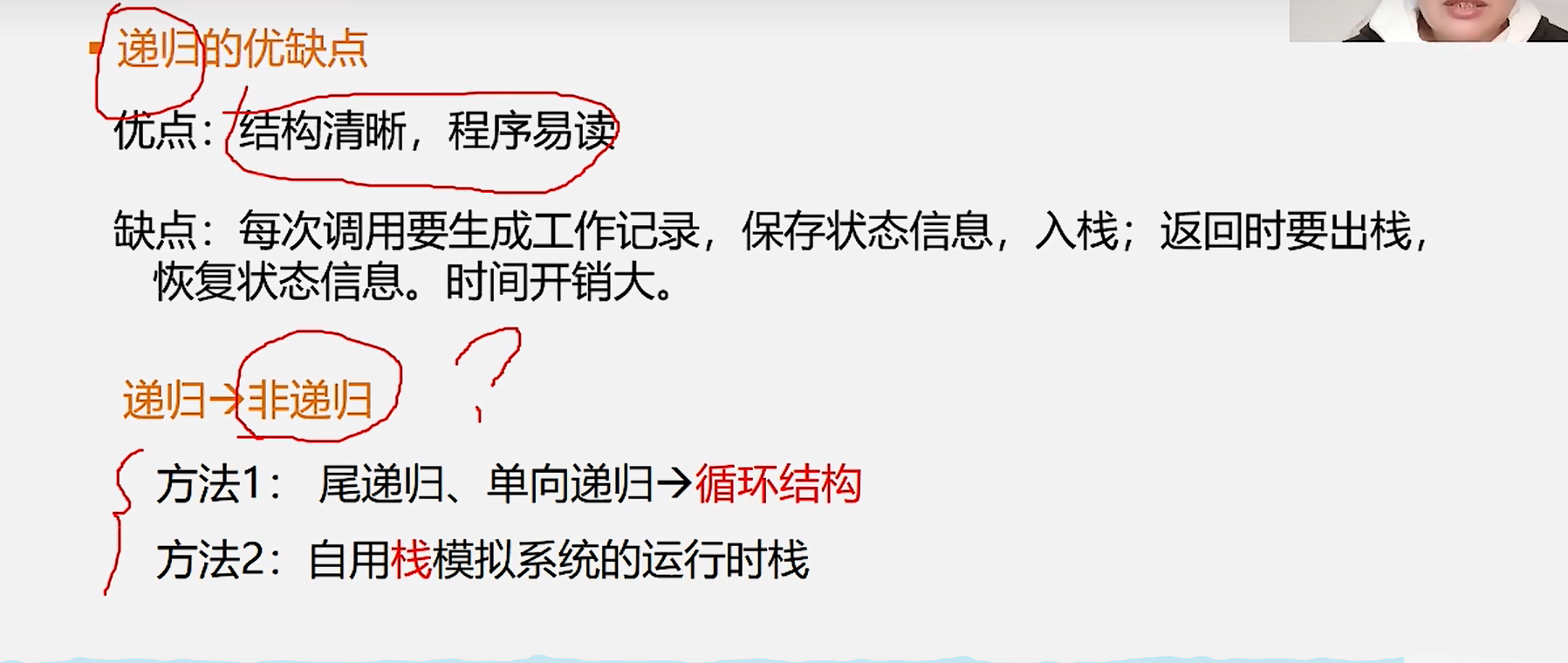
尾递归-》循环递归
long Fact(long n){
t=1;
for(i=1;i<=n;i++) t=t*i;
return t;
}

单向递归-》循环结构
Long Fib(long n){
if(n==1 || n==2) return 1;
else{
t1=1;t2=1;
for(i=3;i<=n;i++){
t3=t1+t2;
t1=t2;t2=t3;
}
return t3;
}
}



7.队列的表示和操作实现
1.回顾
头删,尾插
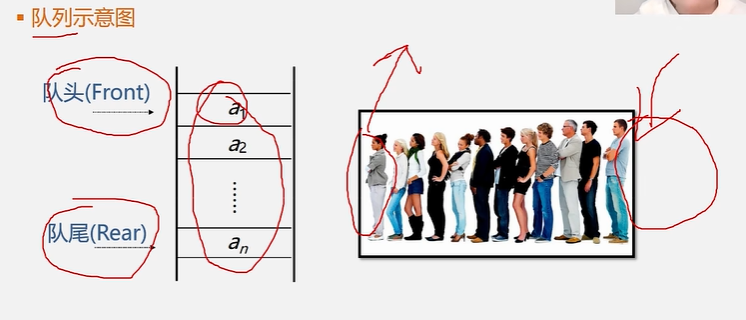
2.相关术语
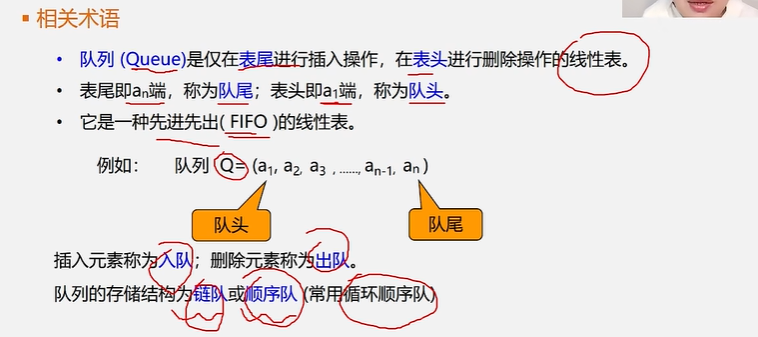
3.队列的相关概念

4.队列的常见应用

2.队列的抽象数据类型定义

1.顺序队列表示和实现

2.顺序表的操作
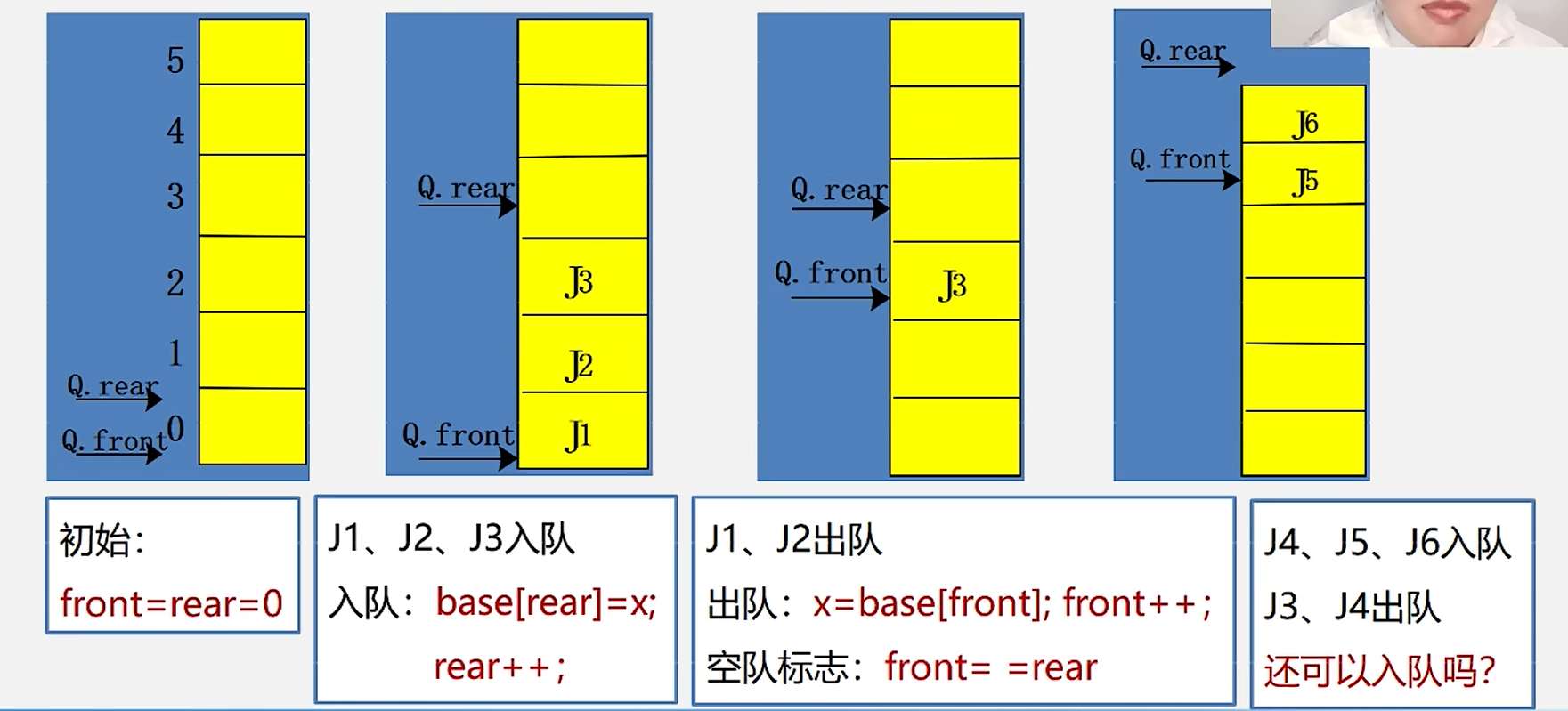
1.真假溢出
真溢出:front=0 rear=MAXQSIZE
假溢出:front!=0 rear=MAXQSIZE

2.解决假溢出的方法
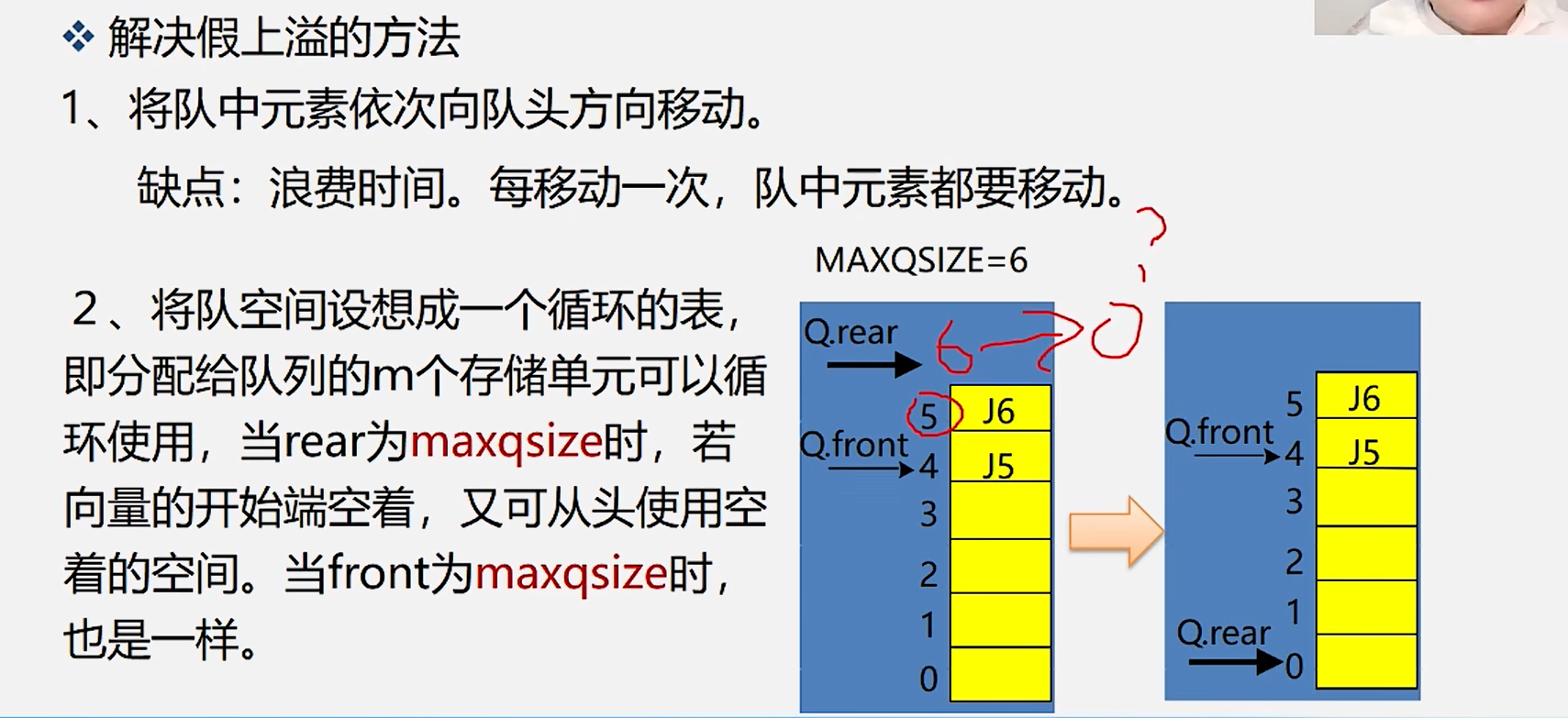
3.引入循环队列

4.解决如何区别队空和队满相等的情况
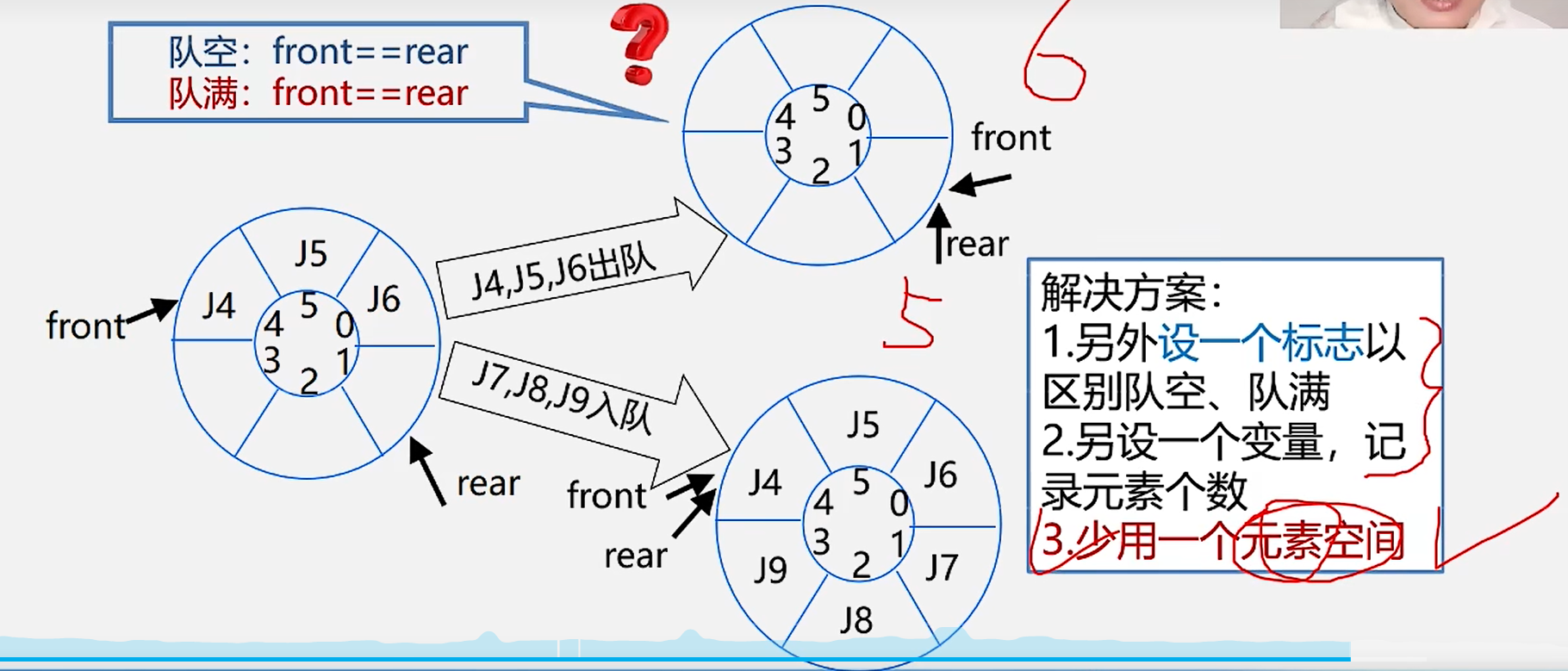
5.少用一个元素空间
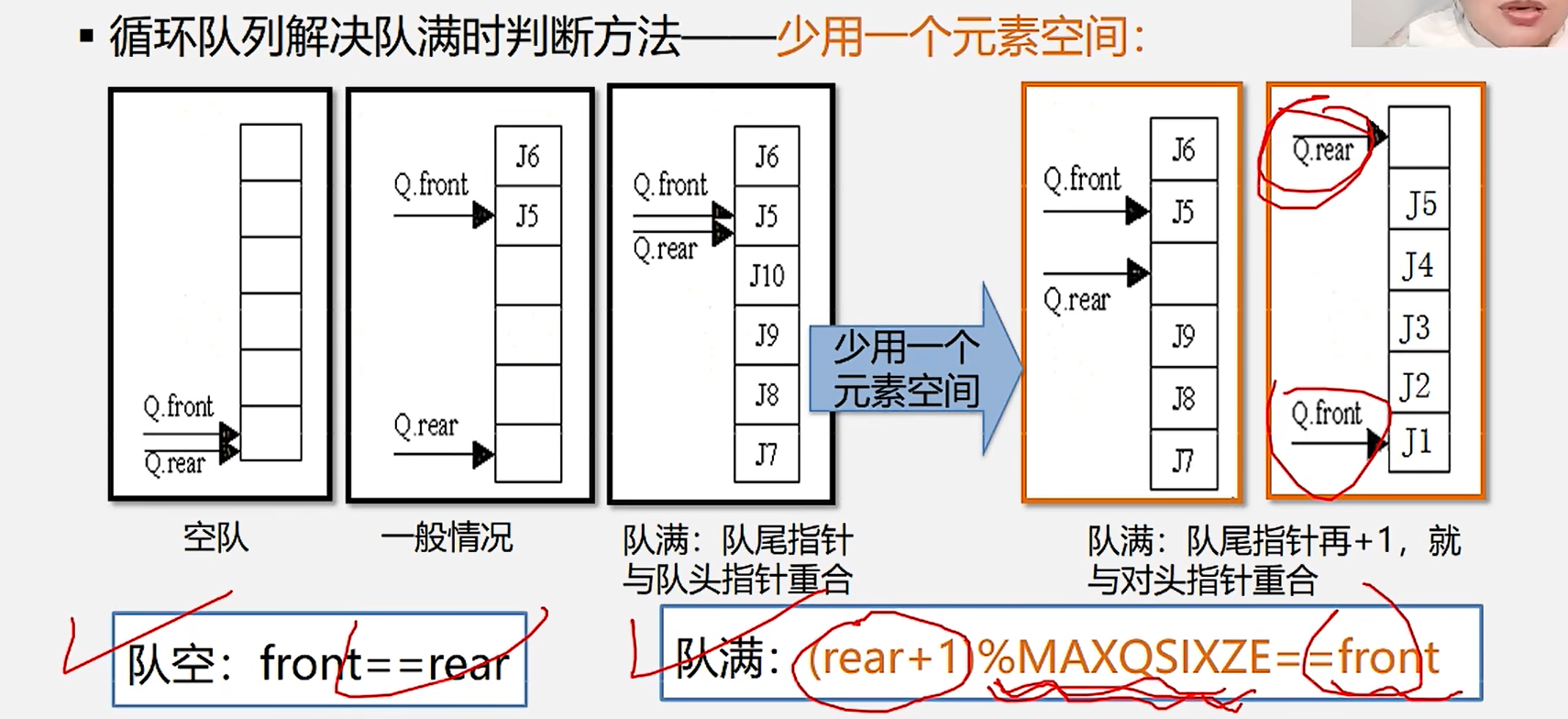
6.求队列的长度
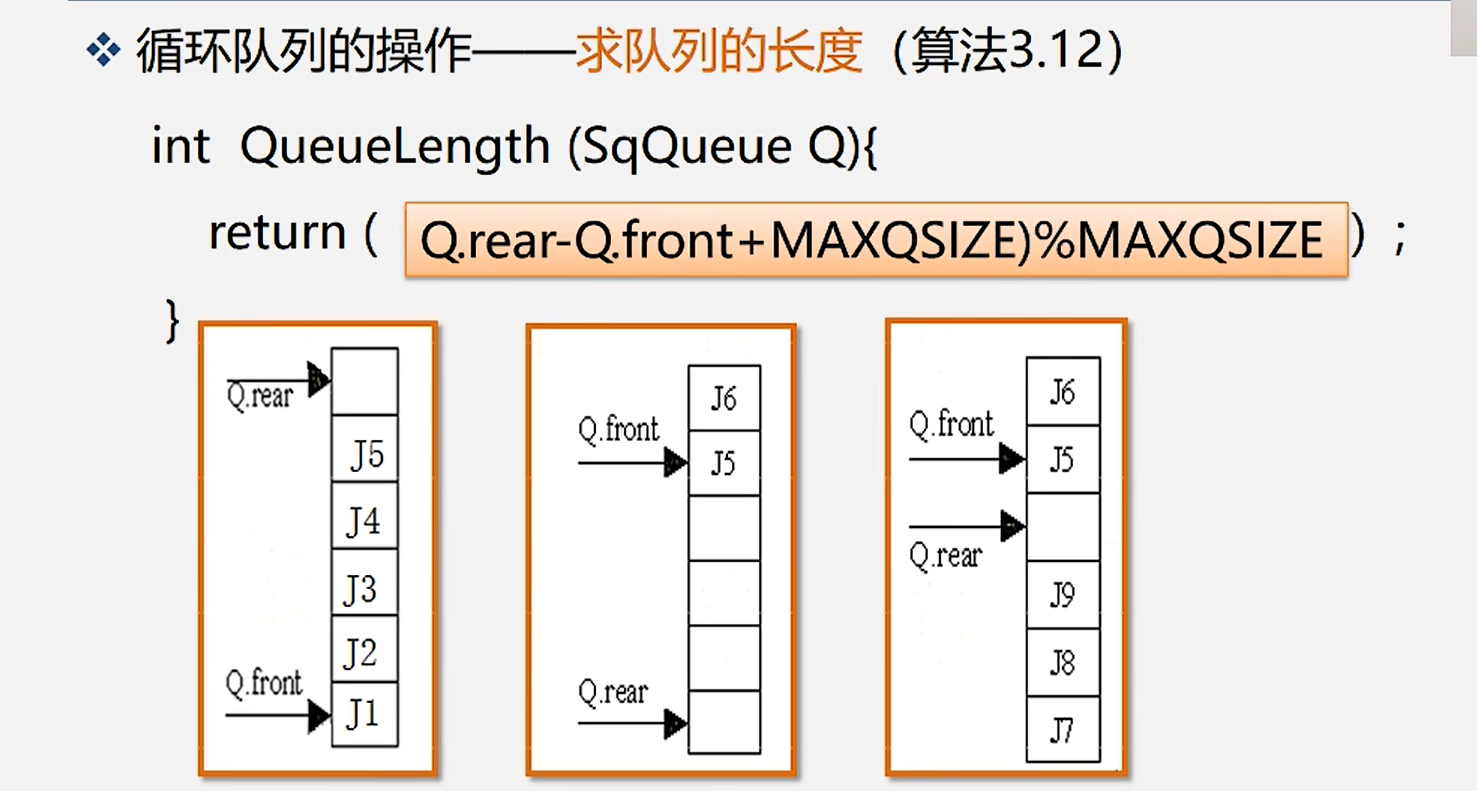

7.循环队列入队
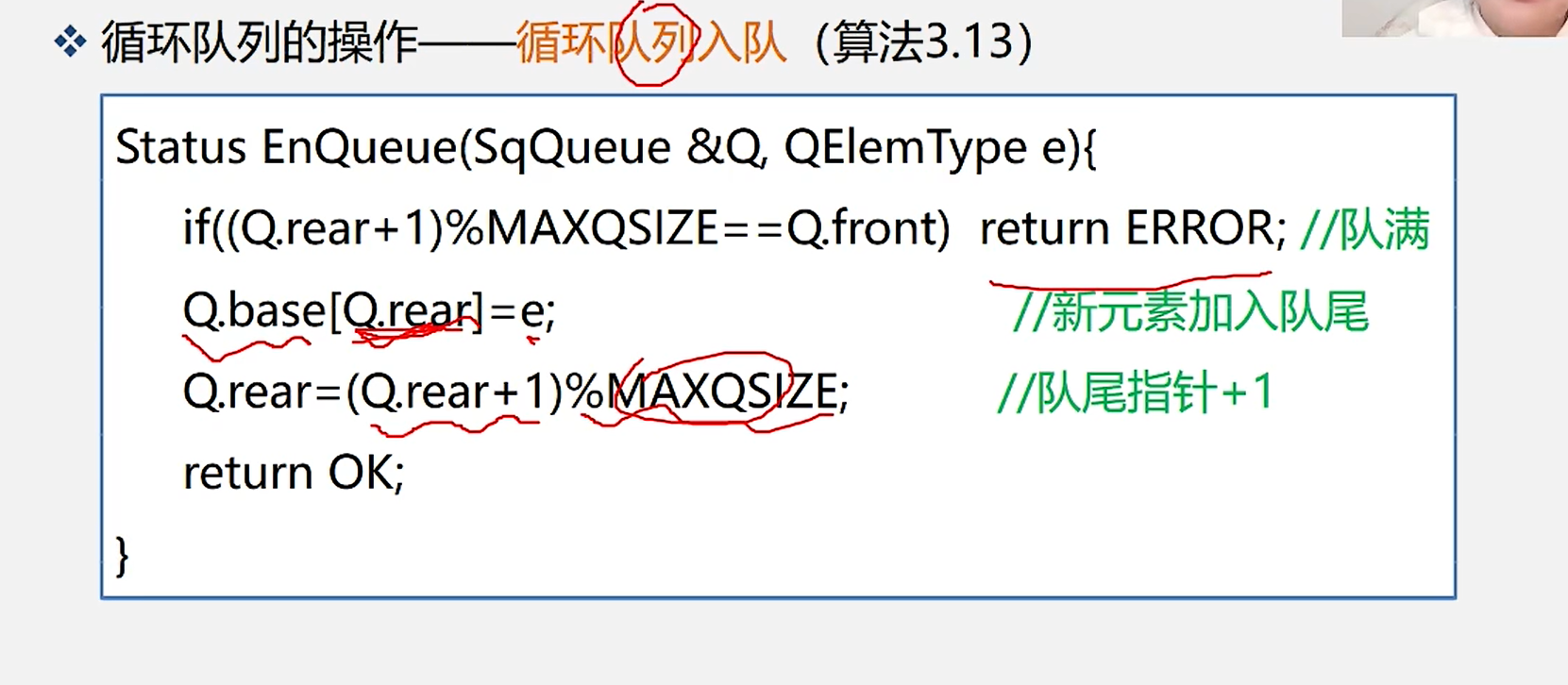
8.循环队列出队
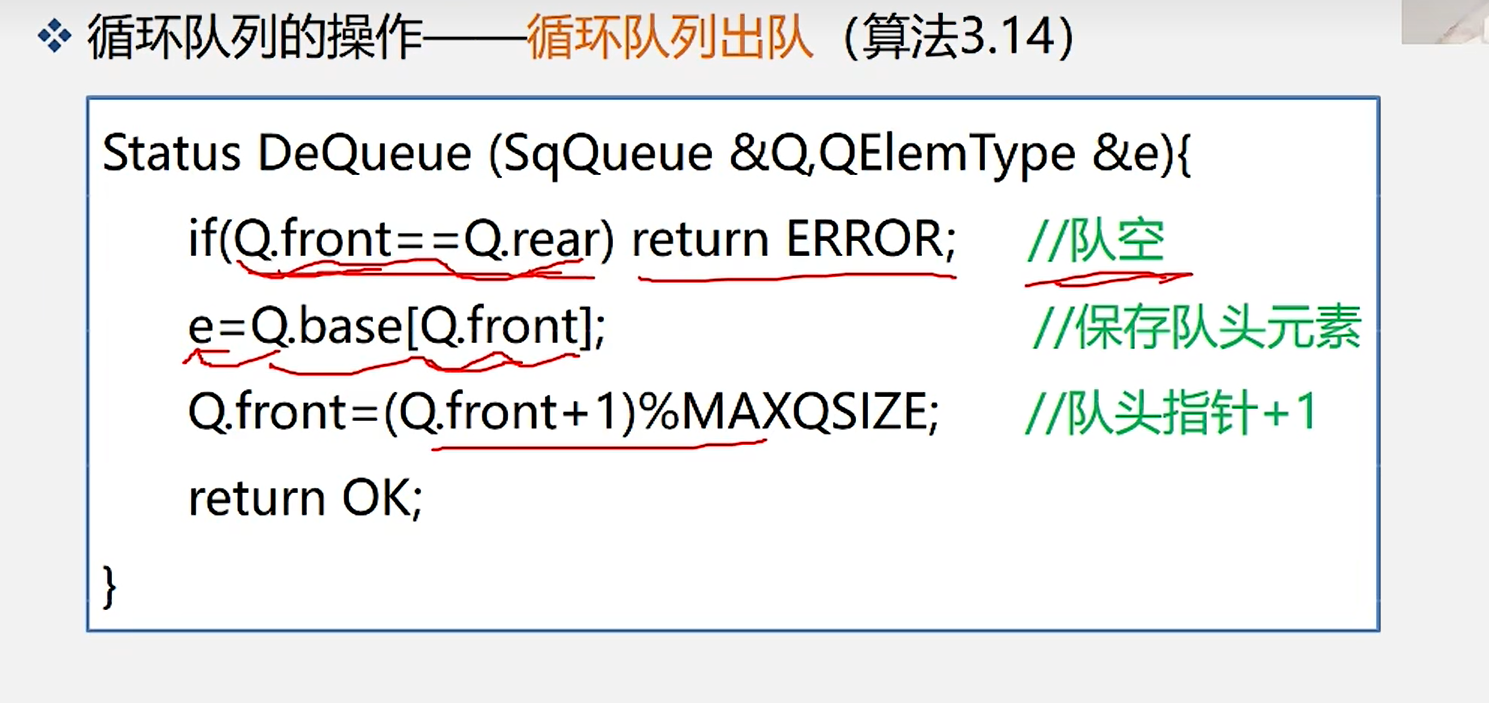
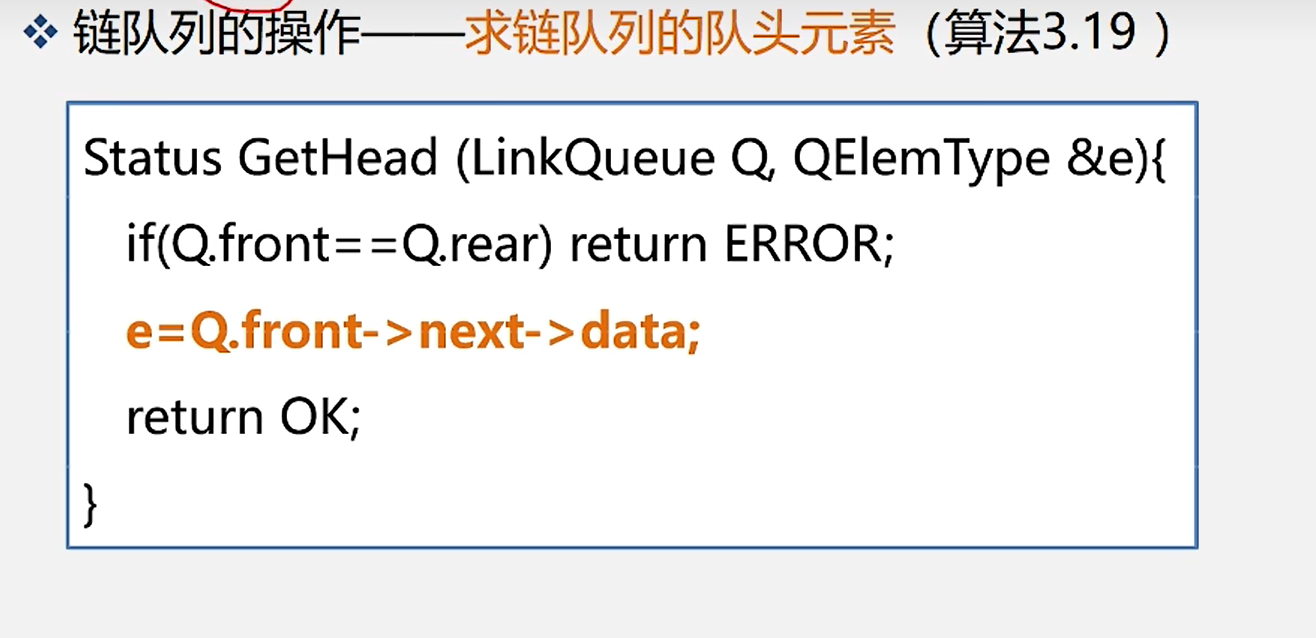
9.取队头元素
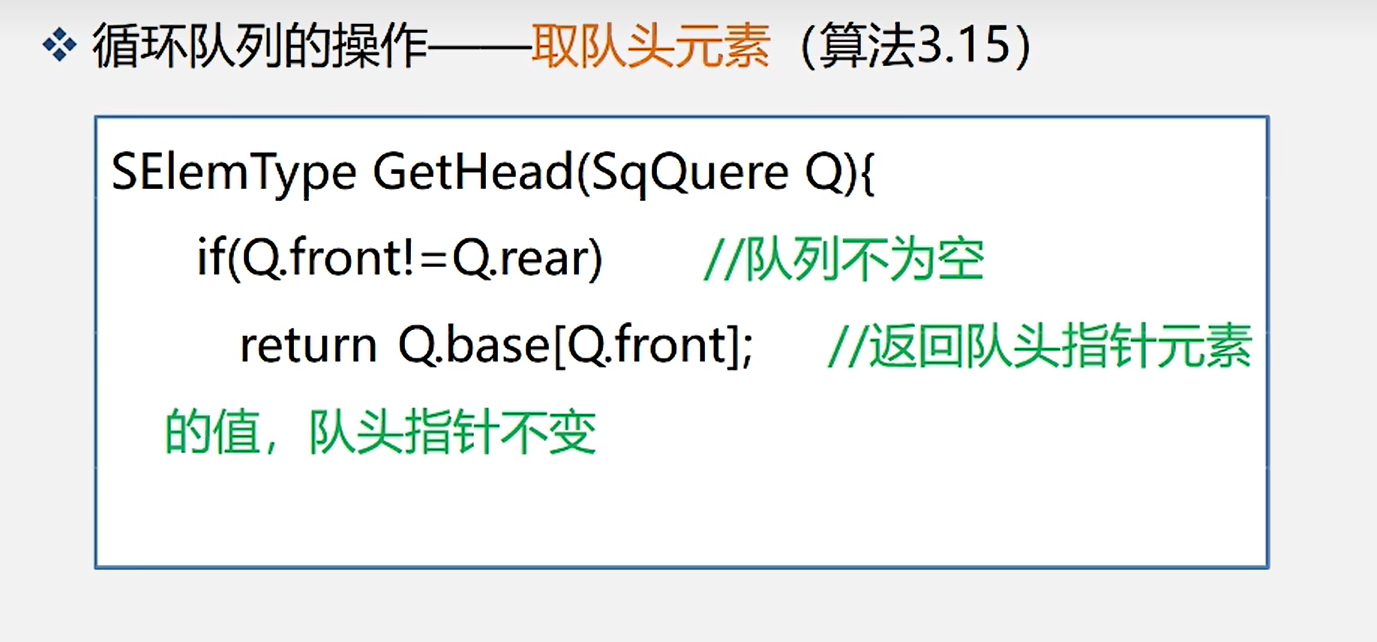
3.队列链表的操作与实现
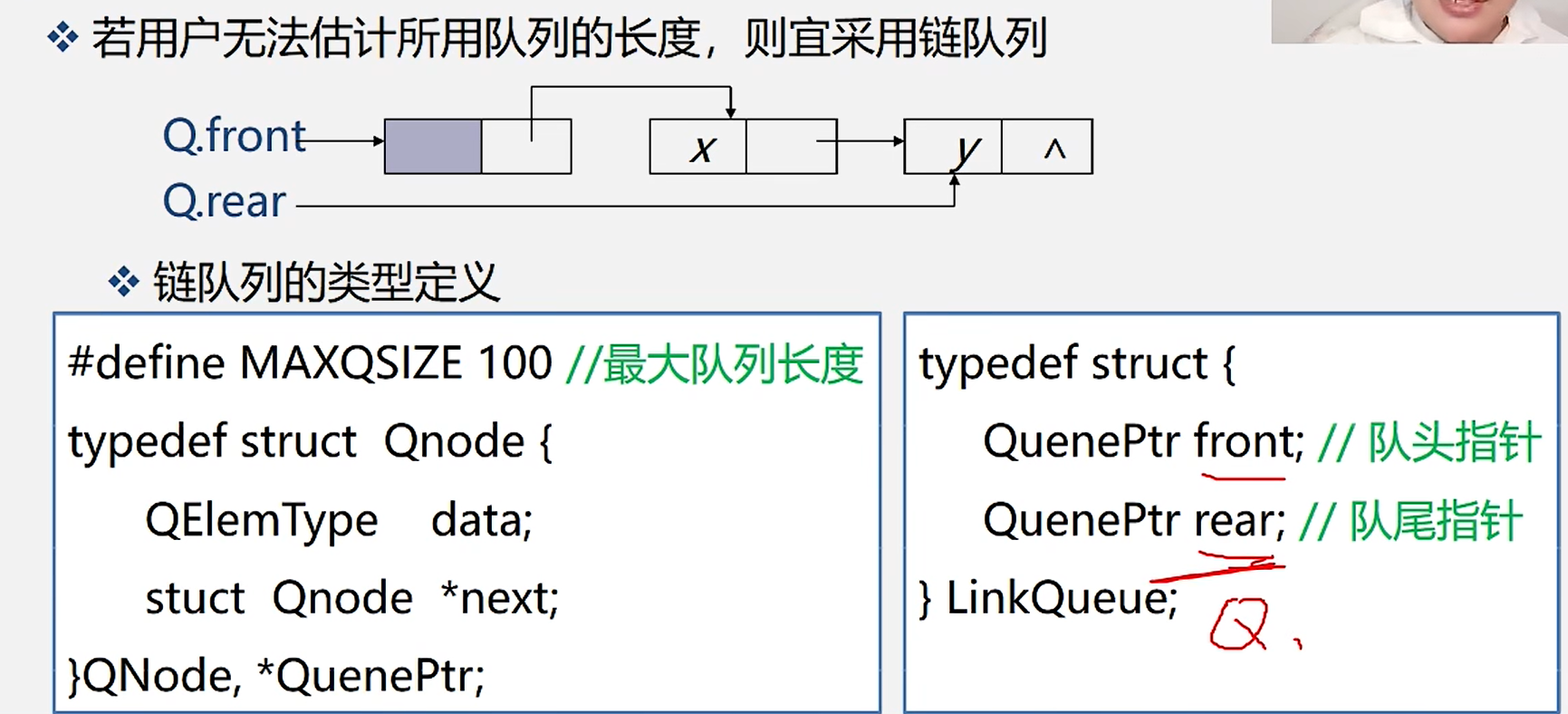
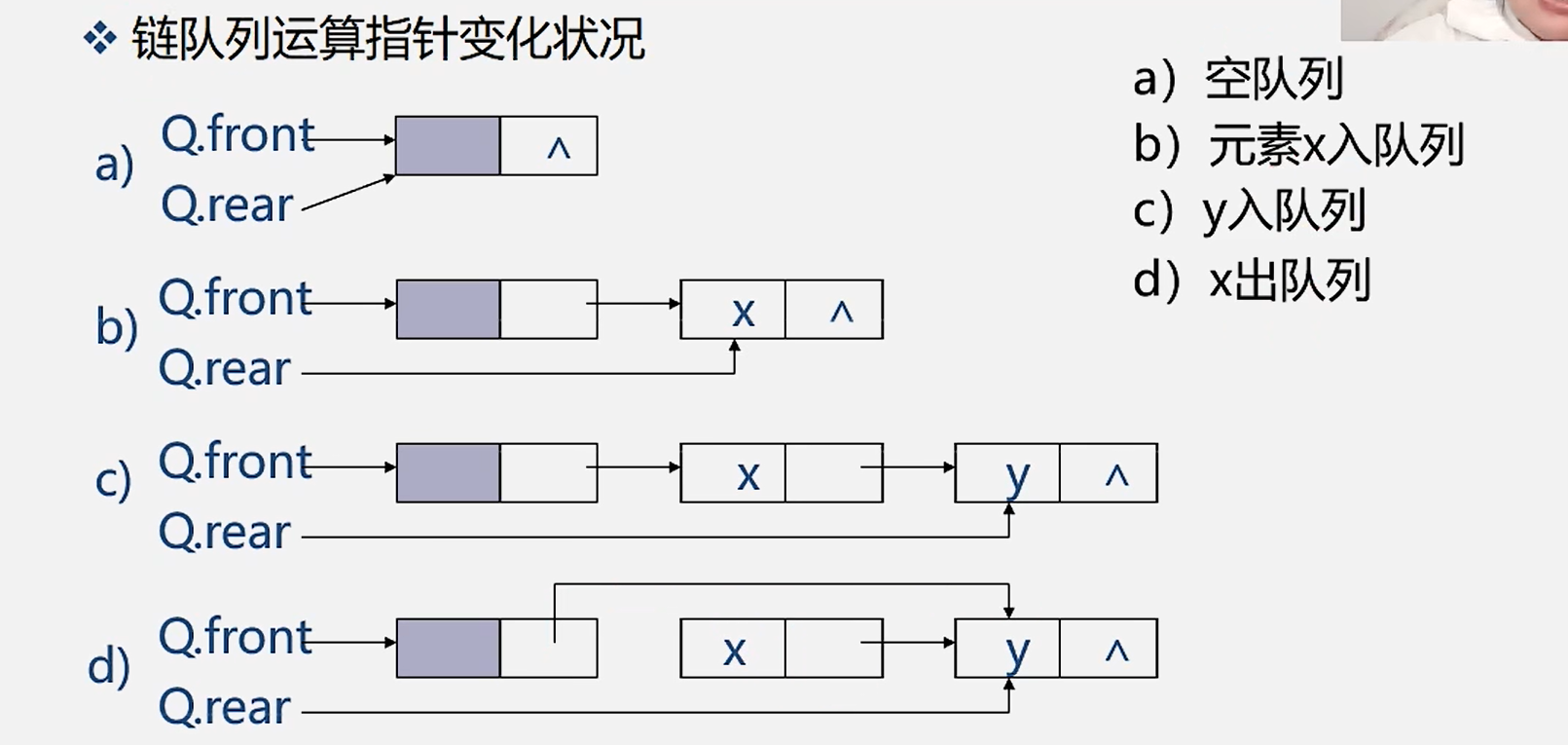
1.链队列运算指针变化状况
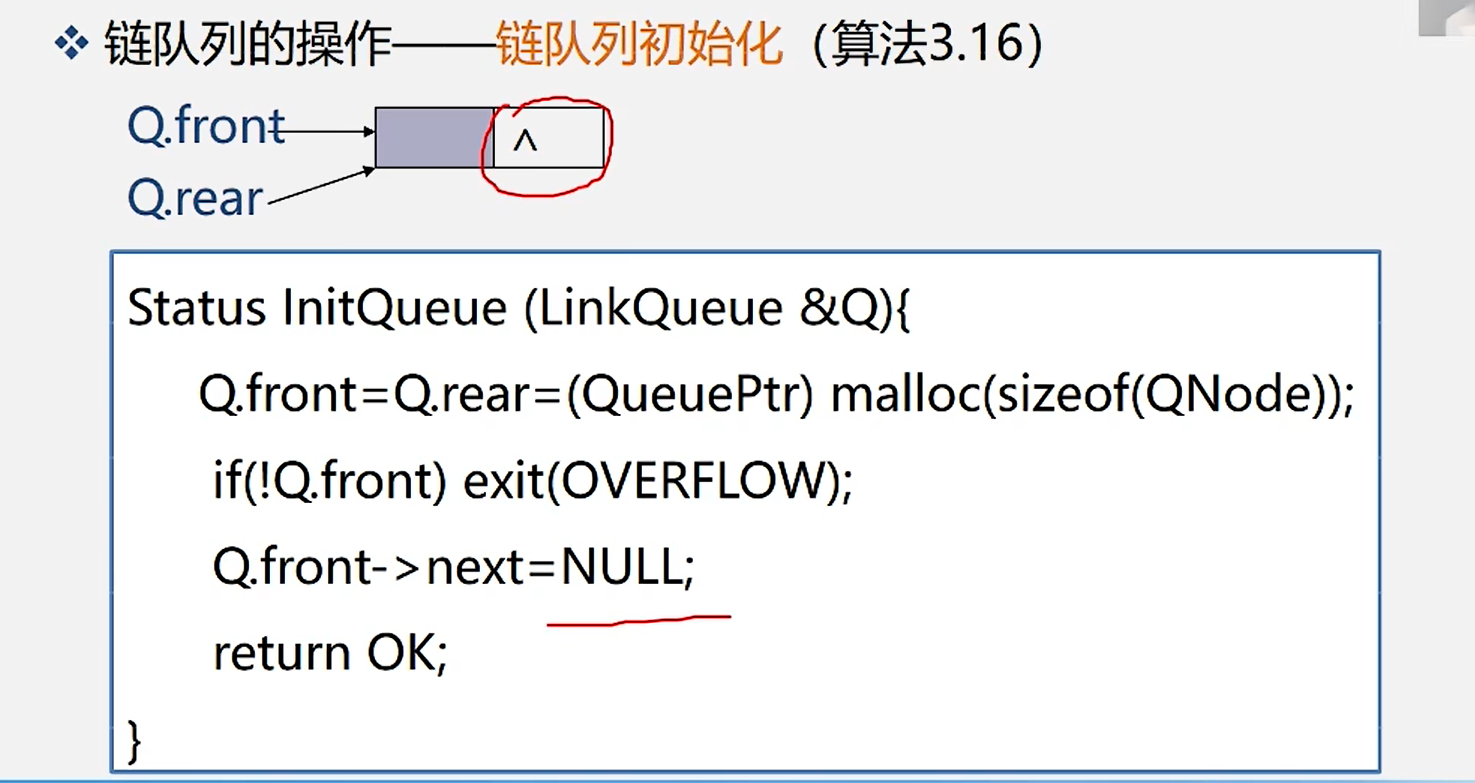
2.链队列初始化
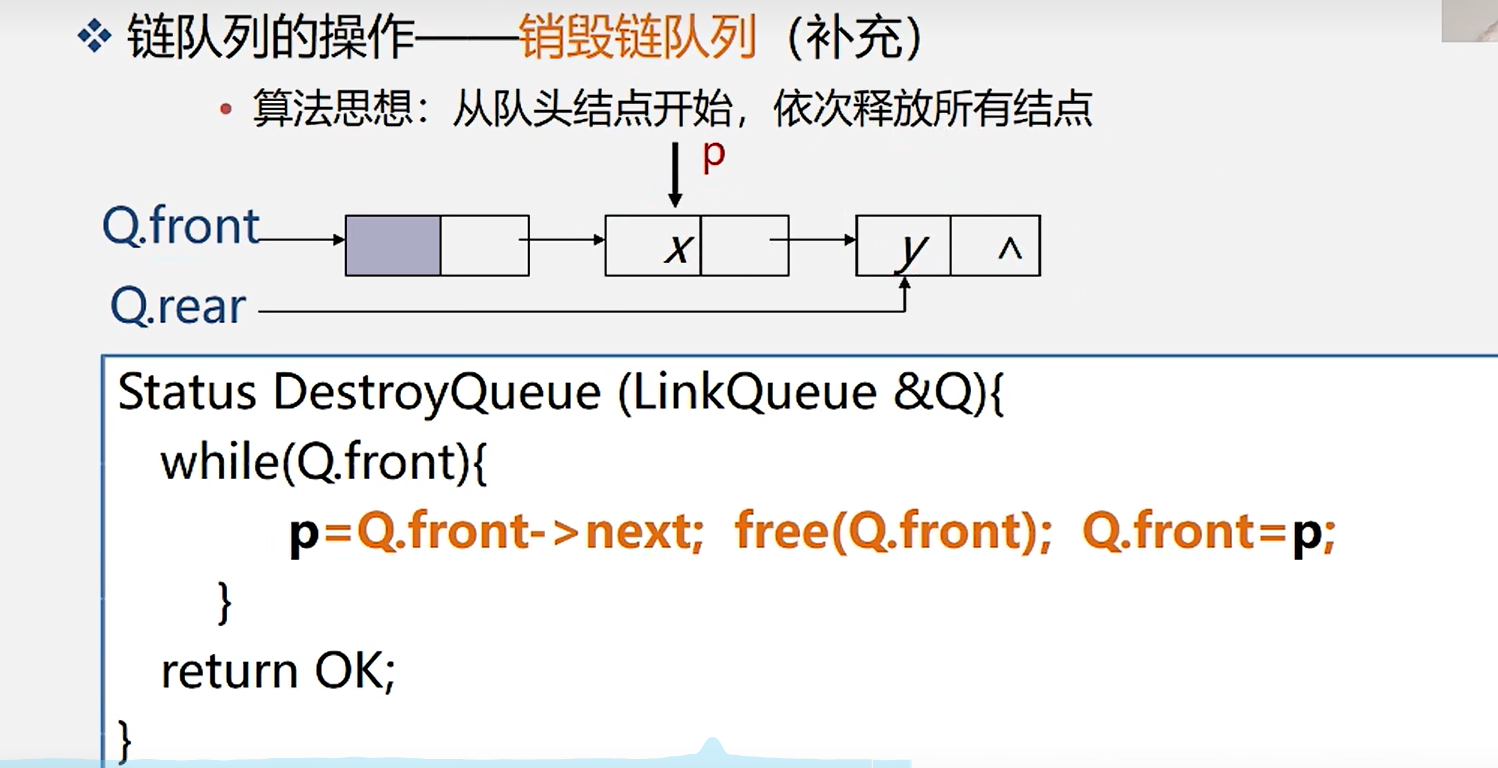
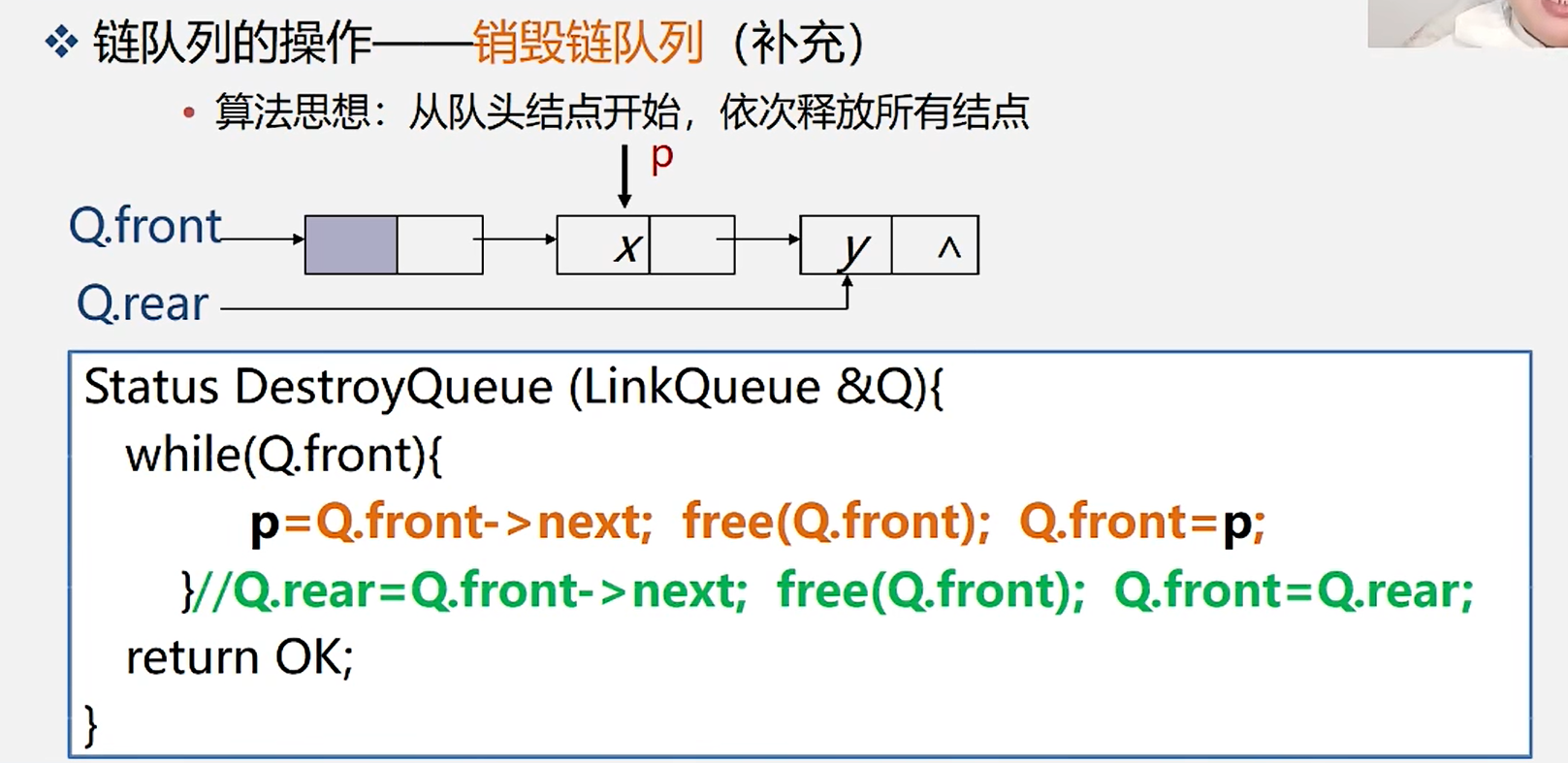
3.销毁链队列
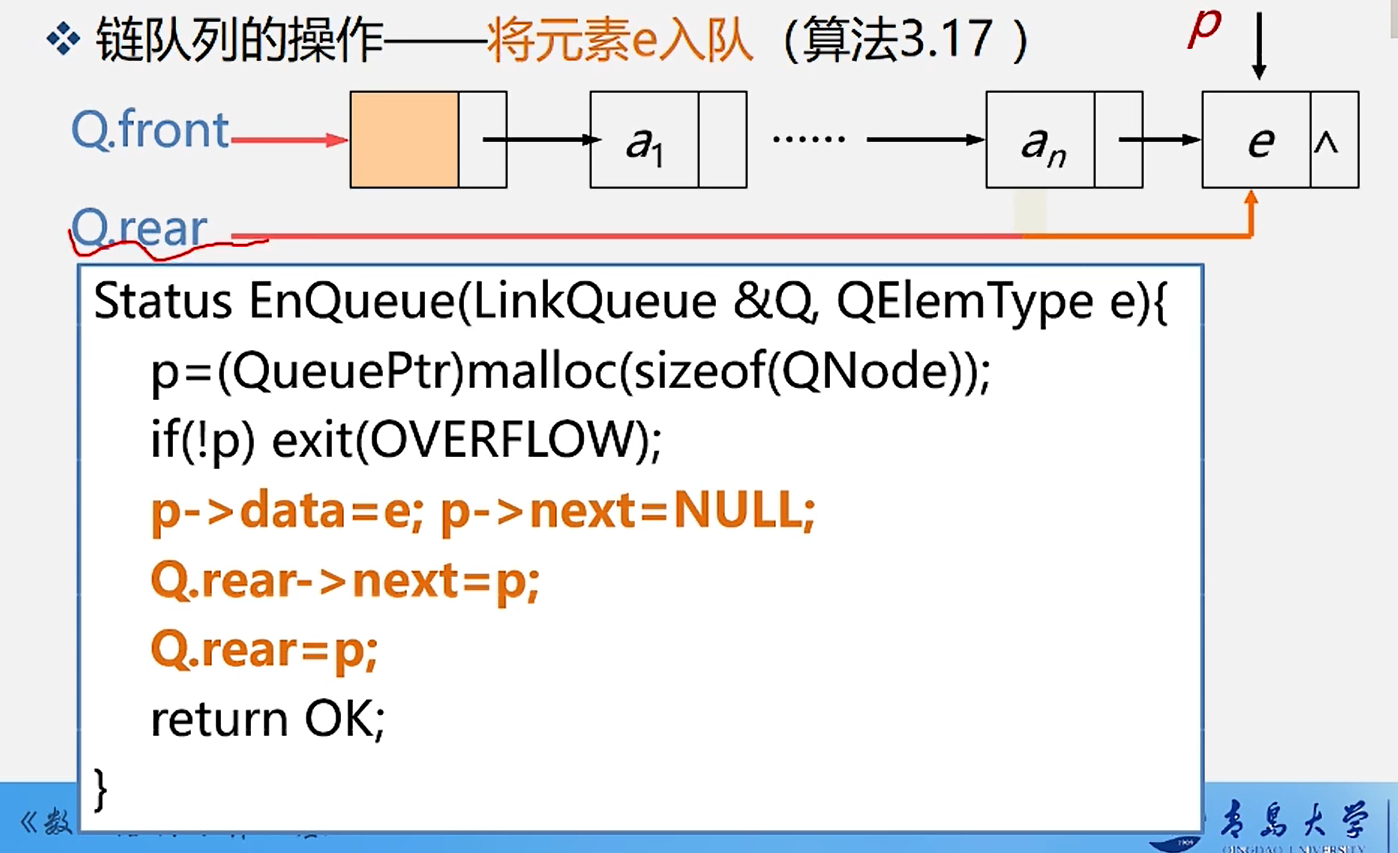
4.将元素e入队
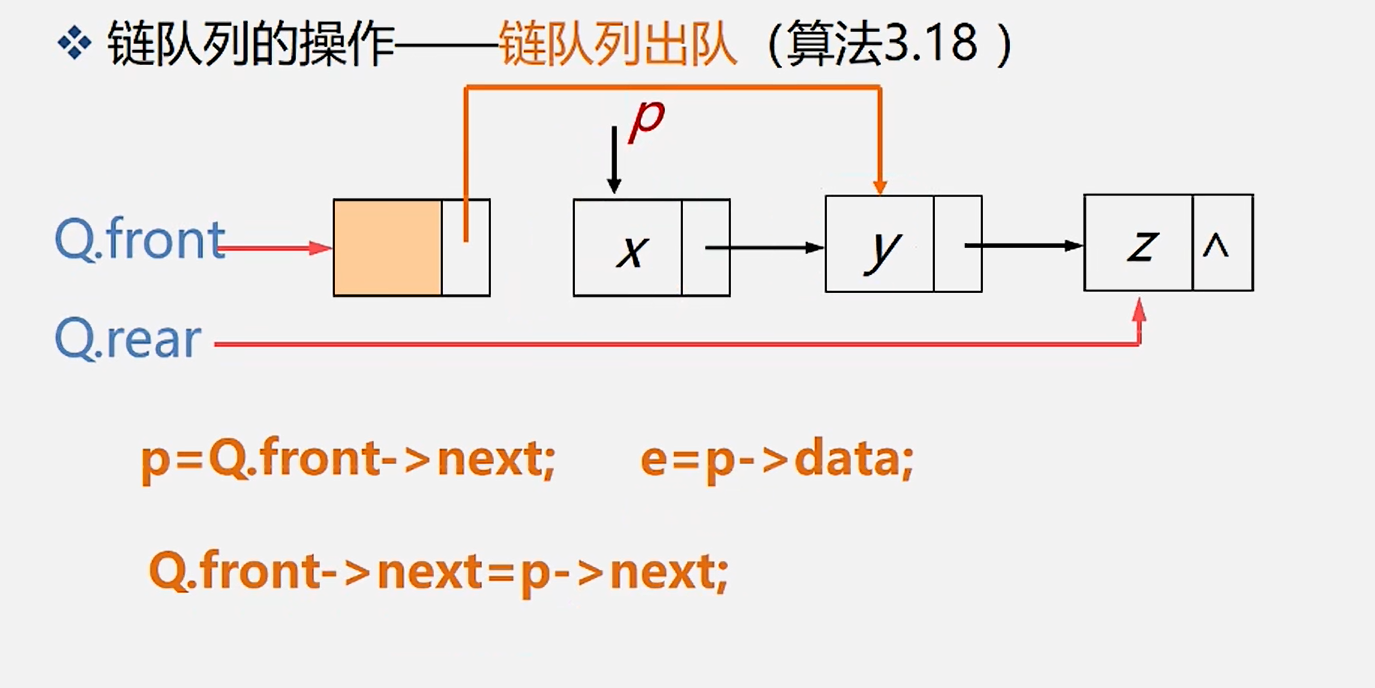
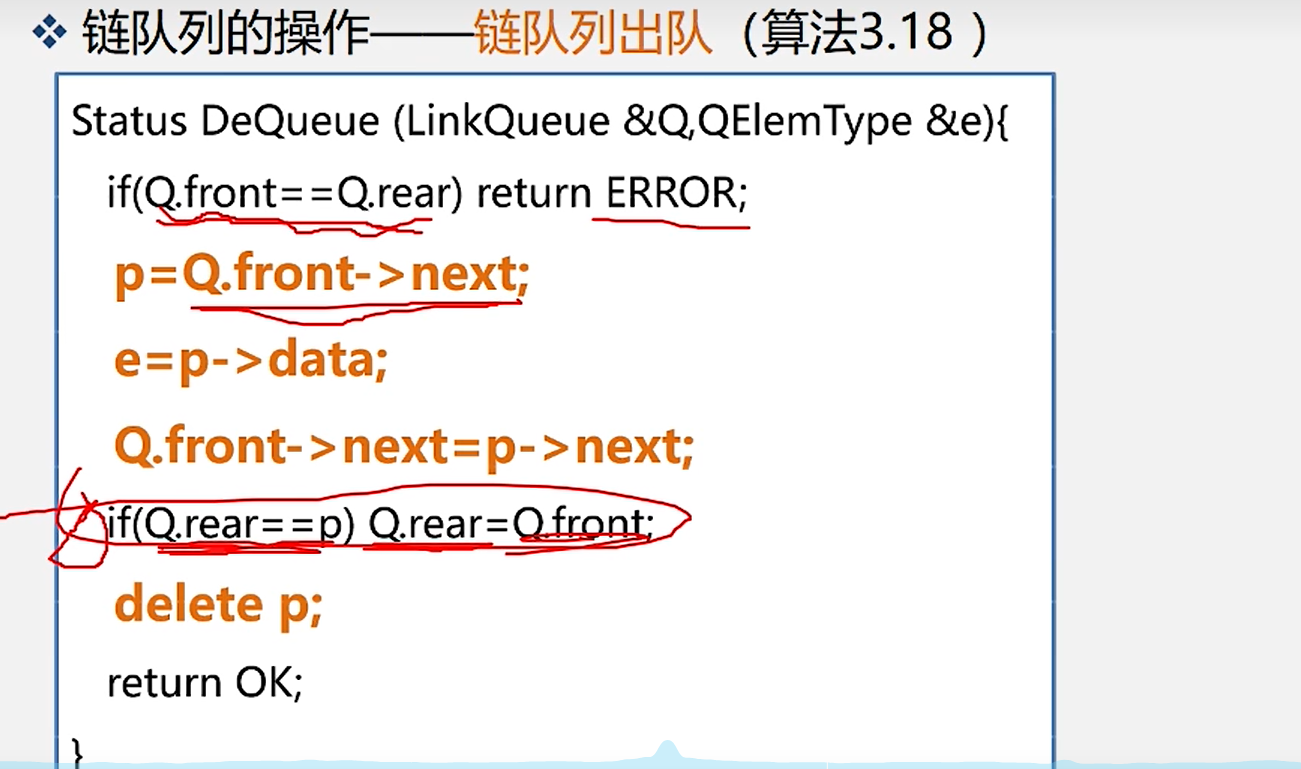
5.链队列出队
6.链队列的队头元素
二.为什么需要栈和队列?(Why)
1.栈的应用

2.队列的应用

三.如何学好栈和队列?(How)
1.chunk it up:指的是把要学习的知识点进行切碎,变成一个有机的整体。
先学底层一个个小知识点,不断积累,一点点串成烤串。(听课)
2.deliberate practicing:做刻意练习,多做题,多实践。
自己练习、梳理、总结(做)
3.feedback:一种是主动式反馈,还有一种叫被动式反馈。
a.主动式反馈:主动去学习,看到别人,原来这个地方可以这么写,这么写之后就特别的漂亮,而且的话程序跑的也很快。(思)
b.被动式反馈:code review。如说这是faker的直播的视角,通过他看,你看他怎么操作,你会知道哦,原来为什么他这么强或者什么?什么地方要学习?(学)
搞清楚,栈、队列的定义,各种操作,扎实基础。
清楚栈、队列的联系与区别。
用心
用心、用心
用心、用心、用心
知其然、知其所以然!!!
多学习,多思考,多总结,多输出,多交流 (five kills)~~~
